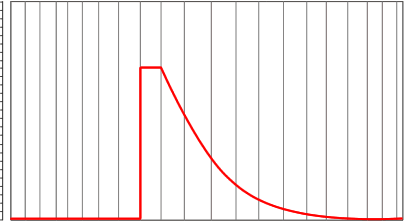
5. ラウドネス計算の基となる考え方
人間が音の大きさを感じかたに影響するものとして、次の3つの現象があります。
1.耳の周波数特性
2.スペクトルマスキング (周波数軸上で起こる現象)
3.テンポラルマスキング (時間軸上で起こる現象)
ラウドネスの計算をする場合、この3つの現象を考慮する必要があります。
5-1 等ラウドネス曲線(純音)
ラウドネスの計算に重要となる要素のひとつが聴覚の周波数特性です。純音に対する等ラウドネス曲線を下に図示しましたが、それを見ていただくと、橙色で示した2 kHz から4 kHzで感度が良く、低音で感度が悪くなる特性を持つことが分かります。
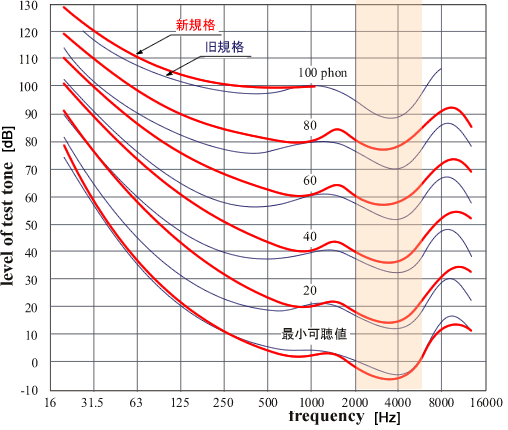
また、この特性は音圧によって異なります。上側データの高い音圧の場合には比較的平坦な特性となり、下側データの音圧が低い場合には低音における感度がより小さくなります。 人間の聴覚の周波数特性はとても複雑です。ラウドネスの計算では、このような複雑な特性が考慮されて います。 ちなみに、A 特性カーブは、聴覚の周波数特性と似た特性のフィルターを使用しています。ただし、中くらいの音圧の場合の等ラウドネス曲線(図中、40 phon の曲線)に相当するフィルターを使用しているため、 人間が聞いたときの音の大きさとは異なる場合があるのです。
5-2 スペクトルマスキング(Spectrum Masking)
スペクトルマスキングの影響もラウドネスの重要な要素です。マスキングとは、ある音が聞こえているときにもう一つの音を聞かせると、2 番目の音は 1 番目の音によってかき消され(マスクされ)聞こえなくなってしまう現象です。
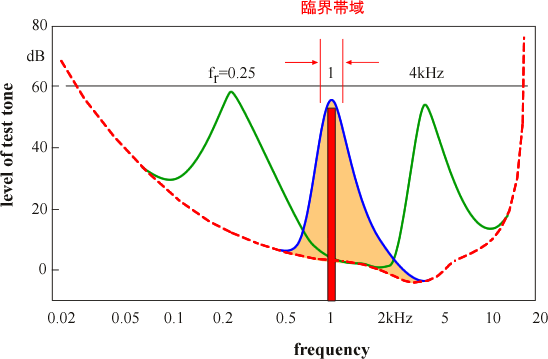
今、1kHz の狭帯域雑音を聞いているとします。この時、上のグラフ中の影をつけた範囲は、1 kHz の狭帯域雑音によってマスクされています。 この範囲に新たに音が加わったとしても音の大きさは増えません。また音によっては完全にかき消されて聞こえない場合もあります。
スペクトルマスキングのカーブの形は周波数によって異なります。また、音圧が異なるとカーブの形が異なります。スペクトルマスキングは非線型で複雑な現象です。 また、マスキングによって生じるカーブはバンドバスフィルターのような形をしています。このフィルターの通過帯域幅に相当する範囲を、臨界帯域(単位:Bark)と呼びます。
スペクトルマスキングが起こる理由は、耳の構造にあります。次図は耳の構造を示したものです。耳かいから入った音は外耳道を通り、鼓膜、耳小骨を振動させて蝸牛に至ります。 蝸牛は音の周波数分解を簡単に行っている器官で、管状をしており、それがカタツムリの殻のようなぐるぐると巻いた形をしています。
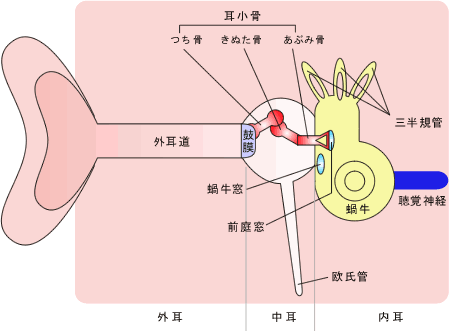
この渦巻き管をひきのばし、その断面を示したのが次の図(影部分)です。
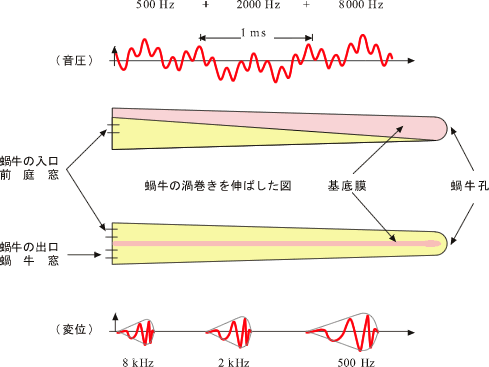
蝸牛内部は基底膜という膜で上下2つに分けられています。蝸牛に到達した振動はこの膜を振動させながら蝸牛入口(左側)から奥(右側)へ進み、基底膜上にある神経細胞を興奮させます。このときある特定部分の基底膜が特に大きく振動をします。大きく振動する部分は入ってくる音の周波数によって異なり、高い周波数の音の場合には入口付近で、低い場合には奥のほうで大きな振幅となります。したがって音の周波数が異なれば興奮する神経も異なり、このために高い音か低い音かを感じることができるのです。 基底膜は膜上の、ある1点のみが振動するわけではなく、幅を持って振動します。そのため、例えば 1 kHz の音を聞いたとしてもそのまわりの周波数に対応する神経も興奮します。 この時にさらに 1 kHz よりも少しだけ高い周波数の音を聞いたとしても、すでに興奮している神経細胞はさらに興奮することはできず、音の大きさはさほど変わったようには聞こえません。これがスペクトルマスキングの現象です。
5-3 スペクトルマスキングと音の大きさ
スペクトルマスキングと、音の大きさの関係を理解するために、マスキングカーブを単純化したモデルで説明します。
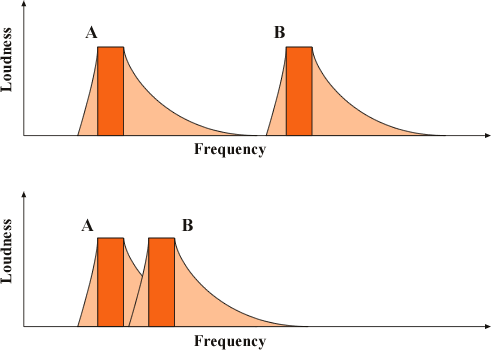
前のページの上の図は、A と B の2つの音が周波数軸上で、離れている場合です。四角い部分がそれぞれの音で薄く影をつけた部分がマスキングされている部分です。 音の大きさ(ラウドネス)は、これらの面積に比例するので、A のみが存在する場合よりも、B が追加された場合には約2倍の大きさに感じます。 一方、下の図は2つの音の周波数が近い場合です。2つの音によってマスキングされた部分は重なっています。その結果、B が加わっても面積は A のみが存在する場合とさほど変わらず、 音の大きさは少し増えるのみです。これらの音のエネルギは、上の図も下の図もどちらも2倍ですから音圧レベルで比較すると、同じ値となってしまいます。
5-4 ラウドネス計算用チャート
これらの現象を考慮して音の大きさを計算するために、ISO 532B ではラウドネスをチャートを使って求めています。
|
A
|
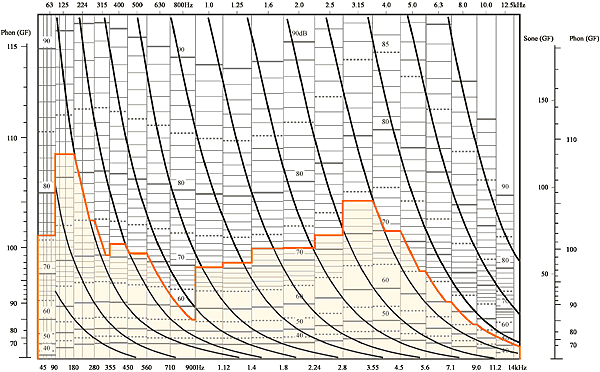
周波数マスキングを模擬するためには、上図 A のようなモデルを用います。 周波数マスキングカーブはその音よりも高い周波数に向かうカーブのほうが低い周波数に向かうカーブよりも傾きが緩やかで周囲に及ぼす影響が大きいため、 上側のカーブのみを考慮しています。 ラウドネスを求めるには、まず 1/3 オクターブ分析を行い、 その結果を、図のようなチャートに書き込みます。描かれたカーブの下方の面積を計算し、面積に対応するラウドネスを読み取ります。 音圧や音場の状況に応じて ISO 532B では 10種類のチャートを用意しています。適したチャートを使用してラウドネスを求めます。
5-5 臨界帯域幅
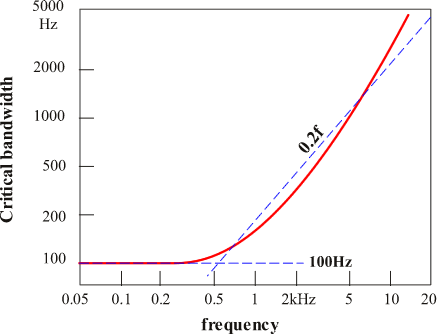
5.4 のチャートでは、これまでに述べた、聴覚の周波数特性、スペクトルマスキングが考慮されています。 ここで、もうひとつ考慮するべきなのは、聴覚の周波数分解能です。聴覚の周波数分解能はほぼ 1/3 オクターブバンド幅に一致しています(音の大きさを議論する場合です。 音の高さの分解能はもっと細かくなります)。 ところが、500 Hz よりも低い音域では、1/3 オクターブよりも幅が大きく、分解能は粗くなります。 そこで、ISO 532B の方法では、低域のバンドは聴覚の分解能に応じてバンド幅をひろげるために足し合わせを行っています。 ISO のチャートで、低域の縦線の間隔が狭くなり、4バンドや 3バンドまとまって描かれているのはそのためです。
5-6 時間マスキング
ラウドネスのもう一つの重要な要素となるのはテンポラルマスキングです(時間マスキング、経時マスキングとも言います) 。 これは時間軸上で起こるマスキングのことです。
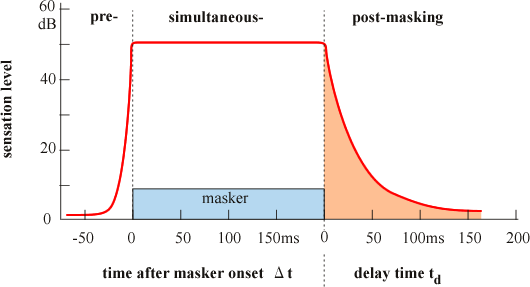
例えば、ある音が鳴り止んだ直後に別の音を短く鳴らした場合、後の音が前の音に掻き消されて聞こえなくなってしまう現象です。 これははじめの音を聞いているときの耳の中の膜の振動がすぐに止まらずに、徐々に減衰する為です。 また膜に接している神経の興奮も徐々に小さくなっていきます。興奮が充分に減衰する前に次の音が鳴ったとしてもその音は聞こえません。
ところで ISO で規格化されているラウドネスの計算方法には、このテンポラルマスキングの影響が考慮されていません。 したがって ISO の方法によるラウドネスでは定常音の評価しか行うことができません。
5-7 小野測器の音質評価システム
小野測器の音質評価システムは、ISO 532B に基づいた方法でラウドネスを計算しています。ただし、ISO では時間的に変動する音に付いては評価できないため、 ISO の方法に加えてテンポラルマスキング(ポストマスキング)の影響も計算に組み入れています。なお、計算結果は 2 ms ごとに算出されます。

5-8 ラウドネスの基準
ラウドネスの基準となる音は、音圧レベル 40 dB で周波数 1 kHz の純音です。この時、1 sone となります (ラウドネスレベルは 40 phon)。
この音と同じ大きさに聞こえる音は 1 sone、2倍の大きさに聞こえる音は 2 sone となります。