5. デシベル値の計算
これまで説明してきましたように、デシベル値に関しては相対レベル値と絶対レベル値があります。これらの加算や減算はどうしたらよいのでしょうか?
以下の組み合わせが考えられます。
(1) 相対レベル値と相対レベル値
この場合は、単純にデシベル値の加算や減算が可能です。
|
[例] A dB のアンプと B dB のアンプを接続した時の合成の増幅率は( A + B )dB となる。 |
(2) 絶対レベル値と相対レベル値
この場合も、デシベル値の数値的な加算や減算が可能です
|
[例] 感度が −30 dB(re. 1 V/Pa)のマイクロホンに、挿入損失 −2 dB のプリアンプをつけて、1 Pa の音圧(音圧レベル 94 dB )を測定すると、−32 dBV (約 25 mV )の電圧が出力される。 |
(3) 絶対レベル値と絶対レベル値
この場合は、単純にデシベル値の数値的な加減算は出来ません。電気系・音響振動系にかかわらず、パワー値での加減算が必要になります。すなわち、デシベル値を真数に戻して、真数で加減算を実行し、その後にデシベル値に変換します。このような加算をエネルギー加算(パワー加算、デシベル和算)などと呼びます。
例えば、L1 dB と L2 dB との絶対レベル値の加算値(あるいは減算値)L dB は;
と計算できます。
ただ、絶対レベル値同士の加算はあまり意味を持ちませんが、減算は真数の比に相当しますので、同じ基準値を持つ絶対デシベルの差は相対デシベル値として意味を持つことになります。例えば、建物の音響性能においてよく使われる室間音圧レベル差 D は以下のようにデシベルの差として求められます。

|
[例] 60 dB と
63 dB との合成の音圧レベル値は、(5-1)式に代入して;
暗騒音が
40 dB 下で測定したら音圧レベルが
45 dB
であった。この時の暗騒音を補正した音圧レベルは、(5-1)式に代入して;
1/3 オクターブバンドフィルター分析で、800 Hz で 72 dB、1 kHz で 76 dB、1.25 kHz で 74 dBのとき、バンド合成により、中心周波数 1 kHz の 1/1オクターブバンドフィルター分析のレベルは;
|
【注意】
絶対レベル値の平均も真数上で加算して平均をとる方式を用います。このような平均をエネルギー平均(パワー平均、デシベル平均)と呼びます。例えば、音圧レベル L1 dB、L2 dB、L3 dB の平均音圧レベル L dB は;
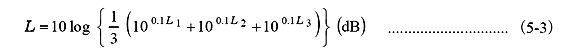
例えば、80 dB 、82 dB 、84 dB の平均レベルは、(5-3)式に代入して、82.3 dB となります。ただし、既存の規格によっては、デシベル値の数値平均で求める場合もあります。この方式をデシベル値の算術平均と呼ぶことがあります。この例では;

82 dB となります。なお、デシベル値の計算に関しては、小野測器ホームページ「騒音計とは」の“12章 デシベル(dB)についての計算”もご参照ください。
参考文献
1) 伊藤健一著「デシベルのはなし」日刊工業新聞社
2) 酒井洋・鈴木秀策著「デシベル−伝送量の扱い方−」日刊工業新聞社
3) 久野和宏著「dB考」日本音響学会騒音・振動研究部会
4) 松浦裕之「dBいろいろ」日経エレクトロニクス(1988. 11. 28)
5) 小野測器ホームページ技術資料「騒音計とは」