25. 換算周波数ノモグラム
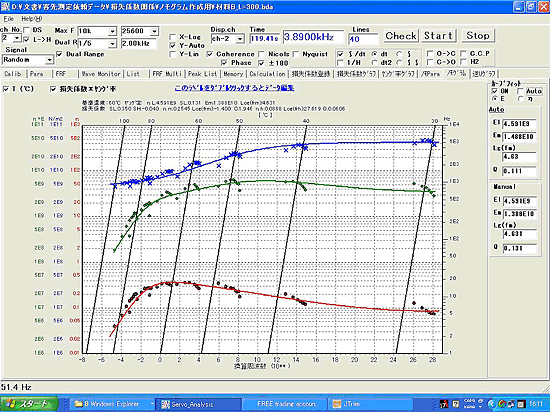
様々な温度、周波数における複素弾性係数の測定値を、横軸(対数)に換算周波数 fr 、左縦軸に複素弾性係数をとった合成曲線として整理しておく。次に、同じ図中に代表的な温度・・、T-2、T-1、T0、T1、T2、・・・におけるシフトファクター αT を比例係数とする直線( fr = αT・f )を、横軸に換算周波数 fr 、右縦軸に周波数 f をとって描くことにより、任意の温度[T]と周波数[f]における複素弾性係数と損失係数の値を合成曲線から直接読み取ることができる。 このようにして整理された図を換算周波数ノモグラムと呼ぶ。換算周波数ノモグラムは、国際規格である ISO 10112 において、制振材料の複素弾性率のグラフ表示として推奨されている。
|
図4 換算周波数ノモグラムの一例 |
1. 換算周波数ノモグラムの作成
(1) 基材の影響の除去:
制振材料を片面に貼った2層型梁などでは、測定した損失係数は制振材と基材からなる複合体としての特性となる。ノモグラム解析に必要な材料単体の特性(損失係数、弾性率) は梁の理論である“RKU 基礎方程式”(ヤング率等の計算参照)によって基材の影響を計算上取り除く。
(2) 温度 - 周波数換算則の適用:
制振材料の制振特性(動特性)は温度と周波数の両方に依存するため、弾性率や損失係数をこの両パラメーターについて表わそうとすると3次元表示が必要となる。ここで重要なのが温度
- 周波数換算則である。温度 -
周波数換算則は粘弾性材料(特にガラス転移領域)において良く成立し、温度の変化を周波数の変化に置き換える(換算周波数)ことによって、制振材料の動特性を2次元で表現することができる。
基準温度 T0 をガラス転移温度 Tg にとると、WLF式(1式)はほぼ C1
= 17.44、 C2 = 51.6 となる。 WLFは非晶性高分子に対してよく成立する。一方、結晶性分子やフィラーが入ると誤差が増し、ガラス転移温度
Tg 以下では誤差が大きいといわれている。
(3) マスターカーブ(合成曲線):
温度 - 周波数換算則を適用し、複数の温度データを連続した1本のマスターカーブに合成する。換算周波数ノモグラムは、こうして得られた制振材料単体の損失係数とヤング率を換算周波数軸上にプロットすれば完成する。また、この複雑な特性を取扱い易くする目的で、あらかじめ 用意した粘弾性特性のモデル式にカーブフィットさせ、粘弾性特性を幾つかのパラメーターで表すことも行われている。
2. ノモグラムの作成手順
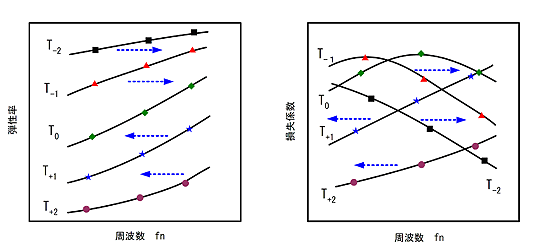
前述の RKU式を使って求めた制振特性単体の特定の温度(T-2 〜 T+2 )における弾性率(ヤング率)を図5 に、損失係数を図6 に一例として示す。
|
|
|
|
図5 周波数 対 弾性率 |
図6 周波数 対 損失係数 |
|
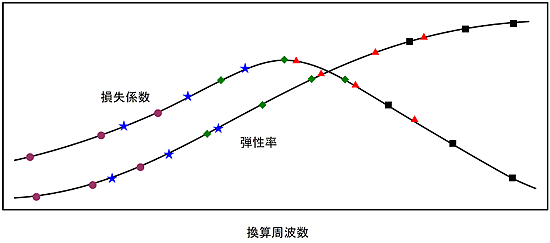
図7 換算周波数 対 弾性率・損失係数 |
ここで、図5、6 に示す粘弾性材料の対温度挙動を考慮する。この図からガラス転移温度を適切に推定し、温度 - 周波数換算側の基準温度 ( T0 ) を Tg の近傍として、以下により決定する。
-
特定の温度 T1 (試験片の一個の測定温度)を決める。
-
αT を計算する。
-
実験で測定した試験片(温度が T1 の場合)の共振周波数と αT を掛け算して換算周波数 fr を計算する。
-
横軸に換算周波数をとり、縦軸に制振材料単体の動特性(損失係数、ヤング率)をとると T1における図7 の一部が得られる。
-
この操作を他の測定温度 T1 や T2 等について繰り返すと、図7が完成する。もしも、この図のデータの並びが滑らかでない場合は、基準温度 T0 を変えて再度、図7を作成して、データプロットが滑らかにつながるまでこの操作を繰り返す。
-
最後に、右側の縦軸に(共振)周波数をとり、上側の横軸に温度をとると換算周波数ノモグラムが完成する。
3. ノモグラム作成時の注意点
ノモグラム作成時には、以下に示すような点を留意する必要がある。
-
対象はオイラーベルヌーイ梁の2層型であるので、試験片の厚み比を大きくしない(3倍以内)。
-
2層型の場合は、せん断(ズリ)変形が発生しないように留意する。
-
計算式には、伸びの影響を考慮していない。
-
鉄やアルミの損失係数は 0.001 より小さいため、基材の損失係数は 0(ゼロ)と仮定している。
-
計算過程で測定誤差や材料誤差の影響が大きくなる。
-
ヤング率を計算する場合に、周波数は2乗で影響する。
-
基材のヤング率を計算する場合、厚みは2乗、長さは4乗で影響する。
なお、換算周波数ノモグラムを求める場合、特に、高温での測定データが使用出来ない場合が多い。この原因は、材料のノモグラムを求める時に、RKU計算式(23.
ヤング率等の計算「2層型複合板の場合」の上式)の
√(平方根)の中が非常に小さくなるか、負になるためである。このため、計算精度を確保するのに、 α![]() 1.1 という判別を設けている。この判定条件により、ノモグラム作成時に測定データを棄却する必要がある。 このため、α の拡大方法(対策方法)の一つとして試験片の損失係数は、できるだけ η > 0.01 となるようにする。
1.1 という判別を設けている。この判定条件により、ノモグラム作成時に測定データを棄却する必要がある。 このため、α の拡大方法(対策方法)の一つとして試験片の損失係数は、できるだけ η > 0.01 となるようにする。
4. 換算周波数ノモグラムの読み方
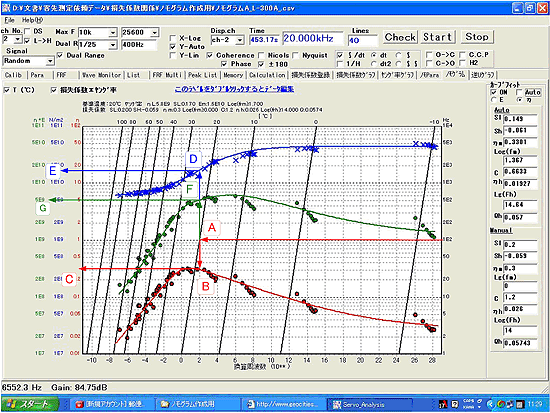
下図8に換算周波数ノモグラムの一例を示す。左側の縦軸は、 損失係数( η、●)と貯蔵弾性率(ヤング率 E’、×)、および損失弾性率 E”、●)を表し、右側の縦軸は、周波数 f を表す。下側の横軸は換算周波数 frで、物理的には意味がないが温度条件を含んだ軸である。上側の横軸は温度(℃)を表す。
|
図8 換算周波数ノモグラム例 |
次に、周波数が 100 Hz で温度 20 ℃ における制振材料単体の損失係数とヤング率を求める手順を示す。
-
右側の縦軸(周波数軸)の 100 Hz のラインを横に見る。
-
このラインと、上側の横軸(温度軸)の温度が 20 ℃ の斜め線との交点 A を求める。
-
交点 A から垂線を引いて、損失係数のカーブフィットラインとの交点 B を横に水平に移動、損失係数軸の値 C を読むと約 η = 0.3 を得る。
-
交点 A から垂線を引いて、ヤング率のカーブフィットラインとの交点 D を横に水平に移動、ヤング率軸の値 E を読むと約 E’ = 1.8E10(N/m2) を得る。
-
交点 A から垂線を引いて、損失弾性率のカーブフィットラインとの交点 F を横に水平に移動、損失弾性率軸の値 G を読むと約 E″= 5.2E9(N/m2)を得る。