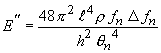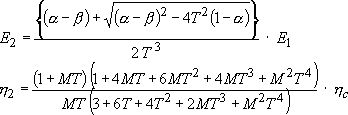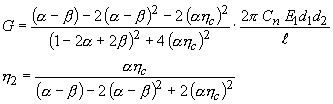22. 損失係数測定の際使用する窓関数について
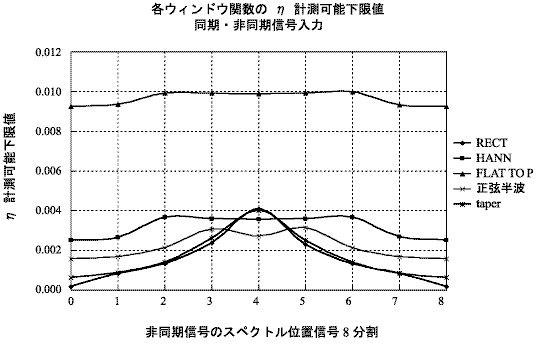
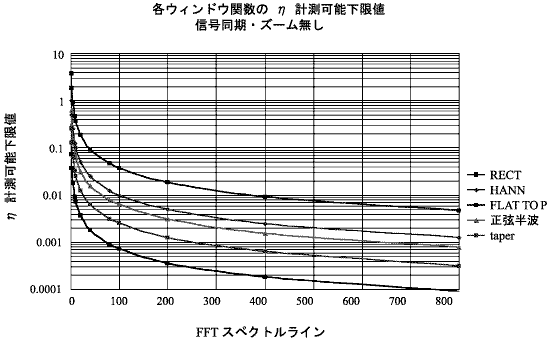
窓関数によって損失係数測定の際に、周波数応答関数が変形すると予想される。 下図は各窓関数をかけたときの損失係数の測定下限値を示す。
|
|
前図から次のことがいえる
-
FLAT-TOP ウインドウは損失係数測定には向いていない。
-
方形波ウインドウがワーストケースの分解能と分解能の中央位置に信号が入力された場合を除いて、損失係数測定には最適である。
-
従来「信号が非同期の場合には、ウィンドウ関数はハニングを使え」と言われてきたが、損失係数測定時（ピークから -13 dB よりも大きな値で η を求める場合）に限り、方形波ウインドウが最も小さな損失係数まで精度良く測定できる。ただし、矩形窓を使用してコヒレンスが低下する場合は、テーパー窓を使用する。
-
共振点が FFT 画面の左側に近づけば近づくほど、ウインドウ関数の影響が大きい。例として、ズームを使用しないでハニングウインドウ使用の場合の、FFT 10ライン目の測定下限は η＝ 0.15 である。
-
周波数応答関数波形の山が画面の左側にあるということは、低い周波数の共振・反共振を 高い周波数レンジで測定したことであり、山を右側に移動するということは（1）周波数レンジを下げる。（2）周波数ズームを行うことであるから、ここでもズーム分析の必要性が確認された。
-
ズーム分析の別の効用として、ズーム分析は時間フレームを長くすることなので、インパルスレスポンスのはみ出し変形も減少する。さらに、ズーム分析は周波数分解能を上げることになるため、この部分での誤差の減少も期待できる。また、FFT 点数を増やすことによっても同様の効果があると考えられる。 最近では 65,536 点の FFT で 25,600 ラインのスペクトルを計算するものまで出現して、ある程度損失係数が大きい（η：0.01 程度）場合にはズーム分析が不要なものが使いやすい。
23. ヤング率等の計算
無垢材料の測定からヤング率を求める計算式、および RKU (Ross, Kerwin, Unger)方程式を用いた複合型（2層型・3層型）で測定した損失係数・ヤング率から制振材単品の損失係数・ヤング率を求める計算式を示す。
■ 無垢材料
共振周波数を fn (Hz)、半値幅を Δ fn (Hz)、試料片の長さを
(m)、試料片の厚さ
ｈ (m)、試料片の平均密度を ρ (kg/m3) とすると。
 |
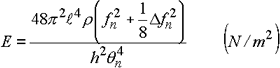ダンピングが小さい場合は 1/8 Δ fn2 を無視し
|
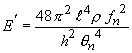
また、損失係数 η は
 |
ここで
- 片持ち梁法と中央加振法反共振使用の場合
| 次数 n | θn | θn4 |
|---|---|---|
| 1 | 1.87510 | 12.36 |
| 2 | 4.69409 | 485.5 |
| 3 | 7.85476 | 3806.6 |
| 4 | 10.99554 | 14617.3 |
| 5 | 14.13717 | 39943.8 |
| 6 | 17.27876 | 89135.4 |
| 7 | 20.42035 | 173881.2 |
| 8 | 23.56194 | 308208.2 |
|
以下 + π |
||
| ただし、片持ち梁法の場合は（１）式の
に全長からつかみしろを除いた長さを入力。中央加振反共振を使用する場合は（１）式の
に /2を入力する。 |
||
- 中央加振で共振を使用する場合は共振周波数を求めて、θ n に下記値を使用する。
| 次数 n | θn | θn4 |
|---|---|---|
| 1 | 4.73004 | 500.56 |
| 2 | 10.99561 | 14617.6 |
| 3 | 17.27876 | 89135.4 |
| 4 | 23.56194 | 308208.2 |
| 5 | 29.84513 | 793403.1 |
| 6 | 36.12831 | 1703690.0 |
| 7 | 42.41150 | 3235448.8 |
| 8 | 48.69468 | 5622456.0 |
|
以下 + π |
||
|
は、全長を入力 |
||
- 両端自由で２点吊り（支持）法の場合
| 次数 n | θn | θn4 |
|---|---|---|
| 1 | 4.73004 | 500.56 |
| 2 | 7.85320 | 3803.5 |
| 3 | 10.99561 | 14617.6 |
| 4 | 14.13717 | 33943.8 |
| 5 | 17.27876 | 89135.4 |
| 6 | 20.42035 | 173881.2 |
| 7 | 23.56194 | 308208.2 |
|
以下 + π |
||
|
は、全長を入力 |
||
また高次では θn+1 と θn の差はほとんど π と一致することから
 |
となり次数のファクター θn および密度 ρ が消去されたこの式が、次数がわからない場合に有用な式である。
■ ２層型複合板の場合
| 複合試験片の損失係数： η c
共振周波数：ｆc［Hz］ 自由長の長さ： 基材の損失係数： η1 ＝ 0 と置く 共振周波数：ｆi［Hz］ 厚み：ｄ1［m］ 密度：ρ 1［kg/m3］ ヤング率：Ｅ1［N/m2］ 制振材単品の損失係数： η 2 厚み：ｄ2［m］ 密度：ρ 2［kg/m3］ ヤング率：Ｅ2 ［N/m2］ |
|
さらにヤング率比 E2 / E1 ＝ M、厚み比 d2 / d1 ＝ T、密度比 ρ2 / ρ 1 ＝ D と置くと、制振材単品の損失係数およびヤング率は、基材自身のデータと複合試験片のデータから次式により計算できる。
|
|
ただし、ここで
 |
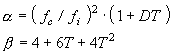である。
ただし、α ≧ 1.1 の時に成り立つ。
■ 両面貼り複合板（上下同一制振材使用）
| 複合試験片の損失係数： η c
共振周波数：ｆc［Hz］ 自由長の長さ： 基材の損失係数： η1 ＝ 0 と置く 共振周波数：ｆi［Hz］ 厚み：ｄ1［m］ 密度：ρ 1［kg/m3］ ヤング率：Ｅ1［N/m2］ 制振材単品の損失係数： η 2 厚み：ｄ2［m］ 密度：ρ 2［kg/m3］ ヤング率：Ｅ2 ［N/m2］ |
|
さらに厚み比 d2 / d1 ＝ T、密度比 ρ2 / ρ1 ＝ D と置くと、制振材単品の損失係数およびヤング率は、基材自身のデータと複合試験片のデータから次式により計算できる。
 |
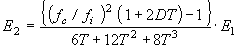ここで、
と書いて
 |
ただし、ここで
 |
の時に成り立つ。
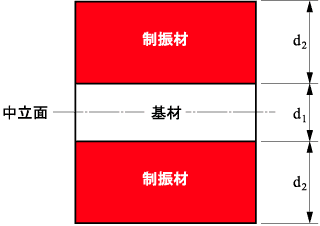
■ サンドイッチ型複合板（制振鋼板）の剪断弾性率と損失係数
| 複合試験片の損失係数： η c
共振周波数：ｆc［Hz］ 自由長の長さ： 基材の損失係数： η1 ＝ 0 と置く 共振周波数：ｆi［Hz］ 厚み：ｄ1［m］ 密度：ρ 1［kg/m3］ ヤング率：Ｅ1［N/m2］ 制振材単品の損失係数： η 2 厚み：ｄ2［m］ 密度：ρ 2［kg/m3］ 剪断弾性率： Ｇ［N/m2］ |
|
さらに厚み比 ｄ2 / ｄ1 ＝ T、密度比 ρ2 / ρ1 ＝ D と置くと、制振材単品の損失係数および剪弾性率は、基材自身のデータと複合試験片のデータから次式により計算できる。
|
|
ここで
 |
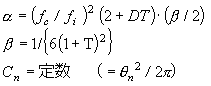ただし
 |
の時に限る。