24. 粘弾性材料の物理特性
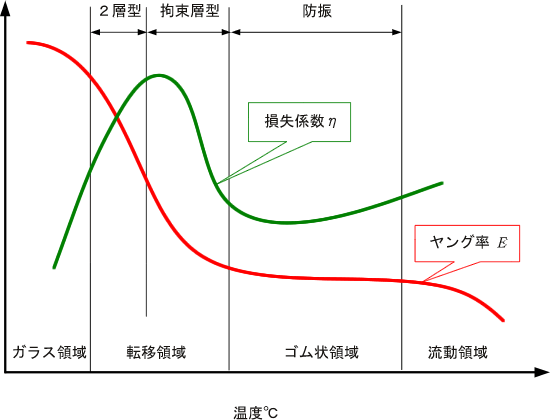
高分子材料は各々の分子鎖がランダムに絡み合いながら結晶部と非晶部が混在した状態で存在しており、温度・周波数依存性は分子の粘弾性に依存する。これらの材料の分子鎖はさまざまな運動モードを有しており、モードごとに特定の温度、特定の周波数でエネルギーを解放する。 制振性能はこの分子運動が活発になる転移領域で最大となる.ガラス領域での材料分子の主鎖の局所的運動は、転移領域では主鎖のミクロブラウン運動に変わり、これにより最も大きな損失を与える。また温度 - 周波数換算式である、W.L.F. (Williams、Landel、Ferry) 式も、この転移領域で成立する。ここで、基礎的な概念として重要なのは、図1 に示す粘弾性材料の弾性率の温度特性をもとに、温度と周波数を入れ換える(温度・周波数換算則:合成曲線 (Master Curve) を使用する)ことにより、周波数に対しても同様な弾性率特性を表すことが出来る点である。
|
図1 粘弾性材料の温度特性 |
1. 温度周波数換算則
制振材料として用いられる高分子材料やゴムなどの粘弾性体の複素弾性係数(縦弾性、横弾性 とも)は、温度 T と周波数 f の関数である。ある温度 T0 を規準温度に設定し、温度 T1 にお ける複素弾性係数を縦軸に、周波数を横軸(対数軸)にとり、これを横軸方向に平行移動すると、基準温度 T0 における複素弾性係数と一致することが知られている。これは、温度を高くすることが周波数を低く(時間を長く)することと対応し、温度を低くすることが周波数を高く(時間を短く)することに対応することを意味している。このように温度の変化を周波数の変化に換算できることを温度周波数換算則と呼ぶ。 制振材料の制振特性(動特性)は温度と周波数の両方に依存するため、弾性率や損失係数をこの両パラメーターについて表わそうとすると3次元表示が必要となる。ここで重要なのが温度- 周波数換算則である。温度 - 周波数換算則は粘弾性材料(特にガラス転移領域)において良く成立し、温度の変化を周波数の変化に置き換える(換算周波数)ことによって、制振材料の動特性を2次元で表現することができる。 このことは、弾性率や損失係数の両特性値に対して、同時に満足するような温度-周波数換算則を見いだすことを意味する。つまり、温度が T だけ変化すると、周波数が f だけ変化したことと等価になるという法則を、広い温度と周波数範囲において、しかも弾性率と損失係数の両方に、同時に適用できるような形で見いだすことになる。 この温度 - 周波数換算則に関する研究は、高分子材料のレオロジーの分野で行われており、もっとも有名なものが、多くの高分子について求めたシフトファクター αT の温度依存性を示した WLF 方程式である。
2. WLF 方程式
シフトファクター αT と温度 T の関係は、様々な粘弾性材料について分析され、Williams-Landel-Ferry(WLF)の式として、次式のように整理されたものが一般に用いられている。
|
|
1式 |
C1 、C2 は定数であり、前項で求めたシフトファクター αT と [ T − T0 ] との関係と一致するように選ぶ。
■ WLF方程式の導出
-
-
非晶質高分子(結晶性ではない)が緩和現象を示すとき、セグメントの動きうる空間、すなわち自由体積がセグメントの移動性、つまり内部粘性を支配していると考えられる。 自由体積概念に基づく Doolittle の粘度式から
-
|
|
2式 |
-
-
自然対数を取って、
-
|
|
3式 |
-
-
これは分子論的立場から粘性率 η と自由体積の関係を示す。f は自由体積分率。 B はほぼ 1 である。このとき、Doolittle の式は以下のようになる。
-
|
|
4式 |
-
-
ここで任意の温度 T における粘性率 ηT と、ガラス転移点 Tg における粘性率 ηTg とを比較する。この二つの温度のおける粘性率は、
-
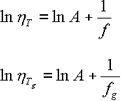 |
5式 |
-
-
ここで f 、fg は T と Tg における自由体積分率である。緩和時間 τ の温度依存性もまた Doolittle 型であると考えると次式のようになる。
-
|
|
6式 |
-
-
次に自由体積分率 f の温度依存性をどのように表すかが問題となる。比容と温度の関係ではガラス状態の熱膨張係数は結晶の場合とあまり変わらないが、Tg 以上になると急増する。 f の温度依存性もおおむねこれと同様であるとすると、
-
|
|
7式 |
-
-
αf は、Tg 以上での自由体積分率差の係数となり、
-
|
|
8式 |
-
-
常用対数変換
-
|
|
9式 |
-
-
この式は、先の WLF 式(式1)と同じ形をしており、係数部を比べることで、WLF 式中の係数 C1および C2 が以下となることがわかる。
-
|
WLF 式
|
(1式) |
|
|
10式 |
|
|
11式 |
|
C1 、C2 : 定数(Constant) |
-
-
換算周波数(Reduced Frequency)fr は、シフトファクターと測定周波数の積で表される。
-
|
|
12式 |
-
-
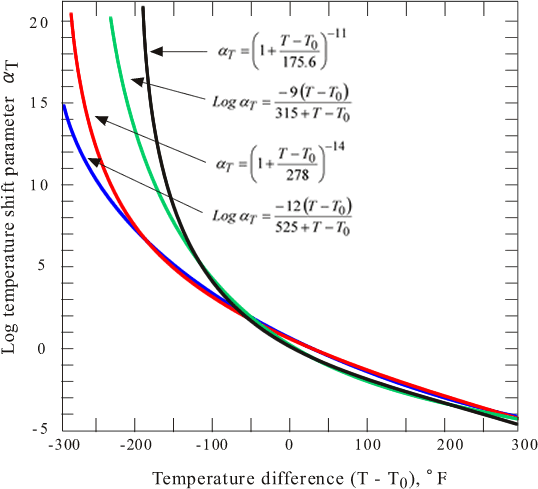
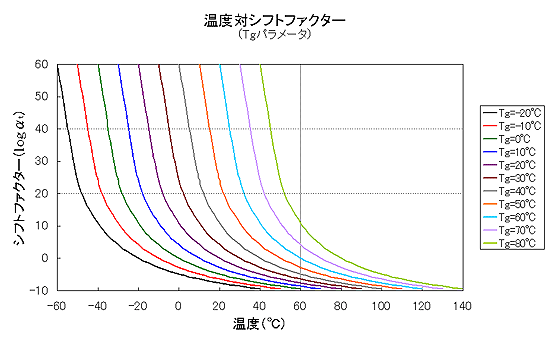
図2にシフトファクター(αT :移動係数)と WLF 式の関係を、図3に WLF 式の C1 = 17.44、C2 = 51.6 とし、Tg をパラメーターにした、温度対シフトファクター(log αT )のグラフを示す。
-
|
図2 合成曲線の比較 |
|
図3 WLF式のシフトパラメーター |