21. 正確な周波数応答関数を得るために
FFT アナライザーを使用する場合の注意事項
- まず始めに減衰法で振幅依存性が無いかどうか検証する。
有る場合は、測定は全て減衰率法で測定する。振幅依存性が有る場合は、周波数応答関数が変形し左右対称にならない場合が多い。 - 加振器への入力信号は同期した sin sweep を最良とする。
FFT の電圧レンジを自動化し、入出力の電圧レンジを最適化し、その電圧レンジ分も周波数応答関数のゲインの計算に反映させる、いわゆるオートレンジ機能があることが望ましい。また、周波数応答関数のゲインによって、信号出力レベルを変える機能があるとなお良い。 - sin sweep で測定に時間がかかる場合には、次図のような特徴を持った信号を使用すると良い。
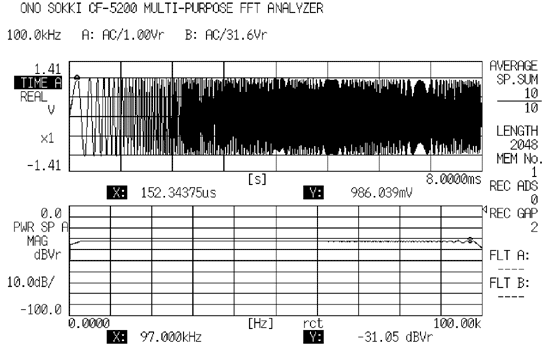
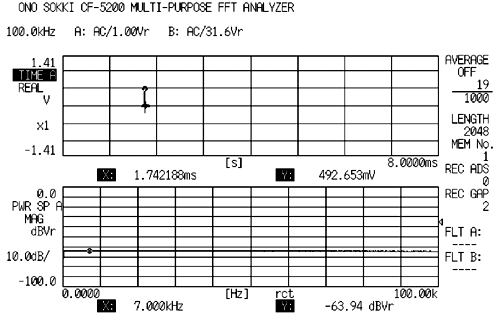
(1) スウェプトサイン信号
|
|
特 徴
-
高速正弦波帚引信号である。クレストファクター(最大値/実効値)は 1.4 と非常に低く、信号の集中する度合いは非常に高い。
-
FFT の解析フレームと同期がとれ、窓関数にレキュタンギュラ窓が使用できるため、リケージエラーが発生しない。
-
常時同じ信号のため、加算の効果はないが、短時間に正確な周波数応答関数の測定が可能のため、近年では多く使用される。
-
周波数ズームで信号同期、帯域制限、分解能変更が行える機器では、見かけ上狭い帯域での制限帚引信号になり、ズーム分析により S/N の向上が期待できる。
次の図は帯域制限したスウェプトサイン信号である。
|
|
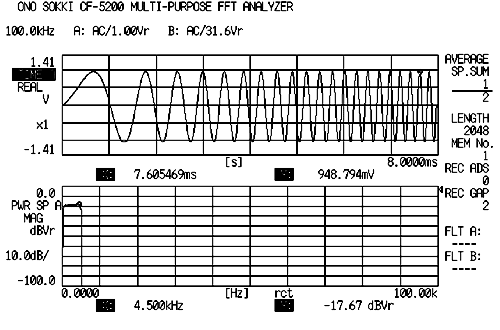
(2)マルチサイン信号
|
|
特 徴
-
正弦波を全ての分解能点に等しいレベルを持つ多重正弦波である。クレストファクターは約 3 である。信号の集中する度合いはほどほどである。
-
FFT の解析フレームと同期がとれ、窓関数にレキュタンギュラ窓が使用できるため、リケージエラーが発生しない。
-
常時同じ信号のため、加算の効果はないが、短時間に正確な周波数応答関数の測定が可能のため、近年では多く使用される。
-
周波数ズームで信号同期、帯域制限、分解能変更が行える機器では、ズーム分析により S/N の向上が期待できる。
-
正弦波を対数間隔に並べることにより、対数分解能が得られ、FFT 側で対数分解能周波数を選択して表示することにより、対数分解能測定が可能になる。
次の図は帯域制限したマルチサイン信号である。
|
|
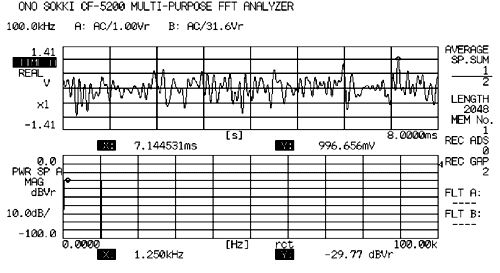
(3)合成インパルス
|
|
特 徴
-
正弦波の1波をピーク位置を合わせて合成した信号である。クレストファクターは約 30 である。
-
通常のインパルスと比較して、ズーム分析への対応が簡単である特徴を持つ。
-
当然の事ながら始めと終わりが“零”であり、FFT の解析フレームと同期がとれ、窓関数にレキュタンギュラ窓が使用できるため、リケージエラーが発生しない。
-
減衰率法での加振器への入力信号として使用できる。
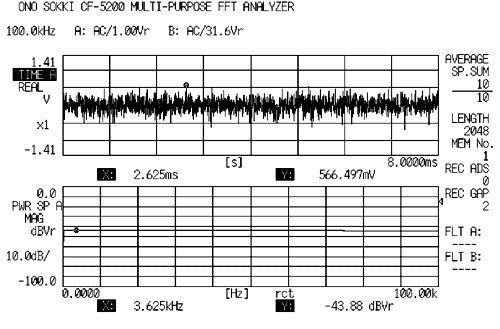
(4)ランダム信号
|
|
特 徴
-
通常 M 系列信号が使用され、クレストファクタは約 3 である。信号の集中する度合いは小さい。
-
あらゆる周波数の信号を持っているのでズーム分析でも使用可能である。
-
FFT の解析フレームと同期がとれないため、通常ハニング窓を使用するが、後述のように損失係数を測定する場合に限って、レキュタンギュラ窓が良い。ハニング窓を使用する場合はリケージエラーに注意すると共に、後述のようにハニング窓には損失係数の測定下限が有ることに注意して使用する必要がある。
-
これも帯域制限は可能なのでズーム分析の時は、ズーム帯域で帯域制限出きることが望ましい。
-
加算の効果が非常にあり、上図のように瞬時瞬時には欠落している周波数が多いので加算は充分する必要がある。
-
非線形要素を持った機器の測定には、バーストランダムを使用する。