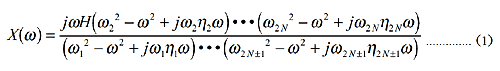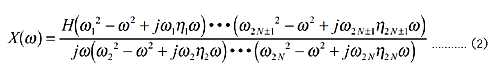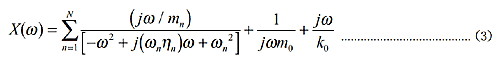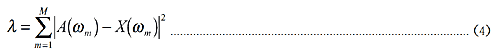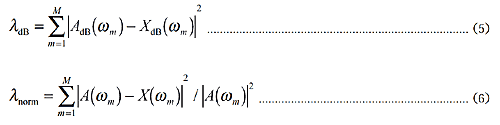16. FFT のズーム分析の必要性

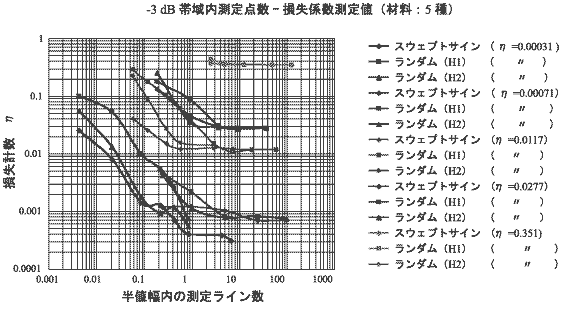
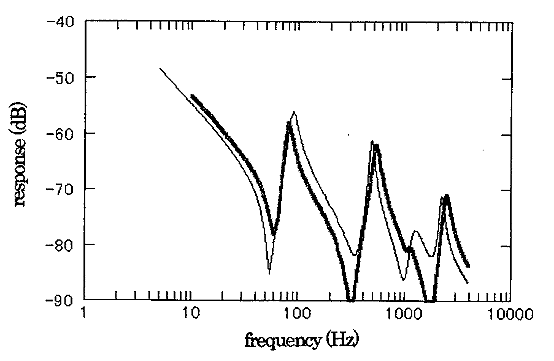
下図上は5種類の損失係数の異なる材料を、FFT アナライザでズーム分析を行い、周波数分解能を変えて測定したグラフである。横軸は半値幅法言う -3 dB 内（f₂ − f₁）にある FFT の測定点の点数である。このようにズーム倍率を上げていくと、段々測定される η は、ほぼ一定の値に収束する。この値を真値として誤差を計算して一緒に書き直したグラフが下の図である。

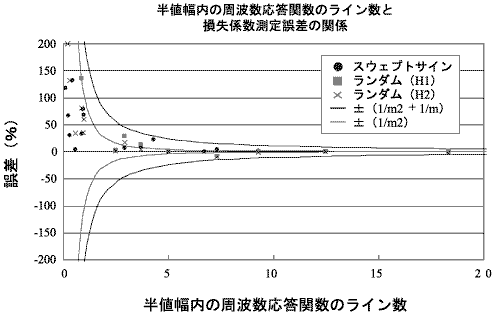
このグラフから言えることは半値幅内に存在する FFT の分解能点が、ほぼ 15 点あれば、損失係数の測定精度は 1％ 程度に収まるといえる。 このグラフから損失係数が小さい場合、ズーム分析は不可欠である。

17. ズーム解析とマスキャンセル

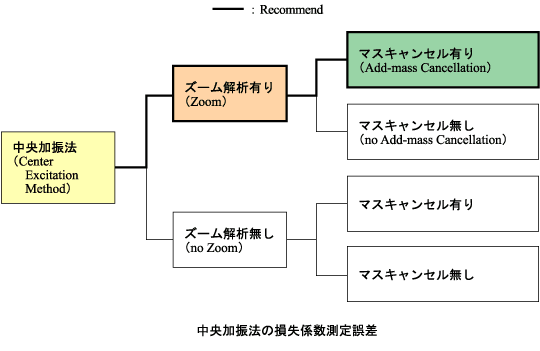
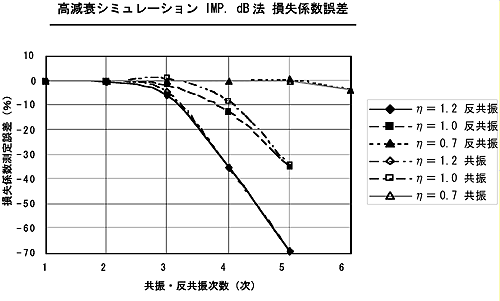
下図は、ズーム解析の有無およびマスキャンセルの有無による損失係数測定誤差の影響を示している。ズーム解析を行い、かつマスキャンセルを行った場合の損失係数測定誤差が最も小さくなる。特に、損失係数が 0.01 以下の場合は、ズーム解析の有無およびマスキャンセルの有無による損失係数の違いが顕著に現れるので注意する。

なお、損失係数に与える影響は、ズーム解析の有無の方がマスキャンセルの有無の場合よりも、かなり大きい。

18. 極零モデルを用いたカーブフィットによる損失係数の測定

（現状、損失係数測定において最も優秀なカーブフィット手法と考えるられるため、千葉工業 大学　鈴木英男教授の承認を得て、その論文を原文のまま掲載する）

１．はじめに

　最近の制振材料の製造技術の進歩に伴い損失係数の大きな材料の実用化が進んでいる。しかしながら、規格化された損失係数の測定方法としては ISO を含めても昔ながらの半値幅法しか存在ない。ここで、半値幅法とは、加振力に対する振幅、速度、加速度等の振動応答特性から求められる共振周波数 f₀ と、共振周波数におけるレベルが 3 dB 低下する周波数 f₁ と f₂ から η = （f₂- f₁）/ f₀ で求める方法である。ところが、最近では共振と反共振のレベル差が 3 dB もない材料も開発されており、このような材料に対して半値幅法は全く役に立たない。 さらに、最近の技術動向として、共振周波数における特性の鋭さとともに、反共振における特性の鋭さから損失係数を求める試みも行なわれている。たとえば、〔速度 / 力〕から求めた周波数応答関数の山（共振）の代わりに、谷（反共振）の特性から損失係数に対応する値を求めようとするものである。反共振の鋭さとその周波数での損失係数の値との関連は明確でないが、共振ならびに反共振の特性を含めてフィットすることは、山と谷のレベル差が少なくない材料の場合はどうしても必要なことである。
以上の目的から、共振および反共振の特性をフィットするために極零モデルを用いて〔速度 / 力〕または〔力 / 速度〕の特性にカーブフィットを行い損失係数を測定する方法が提案されている。ここでは、その概要を説明する。

2. 極零モデル

　極零モデルとは、加振点での応答特性を下記の式で表現する特性である。

　または；

ここで、η_n はそれぞれの共振および反共振での特性の鈍さを表すものである（共振の場合は損失係数）。ω_n は共振または反共振周波数、H は定数（正の実数）である。式（1）および式（2）はインピーダンス（〔力 / 速度〕）もモビリティ（〔速度 / 力〕）も表現することができるが、ここではモビリティを表すものとする。片持梁および両端自由梁のモビリティはそれぞれ周波数がゼロに近づくに従って増大および減少するので、片持梁のモビリティは式（2）に、両端自由梁のモビリティは式（1）に対応する。インピーダンス特性に対してフィットするときは逆数をとればよいので、それぞれ式を入れ替えて適用すればよい。極零モデルの最大の特長は、損失係数（反共振の場合も便宜上損失係数と呼ぶことにする）が陽な形で入っていることであり、山と谷の特性の鋭さを独立に定義できることである。参考のために、モード解析でよく用いられる数式モデルは以下のように表される。ここでは共振での損失係数のみが陽な形で入力できる。

3. カーブフィットに用いる誤差関数

　山と谷の特性を同等の誤差でフィットしようとすると、実測データとモデル特性の差の大きさを表現する誤差関数に工夫が必要である。従来からよく用いられる誤差関数λは；

である。ここで、A（ω m）は実測の特性、X（ω m）はモデルの特性である。共振では数字が大きいので同じ % の誤差でも大きく寄与し、反共振での特性の誤差は軽視される。この問題を解決するために、2 つの誤差関数が提案されている。

式（5）は周波数応答関数をデシベルで表現した特性をフィットに用いる方法である。式（6）は実測の特性で正規化することにより、山と谷での同じ誤差率が λ に同じ大きさで寄与するようにしたものである。これにより、これらの誤差関数を用いることにより共振と反共振の特性を同時にフィットすることが可能となる。

4. モデルデータへの適用

　式（1）または（2）から特性を計算し、それを実測データとみなしてフィットを行い、真値にどの程度近い値が得られるかを確認し、アルゴリズムの正しさを検証することができる。図 1 はその結果を示したものである。4 つの極と零を有する細い実線は、図-1 のタイプ B の極零モデルの共振、反共振周波数と対応する損失係数を与えて計算したもので、フィットの対象となる特性である。共振、反共振周波数は短冊形の中央加振の時の周波数分布となるような値を用いた。損失係数は 0.1、0.2 および 0.3 の値を適当に各共振、反共振に割り振った。太線は共振、反共振周波数にプラスまたはマイナス 10 ％の誤差をランダムに持たせ、損失係数は一律 に 0.15 の初期値を与えて計算したものである。
デシベル型の誤差関数を与えて計算したものである。デシベル型の誤差関数を用いてフィット行うと、フィット後に得られるパラメータの値は、8 桁以上の精度で正しい値が求められた（収束後の曲線は細線と重なっている）。カーブフィットによって損失係数を求めることの利点は、 測定するときの周波数分解能が半値幅法よりもはるかに粗くてもよいことである。図-1 のグラフでも、低域では折れ線グラフのように見えるほど粗くてもフィットが可能であることである。

5. 当カーブフィット手法での実測例

　

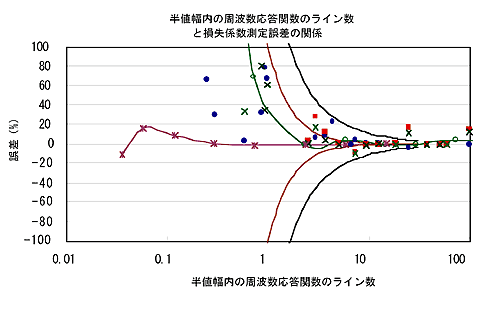
1. 小さな損失係数への対応

FFT のズーム分析の必要性のところで記載した半値幅内に必要な測定点数のグラフに重ね合わせると下図のようになり、当カーブフィット手法では半値幅内に 0.3 ポイント程度の測定点があれば、数％程度の誤差に収まる。

黒線：半値幅法の±（1/m2+1/m）のライン
赤線：半値幅法の±（1/m2）のライン
紫：当カー ブフィット手法で必要なライン数

2. 大きな損失係数への対応

シミュレーションで η＝ 0.7，1.0，1.2 という半値幅法では測定不可能な周波数応答関数を作成してこれを dB 法でカーブフィットした結果である。0.7 程度の損失係数では６次の共振次数まで、1.0、1.2 程度の損失係数では３次の共振次数まで、高精度で測定できることがわかる。

19. 二点吊り法

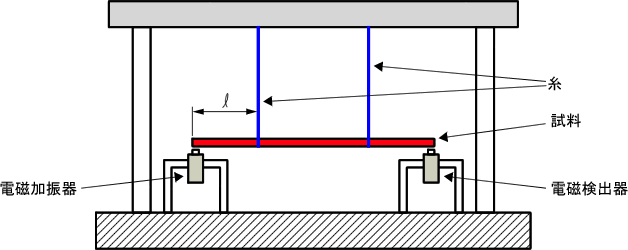
各振動モード毎の節を吊る方法である。動かない位置を吊ることから、従来から最も小さな損失係数から測定できるとされることから金属単品の損失係数測定に多用される。当方法での欠点としては各モード毎に、吊る位置を変えなければならないとされる点である。加振は非接触の電磁加振器を使用し、応答は同じ加振器を電磁速度センサーとして使用するのが一般的である。（電磁加振器／検出器については片持ち梁法で使用する機器を参照のこと）

の位置について

※試験片の長さを100％とした場合の左右端からの位置を％で表したものである。多数ある場合はどこを吊っても良い。

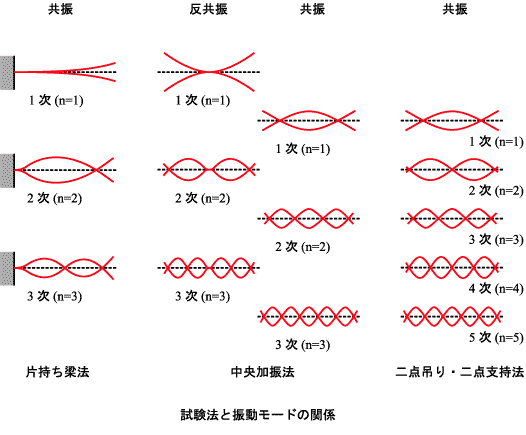
20. 損失係数の振動モード依存性

下図の試験法と振動モードの関係をみると、片持ち梁法の試験片の長さが中央加振法の試験片の長さの 1/2 の場合、片持ち梁法の共振と中央加振法反共振の振動モードは同じであることが判る。また、二点吊り法、二点支持法の共振と中央加振法共振の振動モードは同じであることが判る。

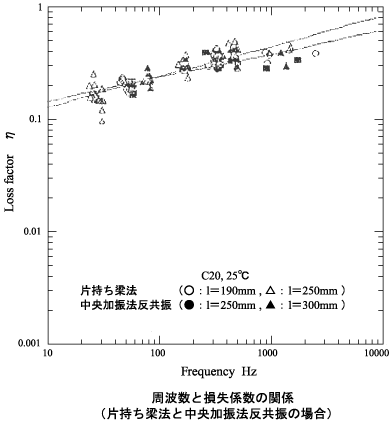
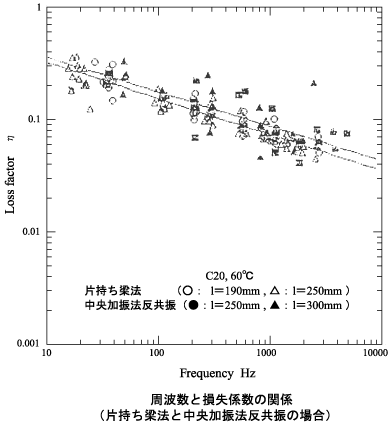
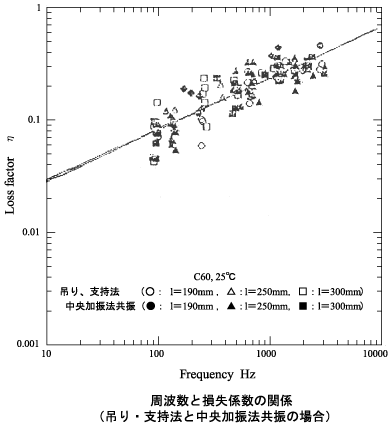
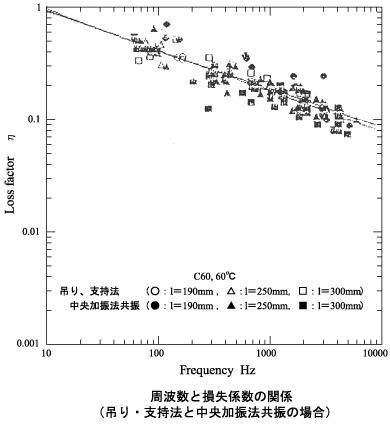
次の４つの図は、1. 片持ち梁法の共振と中央加振法反共振、2. 二点吊り法、二点支持法の共振と中央加振法共振での両者の損失係数を比較したものである。これらより、以下のことがいえる。

[前のページに戻る]

［次ページへ続く］