13. 片持ち梁法と中央加振法の選択
片持ち梁法と中央加振法では使用上で下記の特徴を持つので、注意が必要である。
| 片持ち梁 | 中央加振 | |
| 温度試験の簡便さ | ○ | △ |
| 特に高温の時の対応 | × | バイブロチャンバーで可能 |
| クランプ部の問題 | 有り | 無し |
| 1次モードの測定 | 不可 | 可 |
| 高次モードの測定 | 難しい | 簡単 |
| マスキャンセル | 不要 | 要 |
| 柔らかい材料単品の測定 | 可 | 不可 |
| 反共振側の測定 | 難しい | 容易 |
| 価 格 | ○ | × |
14. 各試験法より求めた損失係数の比較
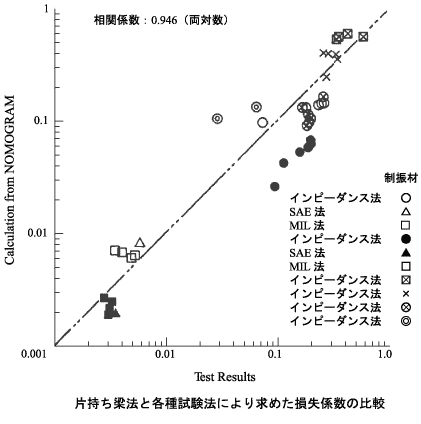
片持ち梁法より求めた試験片のデータを使用して、制振材料の損失係数とヤング率を換算周波数ノモグラムの形で求め、この換算周波数ノモグラムを使用して、インピーダンス法、SAE 法、MIL 法の試験片の損失係数を推定した。 下図は、このようにして推定した損失係数を縦軸にとり、インピーダンス法、SAE 法、MIL 法で求めた損失係数実験値を横軸にとって、両者の関係をプロットしたものである。 図より、両者の相関係数は 0.946 であり、片持ち梁法で求めた損失係数とインピーダンス法、 SAE 法、MIL 法で求めた損失係数は、かなり良く一致していることがわかる。
|
|
15. マスキャンセル
中央加振法で試験を行う場合、一般的にはインピーダンスヘッドを使用して駆動点インピーダンスやモビリティ等を測定して損失係数を測定する。この場合、インピーダンスヘッド自体が加速度を測定するためのマス(質量)を持っており、これが力ゼロの場合でも、実際はこのマス分だけ力センサーで計測されることになる。したがって、試験片の重さプラスこの質量分が測定されるため、インピーダンスが正しく計測されないことになる。このため試験をする場合には、あらかじめこの付加質量分を補正する必要がある。この操作を一般的には、マスキャンセルと呼んでいる。
|
|
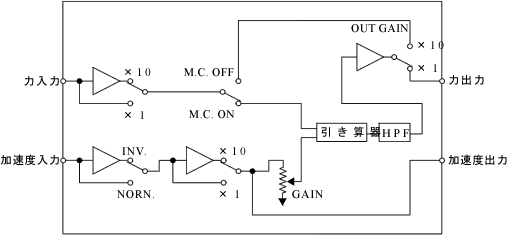
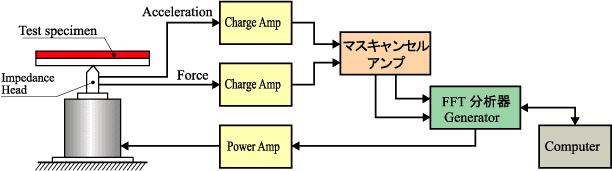
上図は、マスキャンセルの方法の一例を示しており、下図は実際にマスキャンセルを行うための試験システムの一例を示している。
|
|
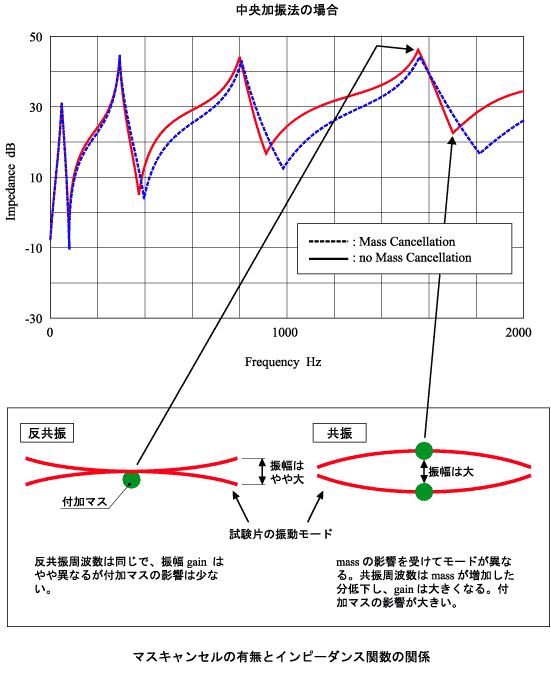
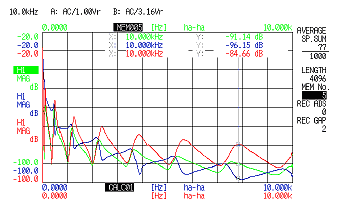
下図は、このシステムを使用して測定したインピーダンスの一例を示す。マスキャンセルの有無により、特に共振周波数側が異なってくることがわかる。
|
|
■マスキャンセルを FFT の計算で行う場合の計算式
赤:緑:マスキャンセルなしのモビリティー
青:計算1[(V / F)−(V / F0)]によって求めたマスキャンセル後のモビリティー
赤:マスキャンセルアンプを用いたマスキャンセル後のモビリティー
|
|
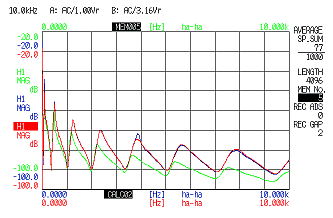
赤:緑:マスキャンセルなしのモビリティー
青:計算2[(V / F)(1 / H)−(V / F0)(1 / H)](1 /
H)によって求めたマスキャンセル後のモビリティー
赤:マスキャンセルアンプを用いたマスキャンセル後のモビリティー
|
|
機械インピーダンスの波形は省略するが FFT 等の計算でマスキャンセルを行う場合
-
分子が F の関数(機械インピーダンス等)は(F / V)−(F0 / V)の様にそのまま引き算して良い。
-
分母が F の関数(モビリティー等)を使用する場合は、一旦周波数応答関数の逆計算 (1 / H)で F を分子に持ってきて、付加マス分も逆数計算をして引き算をし、さらに逆数計算をして元の分母が F の関数に戻す必要がある。 実際の計算式はワークなしの周波数応答関数を FRF1、ワークを載せたマスキャンセルなしの周波数応答関数を FRF2、マスキャンセル後の周波数応答関数を FRF3 とすると;
FRF3 = 1/((1/FRF2)−(1/FRF1))
である。
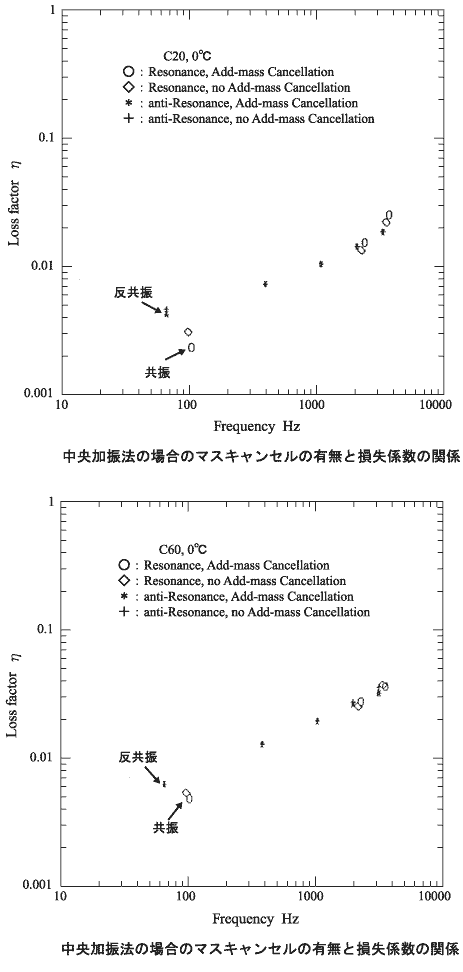
また、中央加振法の場合のマスキャンセルの有無と損失係数の関係を示す。下図より、損失係数が 0.01 より小さい場合は、マスキャンセルの有無により損失係数がやや異なることがわかる。
|
|