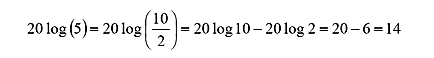1. はじめに
電気、通信、光学、音響、振動などいろいろな分野でデシベル(dB)が使われています。ここでは、デシベル(dB)の基本的な定義、それを使う意義、その便利さ、いろいろな分野での使われ方など、をまとめています。
2. 対数について
デシベル(dB)の定義には対数が使われており、対数の性質を理解することがすなわちデシベルを理解することですから、とりあえず対数の説明から始めます。
【注意】
本章は文系向けの内容なので、理系の人はスキップしてください。
2-1 指数とは
大きな数字を表すときは、数字桁数が増えるので、べき乗表現をよく使います。例えば、100万という数字は;
100万 = 1,000,000 = 10 6
と10 のべき乗で表現すると、桁も少なく簡便になります。一般に、ある数 N を任意の正数 a のべき乗で表したとき;
|
|
を N の指数表現と呼び、aを底、m を指数と呼びます。これをより一般化して m を整数だけでなく実数まで拡張したものが指数関数となります。
指数に関する重要な公式;
|
|
|
|
ここで、m を対数(logarithm)、a を底(base)、N を真数(anti-logarithm)と呼びます。注意することは、同じ m であっても、(2-1)式と(2-4)式で式の表現方法の違いにより、呼び名が違うことです。N を中心に表記したのが指数関数、m を中心に表記したのが対数関数で、お互い逆関数となります。英語文法で言えば、いわば能動態と受動態のような関係に当たります。
(2-4)式の m を(2-1)式に代入すると;
|
|
の関係式が得られます。さらに、指数公式と同様に、対数に関する重要な公式が得られます。
|
|
対数は、16世紀にジョン・ネイピアらが、乗算やべき乗計算を簡単にするために発見したと言われています。電卓やコンピュータのない時代においては大変重宝する計算方法であったようです。
2-3 底の違いによるいろいろな対数
(2-4)式における底aは具体的にはどのような値が良いのでしょうか?
底の違いにより、以下の対数が使われています。
|
表1 底の違いによるいろいろな対数 |
| 底a | 対数の種類 | 応用分野 |
|---|---|---|
| 10 | 常用対数 | 一般技術計算、デシベル計算 |
| e(ネイピア数) | 自然対数 | 解析学などの数学 |
| 2 | 二進対数 | 情報理論 |
今回の主目的のデシベル(dB)には、常用対数が使われますので、以後対数といえば常用対数を指すこととします。
また、(2-4)式における底 a =10 は省略して表記します。
|
[例] 100万の対数は6 ⇒ log (1,000,000) = log (10 6 ) = 6 |
2-4 具体的な対数の値
右下の表3は、1から10までの真数に対する対数値で、現在では電卓で簡単に求めることができますが、次表2のように、いくつかは他の値から計算可能です。
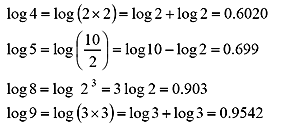
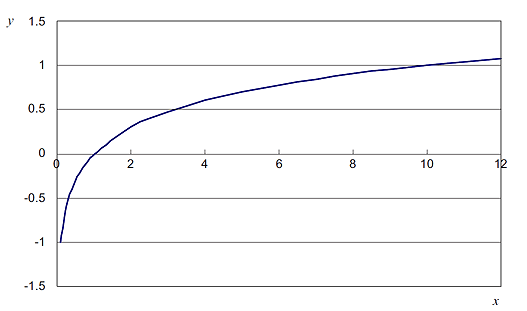
図1は常用対数 ![]() のグラフ例で、真数xが整数の時の数値例が表3となっています。 真数x
の値により;
のグラフ例で、真数xが整数の時の数値例が表3となっています。 真数x
の値により;
x < 1 の時 y < 0
x = 1 の時 y = 0
x > 1 の時 y > 0
となります。このことは、これから説明するデシベル値は負の値も取り得ることを意味しています。
|
|
表3 対数の数値例
|
3. デシベルとは
3-1 デシベルの定義
デシベルは、電気系において電力伝送減衰の度合い(すなわち比率)を表すのに最初に用いられました。 いま、2点の電力をP1 と P2 としてその比の常用対数をとりそれを x とすると;


この x を、ベル(B)と呼びます。これは、アメリカのアレクサンダー・グラハム・ベル(Alexander Graham Bell)が最初に電話における電力の伝送減衰の表現に用いたことに因んでいます。 また、ベル(B)そのものでは値が大きすぎるため、その 10 分の1 であるデシベル(deci Bel = dB)が通常使用されています。
【注意】
「ベル(B)そのものでは値が大きすぎる」という意味は、1ベルという量的値が大きいという意味であって、数値的には小さくなります。例えば、7Bは 70 dB と同じ量となります。これは、1 m の長さと 1 mm の長さとを比べてみれば明らかでしょう。
デシベル Lは、2点間(P1、P2)の電力比の対数の10倍として定義されます。

このように、デシベルの定義はそもそも電力比ですが、電圧比(あるいは電流比)でもよく使われています
電力は、電圧(あるいは電流)の 2乗に比例することから;
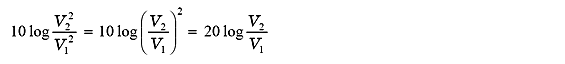
となりますので、電圧比でのデシベル[L]は、2点間(V1、V2)の電圧比の対数の20倍と定義されます。

このように電力(パワー)と電圧(実効値、またはリニア値)のどちらの比であっても同じデシベル値となります。
【注意】
-
電気や音(振動)などの物理信号は通常交流信号なので、その物理量は実効値が使われています。本資料においては、デシベル計算に使われる物理量はその実効値です。
- 伝送回路理論計算では自然対数を使ったネーパ(Np)を使うことがあります。自然対数を ln で表記すると;
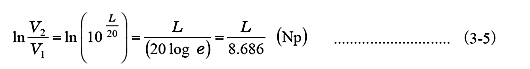
と変換できるので、1Npは 8.686 dB に相当します。ネーパは、先の 2章の対数を発明したネイピアからとっています。
3-2 具体的なデシベルの値
表4は、良く使うデシベル値とそれに対する真数値(電力比と電圧比)の関係を表しています。この表を使って、電圧の倍率に対するデシベル値(概略値)を簡単に求めることができます
| dB値 | -20 | -6.02 | 0 | 3.01 | 6.02 | 10 | 20 | 30 | 40 |
|---|---|---|---|---|---|---|---|---|---|
| 電力比 | 0.01 | 0.25 | 1 | 2 | 4 | 10 | 100 | 1,000 | 10,000 |
| 電圧比 | 0.1 | 0.5 | 1 | 1.41 | 2 | 3.16 | 10 | 31.6 | 100 |
|
[例]
5倍は?
|
【注意】
上表4にあるように、真数値が 1 より大きい時 dB値は正値、真数値が 1より小さい時 dB 値は負値となります。これは前述した対数の性質そのものです。すなわち、デシベル値が負の値となっても真数値自体が負の数となるわけでなく、電力比(または電圧比)が 1より小さくなっているだけにすぎません。
3-3 絶対値を表すデシベル
デシベルは、定義にもあるよう 2つの量の比を表すもので、あくまで相対レベル値を意味しています。基準となる値(比の分母)を一定の物理量として定義しておけば、その場合のデシベル値は、物理量の絶対値として簡単に換算することできるので、絶対レベル値と見なすことができます。
一般に、電気や音(振動)などの分野で物理量の大きさをデシベルで表現した量を「レベル(単位dB)」と呼びます。これ以降では、レベルとデシベルは、ほぼ同義として説明しています。
ここで、電圧値を表現する例を考えます。電圧比の基準値を 1 Vと定義しておくと、任意の電圧値をデシベル値で代用して表現できます。この時の単位は、dBV となります。例えば、x(V)をy(dBV)とすると;

と、計算時には基準値 1 を省略することができます。
【注意】
今後、絶対基準値が 1であれば、絶対レベル値の定義式は 1を省略表記します。 すなわち先の表 4の電圧比の値を電圧値と見なして表を利用できます。
|
[例]
2 V ⇒
6 dBV |
表5 電圧レンジとデシベル
|
電圧値でなく他の物理量でも、全く同様です。例えば、振動加速度の例で考えます。基準値を1 m/s2で定義すれば、5 m/s2 は、約 14 dBm/s2 の意味となります。
これまでの例では、基準値は 1
で簡便な計算でしたが、例えば音響分野で良く使われる音圧レベルにて定義される基準値は1ではありません。しかし、この場合でも、同様にしてそのデシベル値は絶対値(音圧値)を表現しています。
これについては、後述します。デシベル自体は、SI
単位系ではありませんが、音響分野では単位に準じた量として使われています。
まとめますと、絶対レベル値は、dB を単位のように見なして物理量そのものを表していることになります。ですから、単にdBでなく、“dB ○○”というような表記をしている場合も多くあります。
3-4 デシベルを使うメリット
これまでの説明にもあるように、デシベルを使うメリットはたくさんあります。以下、代表的な理由を述べます。
-
アンプのゲインなど大きな数字を表すのにデシベルを使うと、少ない桁数で表現できる。
例えば、50,000倍は 94 dB。 -
多段のアンプや複数の伝達系などの特性評価する場合において、乗算や除算が加算や減算に置き換えることができ、簡単に計算できる。
-
“人間の感覚量は刺激量の対数に比例する”というウェーバ・フェヒナーの法則があり、感覚値(特に音響)の評価に適している。
3-5 デシベル(dB)とパーセント(%)
デシベルも百分率(パーセント、% )も比率を表していますから、数値の相互変換は可能です。この場合でのデシベルは通常電圧比と見なします。例えば、10 %は、20 log (10/100) = −20 より、−20 dBとなります。
抵抗値許容誤差や、センサーの周波数特性範囲の許容差を表すとき、±5 %と言うような基準値からの比で表現する場合があります。この数値もデシベル値に変換できます。例えば+10 %ということは、(1+10/100)倍となりますので、20 log (1.1) = 0.83、すなわち 0.83 dB に相当します。同じように −10 %は、20 log (0.9) = −0.92、すなわち−0.92 dB に相当します。
ここで、注意することは、% はリニアで、dBは対数であると言うことです。
+1 dB ⇒
+12.2 %
−1 dB ⇒
−10.9 %
となり、等比的(対数的)に等間隔であることは、リニア間隔は+側が広くなります。非常に大ざっぱな言い方をしますと、±1 dBは ±10 %程度となります。