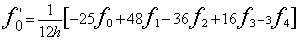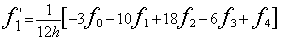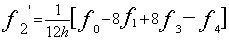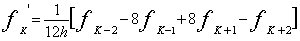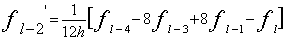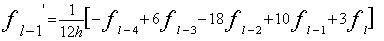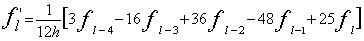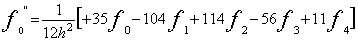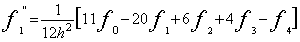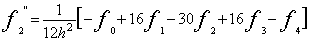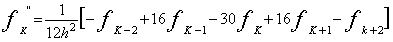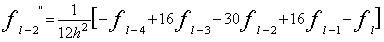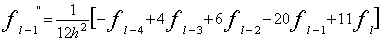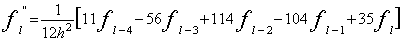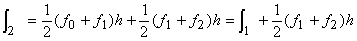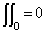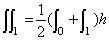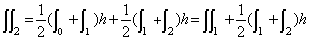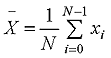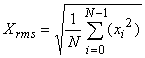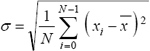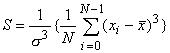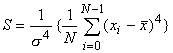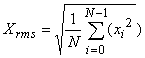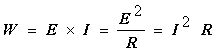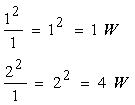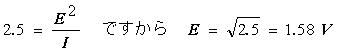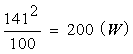サイン波では、実効値はピーク値の１／√2になります。パワースペクトルの各ラインのデータはその帯域の信号の実効値
の２乗、すなわち２乗平均値になります。
実効値とは
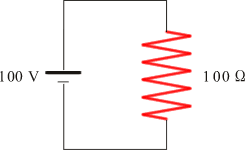
例として、電熱器を考えてみます。電熱器に直流電圧をかけると熱が発生します。電熱器のニクロム線（最近はセラミックヒーターかも知れませんが）は抵抗ですから回路としては、下図1のように表されます。
図1
電圧が100 V、抵抗値が100Ωの場合に発生するエネルギー（熱）を考えてみると、抵抗に流れる電流はオームの法則；
から、I = E/R = 100 / 100 = 1 (A)となり、また、電力 W は、W
= E × I = 100 × 1 = 100 (W) になります。いちいち電流を計算するのは面倒なので、一般的には、I
= E/R より；
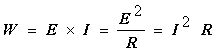
が良く用いられます。100 Ω の電熱器に 100 V をかけると 100 W 分の熱が発生することが分かりました。ところで、家庭用の電源は、実効値
100 V ですが、直流ではなく、関東では 50 Hz の交流（正弦波）です。この家庭用電源に 100 Ω の電熱器を接続すると何
W 分の熱が発生するのでしょうか？
答えは、100 W です。つまり、”実効値とは同じ仕事をする直流電圧に置き換えたもの”なのです。では、同じ電熱器を
AC 200 V で使用したらば何 W を発生させるでしょう？＜実際にはこんなことをしたら電熱器が壊れてしまうでしょうが＞
AC 200 V は、DC 200 V と同じパワーを持っているので、DC 200 V として考えると、2002／100
= 400 W となり、200 W にはなりません。これは、”電圧が
2 倍になると電流も 2 倍になり、電力は 22 の 4 倍になる”ためです。では、次の図
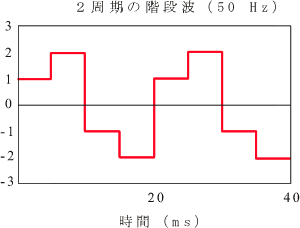
2 の実効値はどうなるでしょう？
図2
単純に絶対値を平均すれば 1.5 V ですが、実際に発生する電力を考えてみましょう。抵抗値が
100 Ω では計算が面倒なので 1 Ω で考えます。1 V の時と 2 V の時に発生する電力は以下の式になりますが、抵抗
1 Ω を省略しても結果は変わりません。
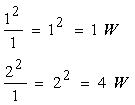
電圧の 2 乗したものは、1 Ω の抵抗に発生するパワー（電力）になります。電圧、電流を 2
乗したものを見たらパワーだなと思ってください。（1 Ω の場合、電圧と電流は等しくなるので、式 2 から電流の 2 乗もパワーになります）
平均電力は、1 W の区間が 1/2 と 4 W の区間が 1/2 ですから 2.5 W になります。つまり、この波形は、1
Ω の抵抗に 2.5 W の電力を発生させる DC 電圧と同じパワーを持っていることになります。
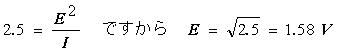
となり、実効値は 1.58 V であることがわかります。
実効値はパワーの平均をルートしたもの。言い換えると、実効値はルートした 2 乗の平均のことで、これを英語では
「root mean square」といい、特に実効値であることを強調したい場合には、単語の頭文字をとって「rms」と表記します。
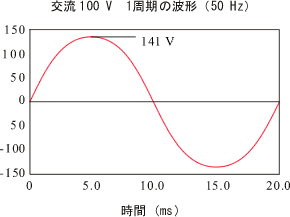
正弦波の実効値はピーク値の 1/√2 = 0.707、ですから家庭用の 100 V 電源の波形は、下図
3 のようにピーク値が実効値の √2 倍の 141 V になっています。（ちなみに、平均値は 2/π = 0.637 です）
図3
再び、この電源に 100 Ω の電熱器を繋げてみましょう。そうすると、最大電力は；
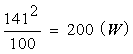
から、200 W になります。最小電力は 0 W であることは明らかですので、発生する電力は
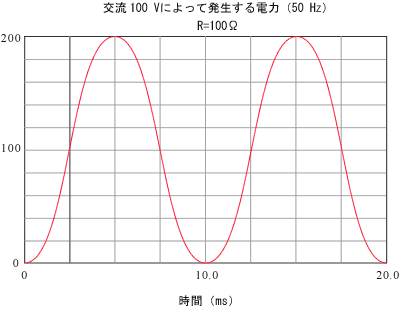
0 W と 200 W の間を往ったり来たりすることは容易に想像できます。この様子を図示したのが、下図 4 です。この時の平均値は、100
W であることは明らかでしょう。
図4
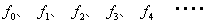はサンプルデータとする。
