3. 減衰の効果
ここまでは、振幅が指数関数的に減衰していく状態を前提に減衰比や損失係数の求め方について説明しましたが、ここからは減衰比が実際の振動で物理的にどのような意味を持つかについて簡単に解説します。損失係数や Q 値については減衰比から容易に換算できますので、ここでは減衰比に絞って話を進めます。
3-1 自由振動における減衰の効果
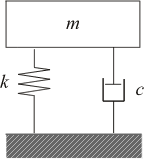
自由振動とは「外力が加わらない状態」での振動です。そのままではいつまでも静止したままですが、初期条件として初期変位や初期速度を与えると振動を始めます。例として図4 に示すバネマスモデルを考えると、最初に質量 m を引っ張ってバネ k にある変位(初期変位)を与えておいて急に離すと振動を始めますが、これが自由振動です。
|
図4 自由振動モデル |
減衰力 c がない場合には自由振動は永久に続き、このときの振動周波数 ω0 は次式で表されます。
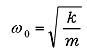 |
(11) |
ω0 を固有振動数といいます。経験的に知られているように、実際にはこの自由振動は永久には持続せず、減衰力 c が働いて図1 に例示したように振幅は徐々に小さくなり、やがて静止状態になります。 このとき、c の値が次式の ccより大きいか小さいかによって挙動が異なります。
|
|
(12) |
ccを限界減衰率と言い、ccと c の比が本稿の主題である ζ(減衰比)です。
|
|
(13) |
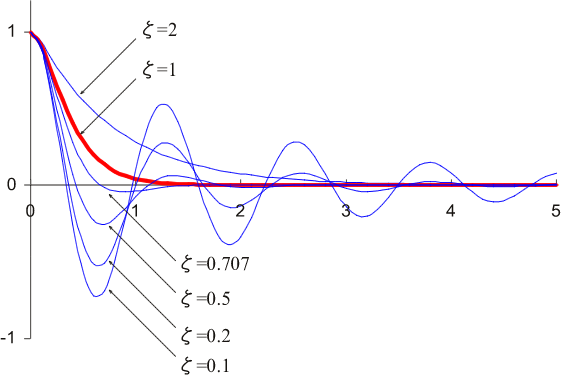
上述のように自由振動の振幅は ζ の値によって大きく変化します。図5 にその例を示します。
|
図5 自由振動の応答 |
ζ < 1 の場合の減衰自由振動の振幅は次式で表されます。
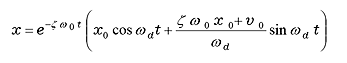 |
(14) |
ここで、
x0:初期変位
v0:初期速度
また、ωd は減衰系の固有振動数と呼ばれ、次式で表されます。
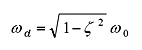 |
(15) |
ωd は ω0 に比べていくらか小さくなりますが、現実の振動系では ζ の値は小さいので ωd は ω0 に近い値となります。 式(14)でわかるように、減衰振動系の挙動は初期条件と減衰比 ζ で決まります。図5 は初期速度0で初期変位を1とした場合の減衰比 ζ の違いによる応答の様子を示したものですが、減衰比 ζ によって挙動が大きく異なることがわかります。
なお、ζ ≧ 1 の場合には式(14)では計算できず、別の式によります。ここではその計算式は省略しますが、比較のために図5 には応答を示しています。ちなみに ζ = 1 の状態を臨界減衰と言い、ζ > 1 を過減衰、1 > ζ > 0 を減衰不足と言います。過減衰および臨界減衰では振動することなく減衰運動となります。図5 では解りやすいように ζ = 1(臨界減衰)を強調していますが、これは振動するか否かの境界を示すだけのことであり、ことさら臨界減衰が重要という意味ではありません。
また ζ
= 0.707(=
![]() )の場合の応答も示してありますが、これは次の定常振動において重要な値です。また、多少オーバーシュート(アンダーシュート)はあるものの、整定時間(応答が目標値の5%以内に収束する時間)が最短となる場合の値として制御系など応答時間を重視する場合によく使われる値でもあります。
)の場合の応答も示してありますが、これは次の定常振動において重要な値です。また、多少オーバーシュート(アンダーシュート)はあるものの、整定時間(応答が目標値の5%以内に収束する時間)が最短となる場合の値として制御系など応答時間を重視する場合によく使われる値でもあります。
3-2 定常振動における減衰の効果
次に、自由振動系に外部から継続した力が加えられた場合を考えます。
外力が作用する場合の振動を強制振動と言いますが、外力が正弦波であって、外力が加えられてから十分な時間が経過した状態(定常状態)における振動を定常振動といいます。これに対し、外力が加えられてから定常状態に至るまでの経過を過渡状態と言いますが、これについては次項で説明します。
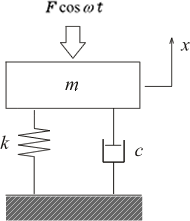
図6 に示すように1自由度振動系に![]() という加振力が加えられたモデルを考えます。
という加振力が加えられたモデルを考えます。
まず記号と式を再確認しておきます。
 |
図6 強制加振振動モデル |
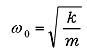 |
(11) |
|
|
(12) |
|
|
(13) |
加振力は周波数 ω の繰り返し力ですから、それによって駆動される定常振動も同じ周波数の振動になります。ただし振幅と位相は異なるものとなり、ここではその振幅と位相を求めます。
図6 の系の運動方程式は次式で表され、この方程式を解くことで、定常振動の振幅と位相を求めることができます。
|
|
(16) |
定常振動の式を;
|
|
(17) |
とすると、振幅 xa と位相 φ は次式で表されます。
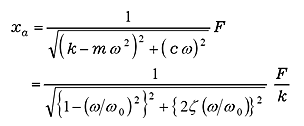 |
(18) |
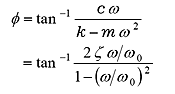 |
(19) |
式(18)において、F / k は静的力 F を加えたときの静的変位量ですので、これを xs とすると、式(18)は;
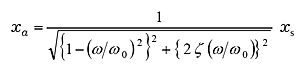 |
(20) |
と表すことができます。つまり、定常振動の振幅は静的変位量 xs と固有周波数 ω0 および減衰比 ζ の周波数応答関数として表されることを示しています。
さらに式(20)を変形した;
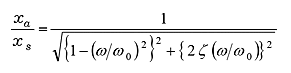 |
(21) |
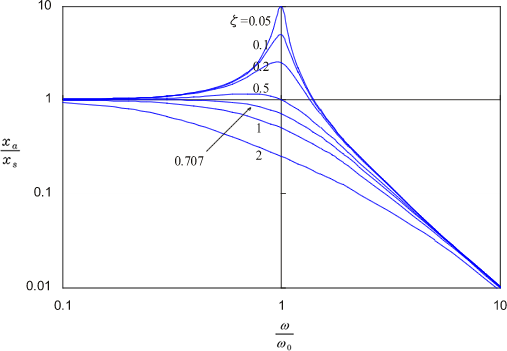
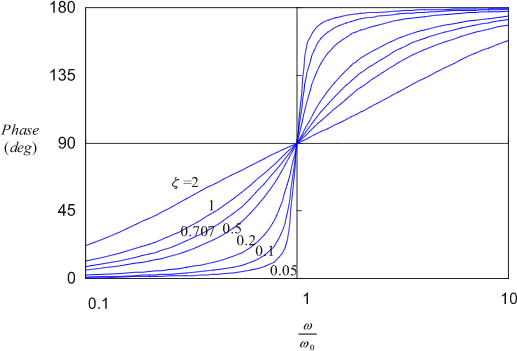
は振幅倍率と呼ばれます。横軸にω / ω0、縦軸に振幅倍率をとり、対数で図示したのが図7 です。これは、定常振動は ω0付近で共振することを示しており、また振幅倍率は減衰比 ζ によって大きく変化することがわかります。
|
図7 振幅倍率 |
振幅倍率の特徴をまとめると:
-
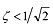 のとき、
のとき、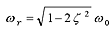 を共振周波数とする共振点を1つ持つ。共振周波数
ωr は
ζ が大きいほど低くなるが、低減衰系すなわち
ζ が小さいとき(概ね
ζ < 0.05)には
を共振周波数とする共振点を1つ持つ。共振周波数
ωr は
ζ が大きいほど低くなるが、低減衰系すなわち
ζ が小さいとき(概ね
ζ < 0.05)には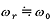 、つまり固有振動数で共振する。
、つまり固有振動数で共振する。 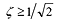 では共振しない。
では共振しない。
振幅倍率は共振周波数で最大となる。
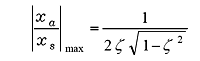 |
(22) |
ζ が小さい場合には;
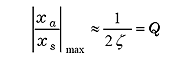 |
(23) |
-
となり、Q 値に等しくなる。ζ が小さい場合、すなわち共振が鋭い場合には Q 値で扱われることが多い。
-
共振点より低い周波数では振幅倍率は 1 に漸近する。
-
共振点より高い周波数では振幅倍率は
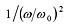 、すなわち
−40 dB/decade の傾斜に漸近する。
、すなわち
−40 dB/decade の傾斜に漸近する。
式(19)は加振力と定常振動の位相差を表しています。これをグラフ化すると図8になります。
|
図8 定常振動の位相遅れ |
これからわかることは;
-
加振力の周波数が ω0 より低い周波数領域では定常振動の位相遅れは 0 deg に漸近、つまり加振力から少し遅れた位相で振動する。
-
ω0 より高い周波数領域では 180 deg に漸近、つまり加振力と逆位相に近い位相で振動する。
-
ω = ω0 では 90 deg、すなわち 1/4 周期遅れて振動する。
-
ζ が小さいと ω0 付近で位相は急変し、ζ が大きくなるにつれて変化はなだらかになる。
3-3 過渡振動における減衰の効果
前項の定常振動では外力が加えられてから十分な時間が経過した状態を考えましたが、次は外力が加えられた時から定常状態に至るまでの状態、つまり過渡状態について考えてみます。
図6 の振動系で考えると、その運動方程式は式(24)となりますが、ここではわかりやすいように外力を![]() として、初期条件は完全静止、つまり初期変位と初期速度はゼロとして考えます。
として、初期条件は完全静止、つまり初期変位と初期速度はゼロとして考えます。
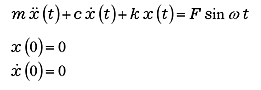 |
(24) |
この系は線形ですので重ね合わせの理が成り立ち、解はこれまで見てきた外力による振動成分と自由振動成分の和の形で得られます。
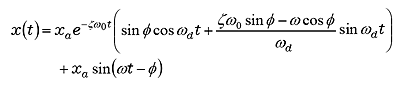 |
(25) |
ここで;
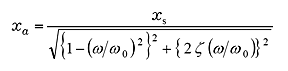 |
(26) |
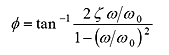 |
(27) |
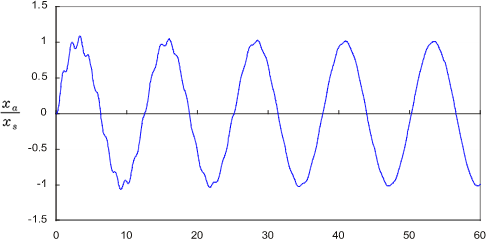
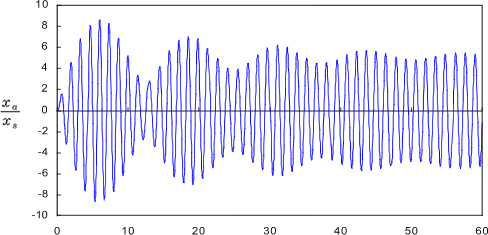
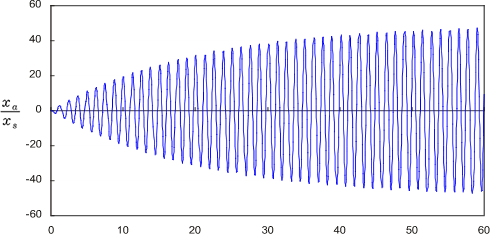
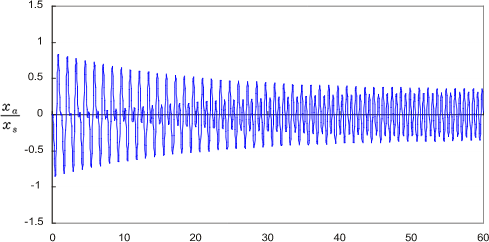
式(25)の第1項は自由振動成分で、時間の経過とともに減衰し、ついには第2項の定常振動成分だけになります。この様子をグラフに表したのが図9 の 1 から 4 です。ここでは ζ = 0.01として、ω/ω0 を 0.1、0.9、1.0、2.0 と変えた時の過渡応答の変化を示しています。
-
ω/ω0 が小さい時には定常振動に自由振動が重畳しているだけで、自由振動は時間の経過とともに減衰して定常振動に移行する。
-
ω/ω0 が 1 に近づく、すなわち加振周波数が固有振動周波数に近づくと振幅が増大するとともに、唸りを生じることがわかる。
-
ω/ω0 = 1 すなわち加振周波数が固有振動周波数に一致すると、振幅は時間にほぼ比例して増大し、非常に大きな振幅に至る、すなわち共振状態となる。
-
ω/ω0 > 1 では振幅は小さくなってくるが、複雑な波形を呈する。
ここでは過渡状態を解りやすく示すために ζ = 0.01 と小さな値としましたが、ζ が大きいと自由振動は早く収束するとともに、定常振動の振幅も小さくなります。その振幅は図7に示すとおりです。逆に ζ が小さいと過渡状態はなかなか収まらず、不安定な状態が長く続くことになります。また定常振動の振幅も大きくなり、特に ω/ω0 = 1 付近の周波数では、始めは小さな振動であっても時間とともに徐々に振幅が増大して非常に大きな振動に成長することになります。(図9-1 〜 4 は縦軸のスケールが異なることに注意)
| 図9-1
ζ =
0.01 |
|
| 図9-2
ζ =
0.01
|
|
| 図9-3
ζ =
0.01
|
|
| 図9-4
ζ =
0.01
|
|