1. はじめに
機械が稼働していれば振動は避けられない現象ですが、振動は不快なだけでなく故障の原因ともなり、甚だしい場合には機械の破壊に至ることもあります。振動が起きてから対策を施していたのでは手間と費用がかかるため、機械を設計する際には振動について予め十分な検討を行い、振動を起こさないあるいは減らすための対策を施すこと重要となってきます。またビルや橋梁などの建造物においては振動対策が必須です。
機械や構造物の振動対策としては、大きく次の4種類の方法が考えられます。
-
振動のモトを絶つ。
-
振動し難い構造とする。
-
減衰を与える。
-
振動を打ち消す。
本稿では、このうちの「減衰」に着目し、減衰の特性をあらわす係数である減衰比や減衰率、Q 値といった係数についてその求め方と、振動という現象においてその係数が持つ効果について解説します。
2. 減衰特性をあらわす係数
減衰振動や制振材料などの減衰特性を表す係数には、減衰比(ダンピングファクタ)、対数減衰率、損失係数、Q 値などがあります。それぞれの係数の定義や物理的な意味は後から説明することにして、ここではまず、これらの係数の求め方を説明します。
2-1 対数減衰率 δ
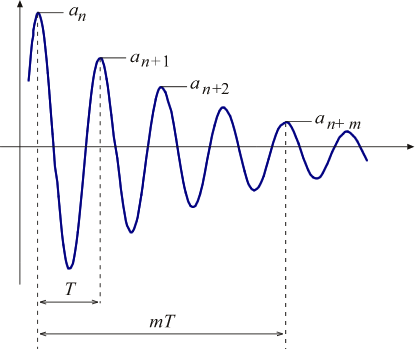
一般に減衰自由振動波形の振幅は図1のように指数関数的に減衰します。そこで隣り合う振幅の比の対数をとってみると常に一定の値となります。この隣り合う振幅の比の自然対数を対数減衰率と言い、減衰特性をあらわす解りやすい係数として広く使われています。物理上の特性値である減衰比や損失係数は対数減衰率から計算できます。
|
図1 対数減衰率 |
時刻 tn における n 番目の振幅を an 、同様に n + 1 、・・、n + m 番目の振幅を an + 1 、・・・、an + m とすると、対数減衰率 δ は次式で定義されます。
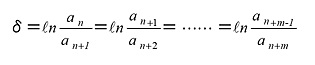 |
(1) |
1周期だけでは精度が不十分な場合には、m 周期とって計算します。
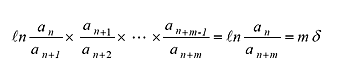 |
(2) |
よって、
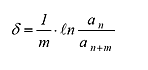 |
(3) |
δ より減衰比(ダンピングファクタ)ζ および損失係数 η を求めることができます。
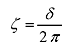 |
(4) |
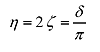 |
(5) |
2-2 ヒルベルト変換による対数減衰率と減衰比の算出
FFT アナライザーのヒルベルト変換機能を使うと対数減衰率 δ と減衰比 ζ を求めることができます。
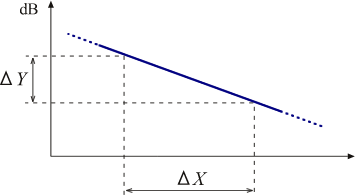
図1の減衰波形を時間軸波形としてFFTアナライザーに取り込み、ヒルベルト変換を行って振幅の包絡線に変換し、Y 軸をdB 表示にすると図2のような右下がりの直線が得られます。
|
図2 ヒルベルト変換による算出 |
Δ カーソルを使って、この直線部分の2点間の ΔX と ΔY を求めると、次式により対数減衰率 δ と減衰比 ζ が計算できます。
振動周波数を fd とすると、
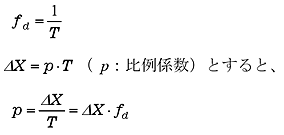 |
|
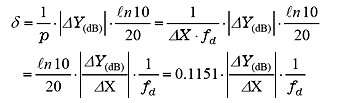 |
(6) |
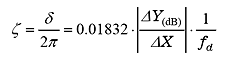 |
(7) |
( fd は周波数スペクトルから求めます。またFFTアナライザーによっては ζ を自動的に計算できます。)
2-3 半値幅法による減衰比の算出
後述するように、減衰比 ζ が小さい場合には振動系は共振特性を示しますが、その共振周波数付近の周波数/振幅特性から減衰比または損失係数、Q 値を算出することができます。
|
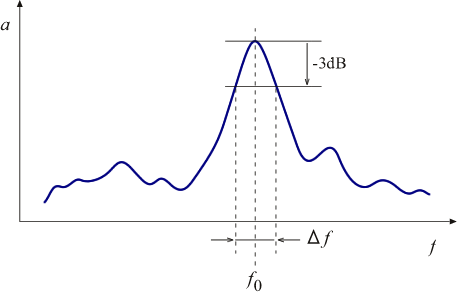
図3 半値幅法 |
図3のような周波数/振幅特性において、振幅のピーク周波数 f0 と、ピーク値より 3 dB 下がった点の周波数幅 Δf から、次式によりQ 値、損失係数 η および減衰比 ζ を求めることができます。
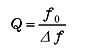 |
(8) |
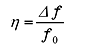 |
(9) |
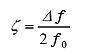 |
(10) |
振幅で −3 dB すなわち![]() は、エネルギーでは
1/2 になるので、この算出方法を半値幅法といいます。
は、エネルギーでは
1/2 になるので、この算出方法を半値幅法といいます。
【注意】
半値幅法によって減衰比を求められるのはζの値が小さい(せいぜい0.1以下)場合に限られます。言い換えると、周波数/振幅特性が図3のようなはっきりした単峰特性を示す場合には半値幅法で減衰比や減衰係数をもとめることができます。(式(10)の導出は【補足】「半値幅法の計算式導出」を参照)
減衰比、対数減衰率は機械や構造物の振動特性の評価指数や設計パラメーターとして使われており、損失係数は制振材などの評価指数としてよく使われています。また Q 値は電気系や機械共振の特性を評価する場合に用いられます。
なお、損失係数の大きな材料の減衰係数を求める場合には、1秒間の減衰量から求める減衰率法やインピーダンス法などが用いられます。制振材料の性能測定については下記に詳しく解説されています。
■ 小野測器技術レポート「制振材料とその性能について」
http://www.onosokki.co.jp/HP-WK/c_support/newreport/damp/damp_index.htm