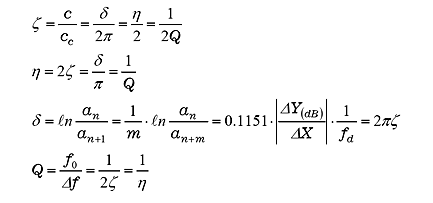4. 関係式のまとめ
5. おわりに
機械が稼働する際に振動は避けられない現象である以上、振動を許容レベル以下に抑えることは機械設計において重要なポイントです。とりわけ共振という現象は、例え小さな外力であっても大きな振動を引き起こすことがあり、十分な注意が必要です。共振周波数(固有周波数)と強制振動の周波数を離すことができれば良いのですが、現実には固有周波数が稼働領域内にあることも多く、設計者にとって頭の痛い問題です。
本稿で説明したように、共振の挙動は減衰によって大きく変わってきます。従って、予め適切な減衰を組み込んでおくことで振動を許容レベル以下に抑えるといった設計も可能です。また問題となっている機械や構造物の振動を低減する場合においても、ダンパーなどの減衰要素を付け加えることはよく行われています。その際には、本稿で説明した減衰に関する知識が基本となります。ここで取り上げた振動モデルは1自由度系で、加えられる外力も正弦波という単純なモデルですが、実際の機械や構造物はもっと複雑な系であり、外力も不規則な波形です。また減衰比の値も振幅や状態によって変化する場合があり、実際の振動解析は簡単ではありません。しかし機械振動の基本はここで説明した1自由度系モデルであり、振動のおおよその挙動は本稿で説明した知識で説明できる場合も多いので、解析や対策を考える際の糸口となるはずです。
以上、減衰比を中心に減衰をあらわす係数が持つ意味とその求め方について簡単に解説しました。本稿の内容は機械や構造物の設計者にとっては当たり前の知識ですが、振動が専門でない方が振動対策を考える際の参考になれば幸いです。
【補足】 半値幅法の計算式導出
最大振幅の式(22)は振幅倍率の式(21)に共振周波数の式を代入することで得られます。
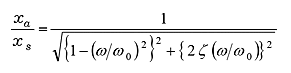 |
(21) |
共振周波数の式![]() より 、これを式(21)の
より 、これを式(21)の![]() に代入すると;
に代入すると;
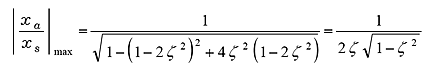 |
(22) |
式(21)、式(22)より、振幅が最大振幅の![]() となる周波数を求めると;
となる周波数を求めると;
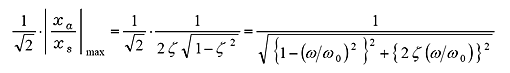 |
(28) |
整理すると;
|
(29) |
これを解くと;
|
|
(30) |
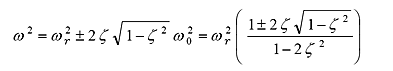 |
(31) |
ζ ≪ 1 とすると、ζ 2 ≒ 0 よって;
|
|
(32) |
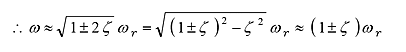 |
(33) |
![]() とすると;
とすると;
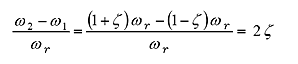 |
(34) |
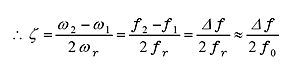 |
(35) |
上記に示すように、半値幅から減衰比ζを求める計算式は ζ ≪ 1 とした場合の近似式なので、精度よく計算できるのは ζ が 0.05 以下、多少の誤差を許容する場合でもせいぜい 0.1 以下までです。
【参考】 構造物や機械の減衰比
実際の構造物や機械の減衰比は概ね次の値です。
| 鉄骨建物 | 0.003 〜 0.04 |
| 中低層ビル(10階以下) | 0.005 〜 0.12 |
| 高層ビル | 0.02 〜 0.1 |
| 鋼製タワー | 0.002 〜 0.03 |
| コンクリート製タワー | 0.01 〜 0.02 |
| 道路橋 | 0.02 〜 0.05 |
| 吊り橋 | 0.002 〜 0.08 |
| 大型乗用車のサスペンション | 0.1 〜 0.3 |
| 小型乗用車のサスペンション | 0.2 〜 0.5 |
| オートバイのサスペンション | 0.35 〜 0.45 |
【参考資料】
-
「振動を制する」鈴木浩平(オーム社)
-
「自動車工学全書11」(山海堂)