5. 半値幅法
外力 F で振動する 1 自由度系の周波数応答関数 H (jω)は、その変位量を X 、動バネ定数を k 、 粘性減衰係数を c 、質量を m とすると
|
|
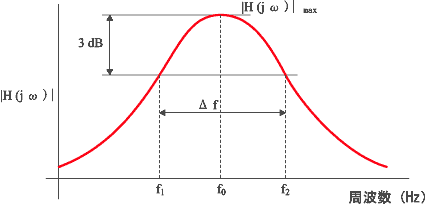
となる。 この周波数応答関数の振幅の最大値を|H|2 max 、この時の角振動数を ω0 とし、ω0 付近で振幅が |H|2 max の 1/2 (振幅のパワーが半分)となる点の振動数を ω1 、ω2 とすると、損失係数は次式で示される。
実際の試験では,周波数応答関数のピーク値から 3 dB 小さい点の周波数 f 1 、f 2 を読み取り、また共振周波数 f 0 から制振性能を求める方法が一般的である。
|
|
従って、実用的には次の式を使う
|
|
また、f 0 を使わない式として次の式を使う
|
|
※ 半値幅法以外に、n dB 幅法を採用してもよい。 この場合の補正値 K は、n dB 幅を採用した場合;
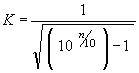 |
となる。 ちなみに 1 dB の K は 1.9652 、2 dB の K は 1.3076 である。
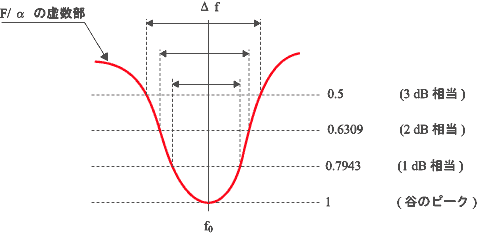
※周波数応答関数の虚数部から半値幅法で損失係数を求める方法
アパレントマス(力/加速度)の虚数部の半値幅(1/√2 ではなく 1/2 )から上の(η = K( f 2 − f 1 )/f 0 )の式から求める。 ただし、F / α の虚数部は全て“負”の値を持ち FFT の CH A に加速度、CH B に入力して、その谷(信号を逆に入力して α/F の山から測定しても良さそうであるが、この両者の虚数部は全く異なるものでひっくり返しても一致しない)の値を −X とすると、f 1 、f 2 は 次の値になる位置で求める。
| 補正値 | |
| -X/1.259 の時(A = 1 dB 相当) | K = 1.965 |
| -X/1.585 の時(A = 2 dB 相当) | K = 1.308 |
| -X/2 の時(A = 3 dB 相当) | K = 1.000 |
(倍率は異なるが周波数応答関数の MAG の時と同じ補正値である)
|
|
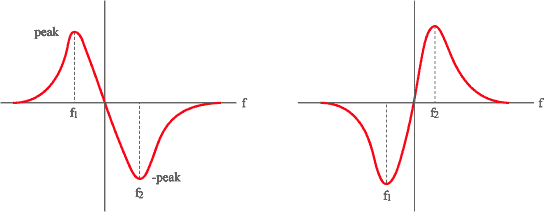
※周波数応答関数の実数部から半値幅法で損失係数を求める方法
|
|
|
| アパレントマス(F/α)の実数部 | スティフネス(F/X)の実数部 |
上記いずれの場合も
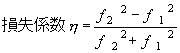 |
の式で計算を行う。
6. 減衰率法
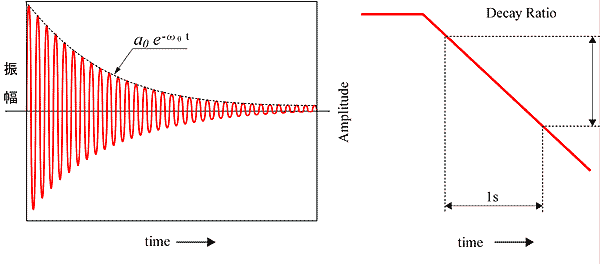
1 自由度系が外力を受けて定常振動している場合、この外力がなくなると、振動は徐々に減衰してゆくが、このときの振動振幅の包絡線は、
で表される。a0 は初期条件により決まる定数である。 この包絡線の 1 秒あたりの減衰量 D (dB / sec)は、
|
|
となる。したがって、
より、損失係数を求めることができる。 ただし、ω0 = 2 πf0 である。
同様の考え方で、振動が 60 dB 減衰するのに要する時間 T60 を測定して
より、損失係数を求めることもできる。 この方法は、残響時間法と呼ばれている。これらの方法は、一般的には減衰が小さい場合に利用され、振動減衰波形をレベルレコーダのような対数アンプを通して表示すると包絡線に比例した直線がえられるので、この直線の傾きから減衰率を測定する。 また、ヒルベルト変換を利用して減衰率を測定する方法も有効である。
|
|
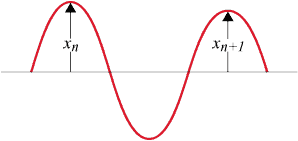
減衰波形から、損失係数を求める場合、減衰開始直後や減衰後半の波形が一定値に漸近していく点の傾きを採用してはならない。また、減衰波形が低次の振動モード等の影響を受けて、きれいな直線にならない場合は、フィルターリングを行う。また、減衰正弦波のある時の振幅値と次の振幅値を χn 、χn+1 としてその自然対数値を対数減衰率と言い、金属材料の減衰能を表す値としてよく使われる。
|
|
|
|
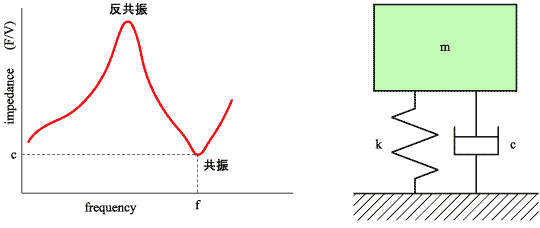
7. インピーダンス法
減衰の大きな材料の損失係数を測定する場合、半値幅法では精度のよい半値幅の測定が行えない場合があり、この場合はインピーダンス法が有効な手法とされている。強制振動をしている
1 自由度系の機械インピーダンス (F / V) の振幅を |z| とすると、共振点では ![]() より、|z|= c となり、インピーダンスは粘性減衰係数を表すことになる。ただし、V は振動速度を表す。したがって、損失係数は次式より求めることができる。
より、|z|= c となり、インピーダンスは粘性減衰係数を表すことになる。ただし、V は振動速度を表す。したがって、損失係数は次式より求めることができる。
なお、質量 m は, 厳密には μ∫Wi2 dx ( μ は単位長さ当たりの質量、Wi は i 次の振動モードの基準関数) から求める。また、同様な方法として, 機械コンプライアンス(X / F) から損失係数を求めることができる。1 自由度系が強制力( f = f0 ejwt ) を受けて振動している場合、ばね を g(1+ η j) としてコンプライアンスを表すと
となる。 ここで式の実部、虚部をそれぞれ R、I とすると g および η は
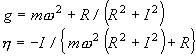 |
より計算できる。
|
|
|
|
インピーダンス
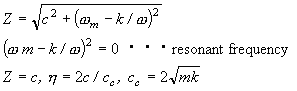 |
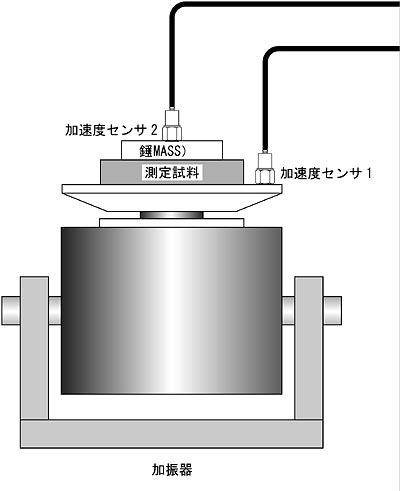
実用的には下記のシステムの場合次の式が用いられる。
|
|
で計算する。 ここで
| f0 : 共振周波数(Hz) M : 試料重量(錘下)+上部錘重量(kg) h : 試料の厚み(m) A : 試料面積(m2)(錘下) E : ヤング率(N/m2) |
|
|
損失係数は加速度センサー1、2の比(振動伝達率)を通常使用し、半値幅法で計算する。
8. 非共振法
半値幅法および減衰率法等は、いずれも共振点または共振点付近で損失係数を測定するもので共振法とも呼ばれているが、ここで示す手法は任意の周波数で損失係数を求めることができる。
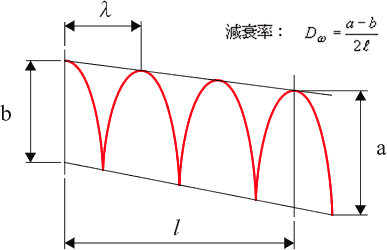
この試験法は、長いはりの試験片の一端を砂に埋め、他方を加振器で加振して、はりに生ずる定在波または進行波より波長 λ (m) および振動減衰 D (dB/m) を測定し, 次式より損失係数を求める方法である。
|
|
|
|