1. 制振
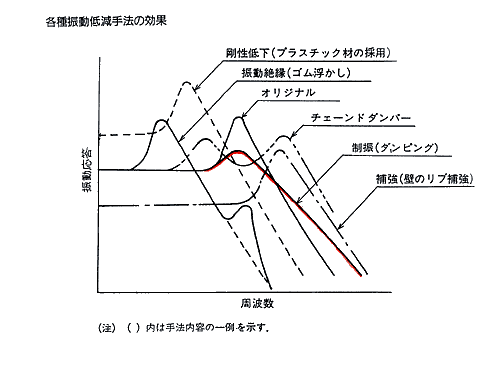
“制振”とは固体表面の振動の振動エネルギーを熱エネルギーに変換し、固体表面の振動を小さくする技術である。これに対して“防振”は振動源と被振動源の間の振動伝達率を小さくすることで振動の遮断に相当する技術である。制振と明確に区別する必要がある。制振は固体表面の振動を低減するばかりでなく、固体表面から放射される固体音を低減させることができる。特に振動面の共振点近傍の振動低減に効果を発揮する。この制振技術は振動対策技術として古くから研究されてきているが、最近の静穏化対策技術への応用として、最近最も注目され研究が進められる一方、制振材料の開発が活発化している。
|
|
2. 制振材料
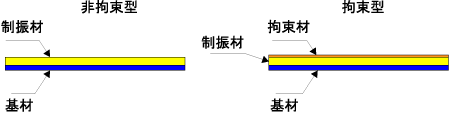
基材(鋼、木、コンクリート、プラスチック等)に樹脂系、ゴム系、アスファルト系、金属系 等の粘弾性材料(流体の持つ流動性を示す“粘性”と固体の持つ復元性を示す“弾性”の両特性をかね持った材料を粘弾性材料という)の制振材を貼り合わせたものを制振材料と言い、その貼り合わせ方法によって“非拘束型(基材+制振材)”と“拘束型(基材+制振材+拘束材)”に分けられる。非拘束型としては制振材単品(両面テープが添付されているものもある)が市販されている。 拘束型の代表は制振鋼板とも呼ばれ市販されている。
|
|
3. 損失係数
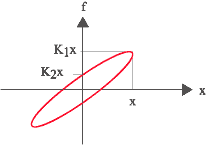
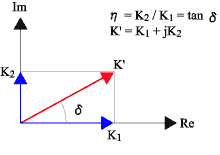
損失係数 η は制振材料の制振特性の評価指標の一つで、損失係数の本来の意味は振動応答系に減衰があると、その応力・歪み線図(あるいは荷重・変位線図)は図1のように一つのヒステリシスを描く。このヒステリシス曲線から、最大変位 χ における力 f = K1 χと、零変位に おける力 f = K2 χを測定して η = K2 / K1 から損失係数ηを求めるところからきている。 また、K1 を実数部、K2 を虚数部で表した図2の表現方法の場合には、K ′を複素弾性率、K1 を 貯蔵弾性率、K2 を損失弾性率と呼ぶ。
|
図1 |
図2 |
制振性能を表す量としては種々あって、電気、機械、物理などの専門分野によって使用される量が異なるが、各量の間には簡単な関係が存在する。これらの関係は表1 のようになる。
| ζ | η | K | Δ | D | Δf | Q | ψ | |
| ζ | − | 2 ζ | ω Rζ | 2 π ζ | aω R ζ | ω R ζ / π | 1/2 ζ | 4 π ζ |
| η | η/2 | − | ω R η /2 | π η | aω R η /2 | ω R η /2π | 1/η | 2 π η |
| K | K/ω R | 2K/ω R | − | 2 π K / ω R | a K | K /π | ω R /2K | 4 π K / ω R |
| Δ | Δ /2 π | Δ / π | ω N Δ /2π | − | aω N Δ /2π | ω N Δ /2π | π /(Δ - Δ 2) | 2 (Δ - Δ 2) |
| D | D/a ω R | 2D/a ω R | D/a | 2 π D /a ω N | − | D /aπ | a ω R / 2D | 4 π D /a ω R |
| Δf | π Δf/ω R | 2 π Δf/ω R | π Δf | 2 π 2 Δf/ω N | a π Δf | − | ω R 2 π Δf | 4 π 2 Δf/ω R |
| Q | 1/2 Q | 1/ Q | ω R / 2 Q | π / Q | a ω R / 2 Q | ω R / 2 π Q | − | 2 π / Q |
| ψ | ψ / 4 π | ψ / 2 π | ω R ψ / 4 π | ψ/2 | a ω R ψ / 4 π | ω R ψ / 4 π2 | 2 π ψ | − |
![]()
表1
| ζ : | 減衰比、粘性係数Cと臨界粘性減衰常数=2 √km との比 |
| η : | 損失係数、ばねと粘性抵抗を含めて弾性項を k(1+iη) と複素表示した場合の損失を示す |
| K : | 減衰常数、振動減衰の |
| Δ : | 対数減衰率、振幅が減衰する場合、隣り合う振幅の比の自然対数 |
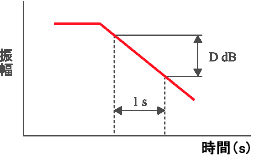
| D : | 減衰度、減衰振動で 1 秒当たりの減衰量をdB表示したもの 残響時間(信号が 60 dB 減衰する時間) T = 60 / D で求められる |
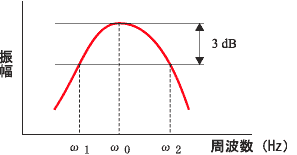
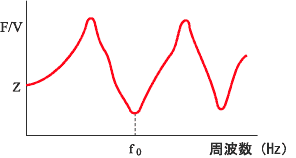
| Δf: | 半値幅、共振付近で周波数を変化して描かれる 共振曲線最大値の 1 / √2 を示す周波数の幅 |
| Q : | キュー、振動系が共振する場合、この共振の鋭さを表す量で、振動系のエネルギー と、その振動を持続するため、外部から与えられる1サイクル当たりのエネルギー の 2 π 倍 |
| ψ : | 固有減衰容量、振動系で失われる1サイクル当たりのエネルギーと、系に蓄えられるエネルギーとの比 |
4. 制振性能の測定法
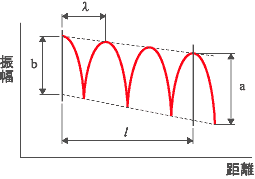
制振性能を表す指標の中で最も一般的なのが、損失係数ηである。代表的な損失係数の測定法は、半値幅法、減衰率法、機械インピーダンス法がある。これらの測定法はいずれも共振周波数付近で測定する共振法であるが、一般的ではないが非共振法もある。 下記は、測定法を整理したものである。
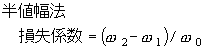 |
 |
 |
 |
 |
 |
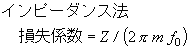 |
|
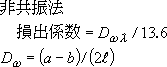 |
 |