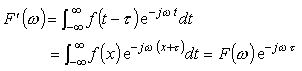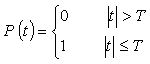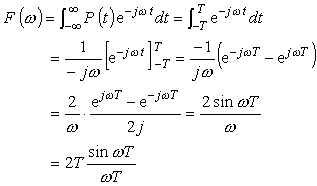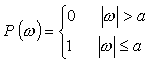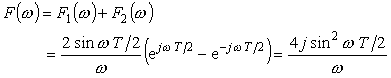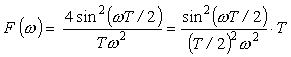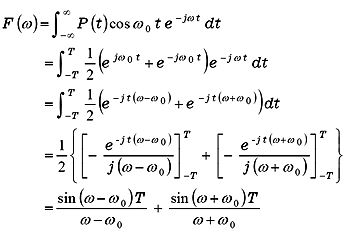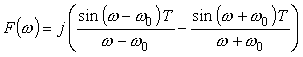5.2 基本的な波形のフーリエ変換・逆変換
次に基本的な波形のフーリエ変換・逆変換を見てみましょう。f (t)、F (ω) = R (ω) + j I (ω) がどのような形となるかを理解してください。まずはじめに、フーリエ変換・逆変換の特性を見てみましょう。
(1)対称性
f (t) のフーリエ変換を F (ω) とすると;
|
|
(式5-17) |
|
|
(式5-18) |
より、![]() を入れ替えると、式
5-17、5-18 より;
を入れ替えると、式
5-17、5-18 より;
|
|
(式5-19) |
の関係が導かれます。この式 5-19は、フーリエ変換、逆変換の対称性を表す式になっています。
(2)平行移動(進み・遅れ)
f (t) がτだけ移動した f (t -τ) のフーリエ変換 F (ω) は、t - τ = x と置くと;
|
|
(式5-20) |
と F (ω) に e -jωτ を掛けたもの、すなわち e -jωt は円運動を表していますので、周波数領域で ωτ だけ位相がずれた波形となります。例えば、τ = 1 s ずれた f (t -τ) は、周波数領域ではF (ω) に比べて、1 Hz では 2π、2 Hz では 4π、4 Hz では 8π と、周波数に比例した位相遅れとなります。
(3)Fourier 核といわれている関数
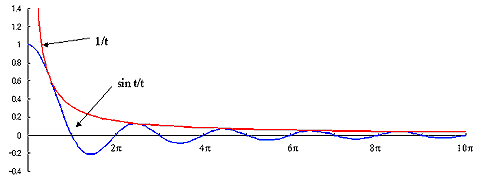
フーリエ変換の基本的な関数で Fourier 核と呼ばれている ![]() を図 5-3に示します。
を図 5-3に示します。
|
図5-3 |
この波形は、f (t) = 1/t に接した波形で、フーリエ変換ではよくでてくる基本式ですので記憶に留めておかれると良いと思います。
5.3 基本的な関数のフーリエ変換
ここまでの内容を基本的な関数に適応させて考えてみます。
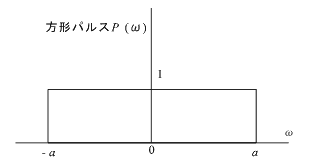
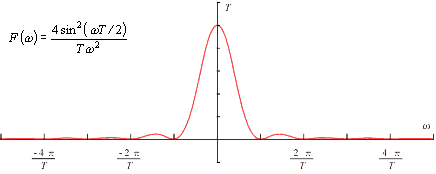
(1) 方形パルス Pt のフーリエ変換
|
|
(式5-21) |
のフーリエ変換は:
|
|
(式5-22) |
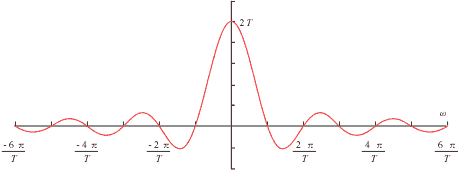
この関係を図示すると次のようになります。
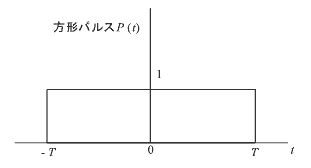
図5-4 |
|
図5-5 |
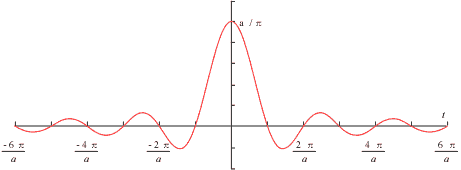
(2) 周波数領域で方形パルスの逆変換を考える
対称性を表す式 5-19 より、式 5-21、式 5-22 の ω → -t、T → a を入れ替え、2π で割ると:
|
|
(式5-23) |
この式の逆変換は;
|
|
(式5-24) |
を得ることができます。
この関係を図示すると次のようになります。
|
図5-6 |
|
図5-7 |
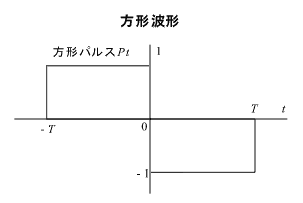
(3) 方形波形のフーリエ変換
下図 5-8のような方形波形を考えます。-T から 0 までは先の式 5-21 と 5-22 での図 5-4 の方形パルスの T を T/2 にし、位置が -T/2 移動したものと考えると、この範囲 PT/2 のフーリエ変換は T を T/2、移動分は式 5-19 より、e jωT / 2 を掛ければよいので:
|
|
(式5-25) |
同様に 0 から T までを考えるとそのフーリエ変換は、
|
|
(式5-26) |
-T から T までを考えると、そのフーリエ変換は、F1 (ω) と F2 (ω) の和になり:
|
|
(式5-27) |
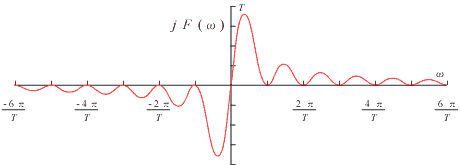
今までは j が付かないので実数部のみです。これには j が付いているので、これは、虚数部のみになります。これを図示すると図 5-9 のようになります。
|
図5-8 |
|
図5-9 |
(4) 三角パルス波
図 5-10 のような三角パルス波 qt は、図 5-8 で Y 軸を 1/T にしたものを積分した波形なので、フーリエ変換は式 5-27 に 1/T・1/jω を 掛けて求められます。 すなわち:
|
|
(式5-28) |
これを図示すると図 5-11 のようになります。
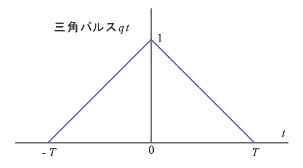
図5-10 |
|
図5-11 |
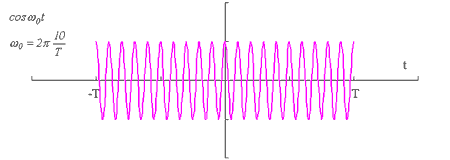
(5) 時間 -T 〜 T で切り取られた cos ω0t
cos ω0 t を -T 〜 T で切り取ったデータは cos ω0 t に 5-3 項(1)の Pt をかけたもの、言いかえると cos 波形を方形パルスで振幅変調したものと考えられます。
![]() のフーリエ変換は:
のフーリエ変換は:
|
|
(式5-29) |
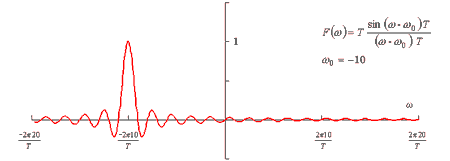
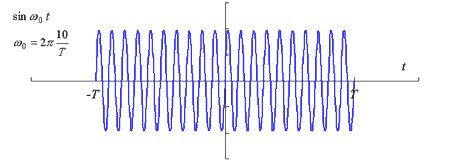
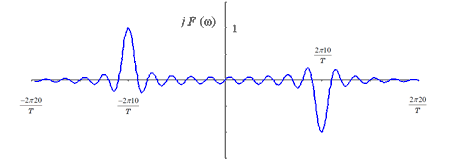
下図5-12は、f0 = 10/T の場合を示します。
|
図5-12 |
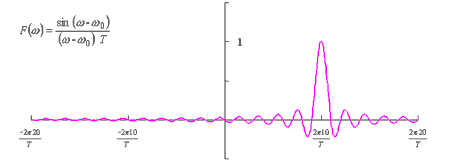
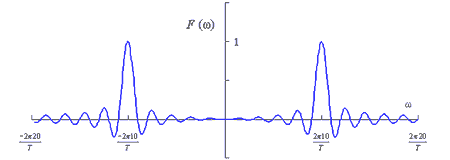
図 5-13-1 は式 5-29 の第1項を、図 5-13-2 は同式の第2項を図示したもので、これは図 5-4 での波形をω0 移動したものとなります。なお、図 5-13-3 に 2つの波形の和、すなわち式 5-29 そのものを図示しました。
|
図5-13-1 |
|
図5-13-2 |
|
図5-13-3 |
(6) 時間 -T 〜 T で切り取られた sin ω0t
先の例と同様に sin ω0t の -T 〜 T で切り取ったデータの変換は:
|
|
(式5-30) |
式 5-30 の第1項と第2項は、先の式 5-29 と同じで、その差を取ったものになります。ただし前に j がついているため、純虚数となることに注意ください。
|
図5-14 |
|
図5-15 |