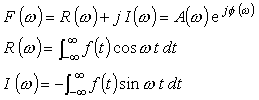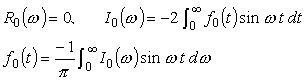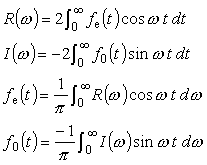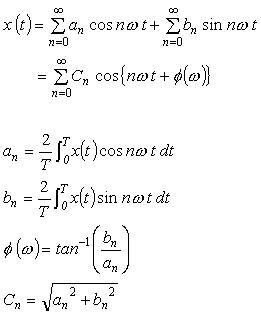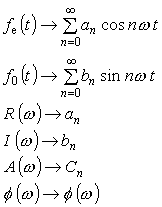技術レポート
FFTアナライザーについて

今一度、フーリエ変換・フーリエ級数に立ち戻り、そこから導き出される性質についての検証から入ります。数式が多数出てきますが、式そのものはあえて覚える必要はありません。数式は FFT アナライザーが内部で処理してくれます。ここでは、式の持つ意味を理解してください。
なお、本項並びに次項で取り上げる内容は、その次に述べるウィンドウ処理（Window function）を理解し、使いこなす上で基礎となる部分です。

最初に、復習を兼ねて、フーリエ変換側からフーリエ級数を考えてみます。

フーリエ変換とその逆変換を表す式は、これまでの話の中で係数 1/T をどのように扱うかによって様々に表現されてきましたが、一般的には；

 

 

で記述されます。

ここで、f  (t) を実関数とすると式 5-1 は；

 

 

と書き換えることができ、R  (ω)、I  (ω) をそれぞれ実数部、虚数部とすると；

 

 

と置くことが出来ます。

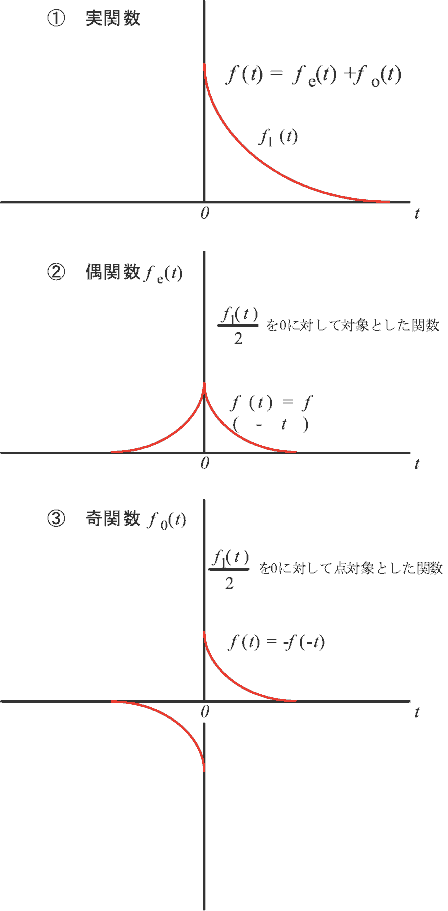
次に下図 5-1のような関数 f₁ (t) 、f_e (t)、f₀  (t) を考えてみます。図 5-1の２番目の関数 f_e (t) は、0を中心に f₁ (t)/2 が対称の関係があり；

 

 

が成り立ち、また次のように表すことが出来ます。

 

このような関数を偶関数と言い、cos ωt はその代表例です。また、図 5-1の３番目の関数 f₀ (t) は0を中心に点対称の関係にあり；

 

が成り立ち、同様に：

 

このような関数を奇関数と言い、sin ωt はその代表例です。

　

　

さらに、この２つの関係から；

 

が成り立つことも理解できると思います。

図からも予想できるように、その積分は；

 

 

となり、偶関数、奇関数の積分がどうなるかを示しています。奇関数の積分は 0 になること（0 になるから計算しやすくなる）に注目してください。

一般に：

　

 

f_e (t) は偶関数ですので f_e (t) cos ωt は偶関数、f_e (t) sin ωt は奇関数となり、このフーリエ変換は式 5-2、式 5-3より；

 

 

です。また、R_e (ω) の逆フーリエ変換は、同様に；

 

 

となります。これは逆にいうと実関数 f_e (t) のフーリエ変換が実関数ならば、f_e (t) は偶関数であることを表しています。

同様に、f₀ (t) についても；

 

 

となり、実関数 f₀ (t) のフーリエ変換が純虚数関数なら、f₀ (t) は奇関数になります。

次に f  (t) について考えると、f_e (t) と f₀ (t) のフーリエ変換をそれぞれ F_e(ω) と F₀(ω) とすると式 5-3は；

 

 

となり、上記フーリエ変換の実関数/フーリエ逆変換の偶関数と同純虚数関数/同奇関数の関係から；

 

 

であることがわかります。以上をまとめたのが次式 5-14です。（フーリエ変換対を ←→ で表しています）

 

 

この式と、前号で示したフーリエ級数とその成分を求める式；

 

 

とを対比させてみると、次の関係を持っていることがわかります。

 

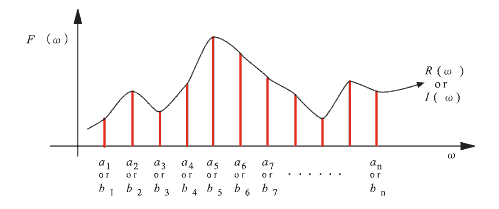
FFT アナライザーでは、フーリエスペクトラムの離散的数値列として a_n、b_n が表示されますが、a_n、b_n を数式で表記したのが R (ω)、I (ω) で、R (ω) が実数部を示し偶関数、I (ω) は虚数部を示し奇関数となります。この関係を模式的に示したのが次図 5-2です。また、a_n² + b_n² = C_n² の C_n² はこの対数を取ってパワースペクトルとして表示され、φ （ω）は位相スペクトルとして表示されることは、前号で説明した通りです。