4.4 Y軸の値
次ぎに FFT アナライザーで表示される Y 軸の値について考えてみます。サンプル値列 x (n) より FFT された第 k 番目のスペクトルを ak、bk とすると;
(1)フーリエスペクトル

(2)パワースペクトル
-1.片振幅表示のスペクトル
-2.全振幅表示のスペクトル
-3.実効値表示のスペクトル
-4.対数表示の片振幅スペクトル
-5.対数表示の全振幅スペクトル
-6.対数表示の実効値スペクトル
(3)位相スペクトル
(4)微分積分
加速度 α、速度 v、変位 x、その周波数を f とすると、加速度、速度、変位は微積分関係にあります。
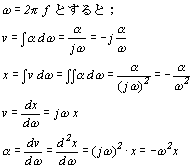
±j や - 符号は、位相差 ±90゜、-180゜を意味しています。
(5)オーバオール
次ページに FFT アナライザーの表示波形を示しながら上述の(1)〜(5)のY軸値について詳しく解説して行きます。
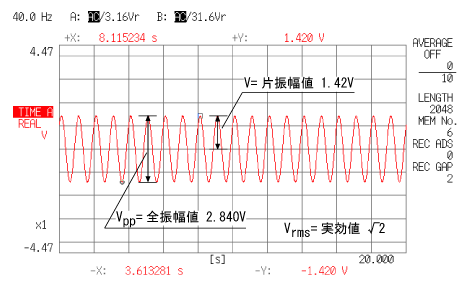
正弦波の振幅を表現する方法として、全振幅値、片振幅値、実効値があります。
<データ 7> |
上のデータ7は cos 波の時間軸波形ですが、振幅の +ピークと -ピークの幅を全振幅値といい、全振幅値の 1/2 の値を片振幅値といいます。また、実効値は、「同一抵抗に消費する電力が同じになる直流の値で表した交流の大きさ」と定義されますので、交流の瞬時値の2乗を1周期に渡って平均した値の平方根に等しくなります。すなわち、交流の瞬時値を x (t) とすると、その実効値は;
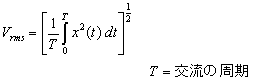
上式で求められ、交流信号が正弦波の時には、その実効値は片振幅値の 1/√2 となります。
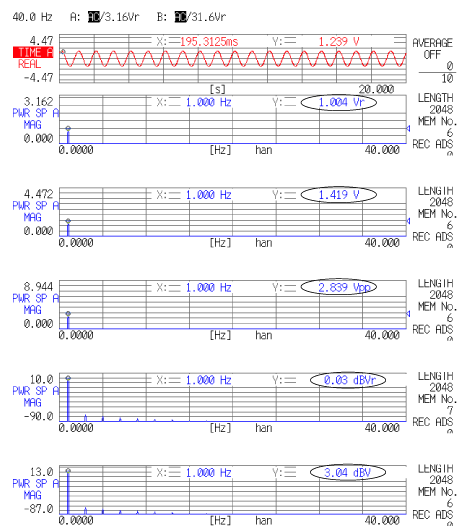
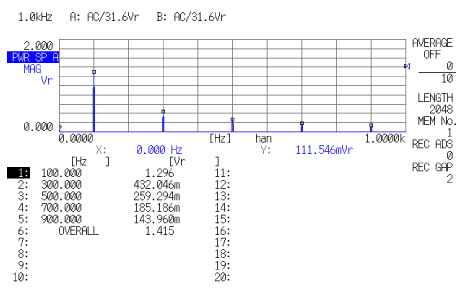
次データ8は、データ7の時間軸波形を FFT し、実効値で表したスペクトルを2段目に表示しています。このデータから入力信号は 1 Hz、1.004 Vrms(実効値)の信号であることが分かります。
<データ 8> |
データ8の3段目には同一波形を片振幅値で現したものを載せています。なお、片振幅値は次のように手計算でも求めることが出来ます。
![]()
4段目は全振幅値として現したもので、同様に計算で求めることが出来ます。
![]()
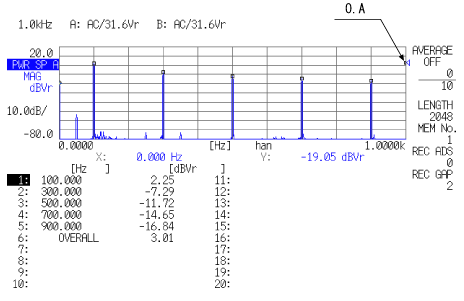
5段目は実効値を対数表示で現したもので先に示した式に従い dB Vrms は;
![]()
6段目は片振幅値を対数表示現したもので、dBV は;
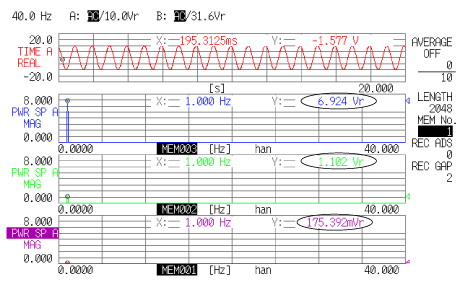
データ9は、スペクトルの積分を説明するためのものです。1段目は入力信号、2段目に実効値表示のスペクトルが表示されています。(スペクトルから入力信号はf = 1 Hz、Vr = 6.924 Vであることが分かります。)
<データ 9> |
3段目は1重積分したスペクトルです。先に示した式により、2段目のスペクトルに 1/jω を掛けたものです。また、4段目に2重積分したスペクトルを示します。1/j は、-90゜の位相遅れを現すので、位相を無視してそれぞれの積分値(大きさ)は次のように求めることが出来ます。
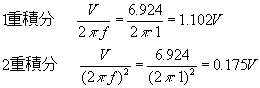
入力信号が加速度 α (m/s2)の時の、速度、変位は、加速度を1重積分、2重積分したものなので、加速度センサーの感度、1m/s2 当たり何Vかを考慮し電圧を加速度に換算すれば、上式より周波数毎の速度、変位を求めることが出来ることになります。
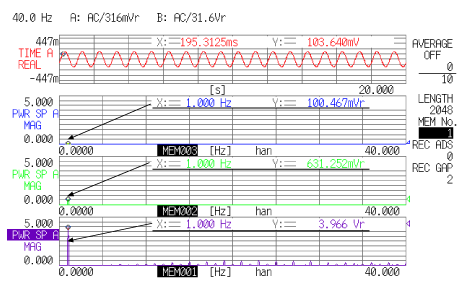
データ10にスペクトルの微分結果を示します。
<データ 10> |
1段目は入力信号、2段目は実効値表示のスペクトルです。このスペクトルから入力信号は 1 Hz、100.467 Vであることが分かります。データの3段目、4段目は、2段目のスペクトルを1回微分、2回微分したスペクトルであり、先の本項(4)微積分の式から、それぞれ jω、(jω)2 を掛けたものとなります。j は +90゜の位相の進みを表しますので、スペクトル(大きさ)を考えると下式より計算できます。
![]()
積分の時とは逆に、入力信号が変位であれば、微分することで速度、加速度を求めることが出来ます。
データ11でオーバオール(O.A)に関して説明します。
オーバオールは、全周波数スペクトルを合成したパワーで、時間領域のパワー(2乗平均値)に一いたします。なお、このパワーはサンプル点数(例えば、2048 点)が対象となっていることを忘れないでください。
オーバオールは次のように求めます。
(1)Y 軸が対数でない場合(データ11-1 を参照)
<データ 11-1> |

データ 11-1 の下段に各スペクトルのピーク点をリスト表示していますが、このピーク値以外はゼロとし、また Hf = 1 として概算のオーバオール値は次のように計算できます。
![]()
なお、オーバオール値は、データ上段右端の 部に表示されます。
(2)Y 軸が対数の場合(データ11-2 を参照)
<データ 11-2> |
(1)と同様に;
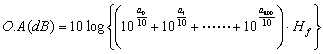
としてオーバオールを求めることが出来ます。
データ11-2 は、データ11-1 を dB 表示したものであり、Hf = 1 としてそのオーバオール値を計算すると次のようになります。
![]()
オーバオールは、実効値を指示する指示計、例えば振動計のメータ指示値や騒音計の指示値などに相当します。
今回の解説はいかがでしたでしょうか。実際に FFT アナライザーに表示される波形を例として取り上げ、時間軸とフーリエ変換されたX軸、Y軸の関係や値の読み方を主に説明いたしました。ご不明の点等ございましたら、ご遠慮なくお問い合わせください。なお、データ採取のため使用したアナライザーは、CF-5220マルチパーパスFFTアナライザーです。 次回は、FFTアナライザーで信号を取り込む際に重要な入力処理に関してお話を進めて参ります。「FFTアナライザーについて」のお話はもうしばらく続きます.........