この関係は、加速度センサーや騒音計からの入力信号を FFT 分析する際に、スケールを m/s2 や騒音計の dB 単位に校正する機能として利用されています。
4.3 データの移動
あるサンプル値列 x1 (n) があり、そのサンプリング値列を l（エル）だけ平行移動させたサンプル値列 x2 (n) に対する FFT の結果は、x1 (n) の FFT の結果と位相の変化が生じるだけで、パワースペクトルは一いたします。
下のデータ４は、上段が 10 Hz の cos 波のサンプル値列、２段目がそのスペクトル、３段、４段目は、それぞれフーリエスペクトルのリアルパートおよびイマジナリパートを表示しています。
|
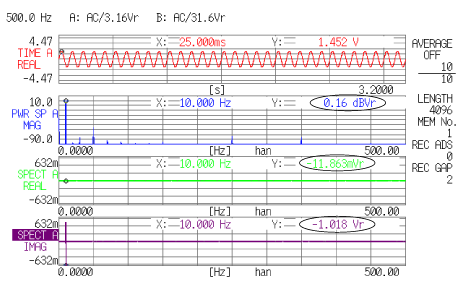
＜データ 4＞ |
また、データ５は、データ４と位相を変えた信号で、上段が 10 Hz の cos 波のサンプル値列、２段目がそのパワースペクトル、３段、４段目は、それぞれフーリエスペクトルのリアルパートおよびイマジナリパートを表示しています。
|
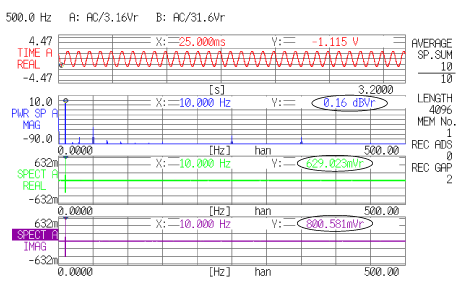
＜データ 5＞ |
データ４と５を比較してみると、パワースペクトルは +0.16 dB と同じ値ですが、リアルパートおよびイマジナリパートの各値が異なります。これは、波形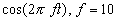
Hzを基準に位相を見るとデータ５は；
より、+51.84（度）の位相差があるためです。この位相関係を表示したのがデータ６下段の位相スペクトルです。
|
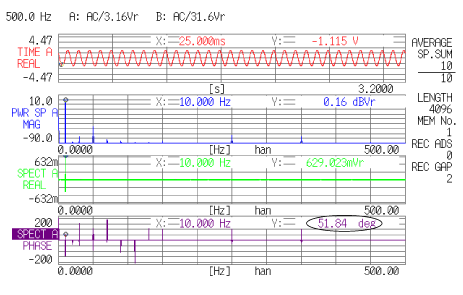
＜データ 6＞ |
このように、DFT の特徴は数学的に示すことができます。DFT では、時間領域での複雑な計算（= 考え方）が、周波数領域では簡単な計算となります。前号 3-4 項式 3-16、17 での DFT、IDFT の中での x (n)、X（k）はそれぞれ数値列であり、e-aj を掛けるか、eaj を掛けるかの違いだけです（a = 2πkn/N）。極論すれば、サンプル列に e-aj を掛ければ DFT、eaj を掛ければ IDFT であるといえます。実際、DFT も IDFT も FFT の手法を利用しているわけです。
ここで、FFT の主な特徴をまとめてみると次のようになります。F[x] をフーリエ変換とすると；
（１）線形結合
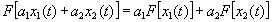
（２）対称性
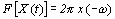
（フーリエ変換X（ω）を波形X（ｔ）とすると、その逆変換はx（-ω）になる）
（３）相似性
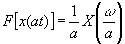
時間軸データを大きくとると（t → at）、周波数分解能は向上する（ω → ω/a）が、その分パワーは分散される。（1 → 1/a）
（４）平行移動
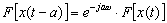
（５）微分
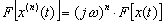
時間領域のn回微分は、現波形のスペクトルに
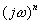をかけたものとなる。
（６）積分
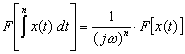
時間領域のn回積分は、現波形のスペクトルに
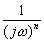を掛けたものとなる。
（７）合成積
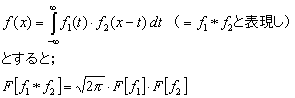
上式は、コンボリューション（畳み込み積分）といわれ、このフーリエ変換は、f1、f2 の個々のフーリエ変換の積となる。なお、この式は、ある信号系の入力と出力の関係を表す式で、周波数応答関数（伝達関数）測定に利用されます。
（８）保存則
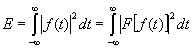
これは、パーシバルの定理で、同一現象であれば、時間領域でも周波数領域でも同じことを表現している根拠となっています。すなわち、左辺は信号 f (t) の全エネルギーを表し、右辺はその全エネルギーが各周波数成分にどの様に分布しているかを表しており、エネルギー保存の法則を示しています。FFT アナライザーでは、オーバオールとして右辺の周波数スペクトルから計算・表示しています。サンプリング定理のため帯域制限していることに注意が必要です。
と置くとわかりやすくなります。
