3.6 フーリエ展開の計算例
本項では、実際にある時間波形の1周期分のフーリエ級数を計算してみます。
下図 3-9 は、サンプル数 N = 12 の1周期波形データから k = 2 の第2高調波のフーリエ係数を計算する手順と、同様な計算を k = 0 〜 6 ※まで行った結果としてのこの波形のフーリエ級数式 3-20 を示しています。(※:サンプリング定理によりサンプル数 N = 12 の場合、分析できる高調波次数 fm = 6 )
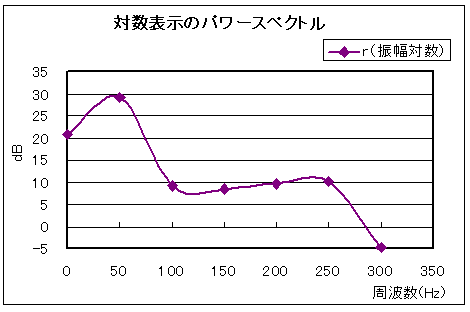
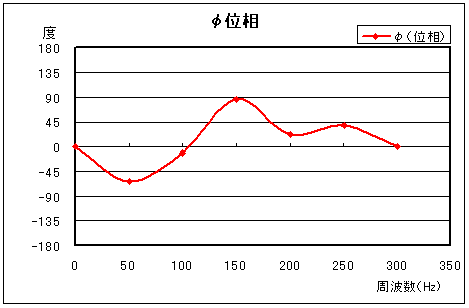
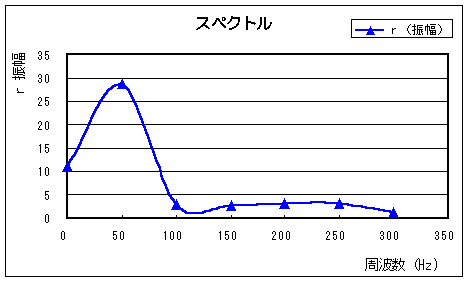
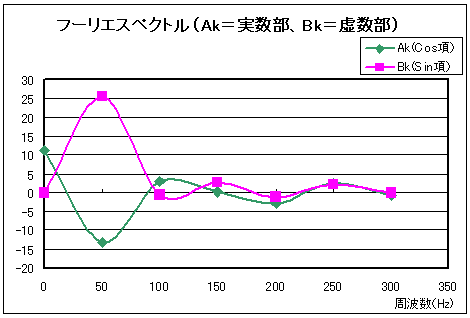
また、その下の図 3-10 は、このサンプリングデータが周期 T = Nh = 0.02 秒(ω0 = 50 Hz)とした場合のFFTアナライザーで表示されるデータを示しています。
このように手計算で行うと高々 12 個のサンプリングデータでさえ、大変な時間がかかってしまいます。FFTアナライザーでは、N を 2n にとる FFT の手法を使い(例えば、1024 = 210 )、こうした計算を短時間で処理し、データをメモリーに保存するとともに、そのデータから時間軸波形やスペクトラム等の波形を表示することで入力された波形が持つ様々な特徴を我々に伝えてくれます。
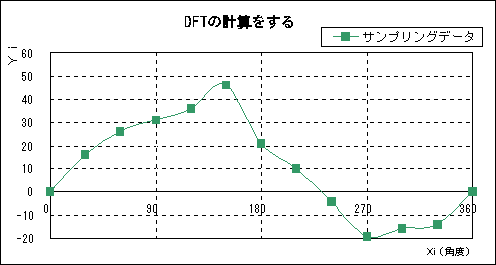
図3-9
フーリエ係数 a0、ak、bk は:
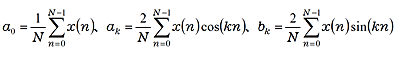
第2高調波の計算テーブル
| n | Xi (角度) | Yi(データ系列) | Cos (2xi) | YiCos (2xi) |
|---|---|---|---|---|
| 0 | 0 | 0 | - | - |
| 1 | 30 | 16 | Cos(60)=0.5 | 8 |
| 2 | 60 | 26 | Cos(120)=-0.5 | -13 |
| 3 | 90 | 31 | Cos(180)=-1 | -31 |
| 4 | 120 | 36 | Cos(240)=-0.5 | -18 |
| 5 | 150 | 46 | Cos(300)=0.5 | 23 |
| 6 | 180 | 21 | Cos(360)=1 | 21 |
| 7 | 210 | 10 | Cos(420)=0.5 | 5 |
| 8 | 240 | -4 | Cos(480)=-0.5 | 2 |
| 9 | 270 | -19 | Cos(540)=-1 | 19 |
| 10 | 300 | -16 | Cos(600)=-0.5 | 8 |
| 11 | 330 | -14 | Cos(660)=0.5 | -7 |
| 12 | 360 | 0 | Cos(720)=1 | 0 |
| Σ | - | 133 | - | 17 |
上表より k = 2 の時のフーリエ係数は;
a0=133/12=11.08、a2=2/N∑x(n)cos(2n)=2.83
と計算できます。同様な計算を k = 0 〜 6 まで行うと、次式を求めることが出来ます。
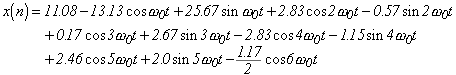 |
(式3-20) |
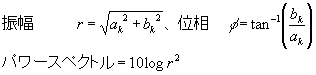
| 周波数 (Hz) |
Ak (Cos項) |
Bk (Sin項) |
r (振幅) |
φ (位相) |
r (振幅対数) |
|
|---|---|---|---|---|---|---|
A0 |
0 | 11.08 | 0.00 | 11.08 | 0.00 | 20.89 |
ω0 |
50 | -13.13 | 25.67 | 28.83 | -62.91 | 29.20 |
2ω0 |
100 | 2.83 | -0.58 | 2.89 | -11.58 | 9.21 |
3ω0 |
150 | 0.17 | 2.67 | 2.68 | 86.36 | 8.55 |
4ω0 |
200 | -2.83 | -1.15 | 3.05 | 22.11 | 9.70 |
5ω0 |
250 | 2.46 | 2.00 | 3.17 | 39.11 | 10.02 |
6ω0 |
300 | -0.59 | 0.00 | 0.59 | 0.00 | -4.66 |
図3-10
パワースペクトル
位相
振幅
フーリエスペクトル
4.FFTアナライザーの画面の見方
4.1 時間軸分解能と周波数分解能
簡単な波形を実際にFFTアナライザーで分析しながら、先に説明した FFT との関係・FFT の特徴を見て行くことにしましょう。
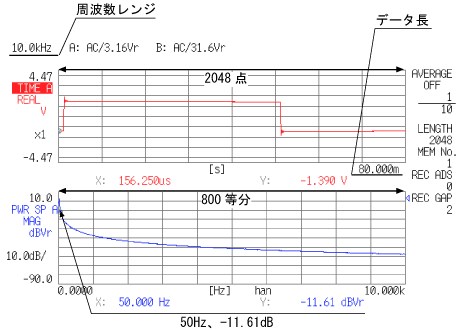
下のデータ 1 は、素性の分からない原波形の1つを周波数レンジ 10 kHz で分析した結果です。原波形に対し、サンプリング時間が短いので、時間軸で表示した場合は原波形が細かく観測されますが、周波数軸では周波数分解能が十分でないためスペクトルが連なった状態(包絡線)になってしまっています
|
<データ 1> |
この時の周波数領域の X 軸と周波数レンジとの関係は次のように求まります。
<時間軸(上側のデータ)>
原波形を時間軸分解能 ΔT = 約 0.039 ms ごとにサンプリングした 2048 点分のデータ 80 ms 分を表示しており、これが基本周波数Tになります。

<周波数軸(下側のデータ)>
この時間軸波形を DFT することで、0 Hz 〜 10 kHz 迄 12.5 Hz 毎 800 個のスペクトルデータが表示されます。

この 12.5 Hz は、基本周波数 80 ms の逆数(1/T)になっています。次表にサンプル数、データ長、周波数分解能の関係をまとめましたので参考としてください。
サンプリング点数 |
データ長T(秒) |
周波数分解能 1/T |
|---|---|---|
256 |
|
|
512 |
|
|
1024 |
|
|
2048 |
|
|
4096 |
|
|
<f:周波数レンジ>
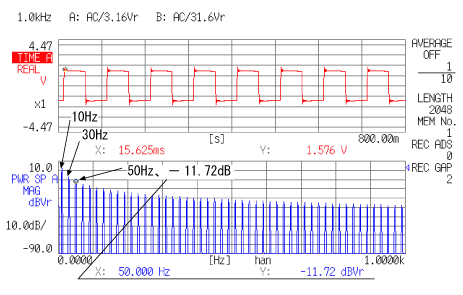
次にデータ2を見てください。これは、データ1と同じ波形を周波数レンジ 1 kHz で分析した結果です。時間軸分解能は悪くなりますが*、逆に周波数分解能が 1.25 Hz と良くなったため、基本波 10 Hz の奇数倍の高調波成分が詳細に読みとれます。結果から原波形は 10 Hz の矩形波であることが分かります。(*注:信号周波数に比べサンプリング周波数が十分高いため時間軸波形は目立って悪くなっておりません。)
|
<データ 2> |
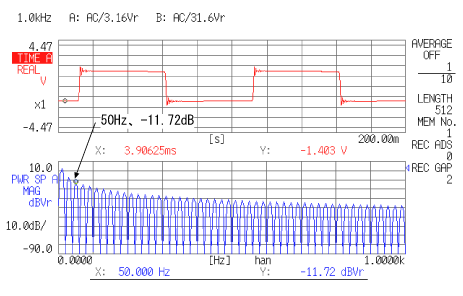
では、同じデータ波形を4分の1のサンプリング点数 = 512 点、周波数レンジはデータ2と同様の 1 kHz で分析したデータ3を見てみましょう。データ2に対し、データ長が 800 ms から 200 ms と短くなったので、周波数分解能が 1 kHz の 1/200 の 5 Hz となり、不確実性が現れてきます。
|
<データ 3> |
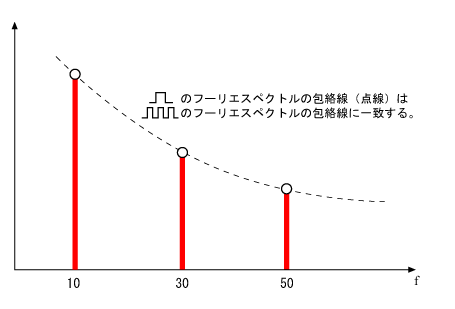
データ1〜3の各スペクトラム波形(下側)に 50 Hz のスペクトル値を示していますが、ほぼ同じ値となっていることが読みとれると思います。これは、前号の図 3-10 の G で説明したように、DFT のスペクトルの包絡線は原波形のスペクトルに一致する事を示唆しています。
|
図4-1 |