3.4 離散的フーリエ変換
FFTアナライザーでは、時間波形 x (t) はサンプリング間隔 h の飛び飛びのデータ(離散的データ)として扱われます。 サンプリング間隔 h でサンプリングされた有限のデータ N 個のサンプル値系列を x (n) (n = 0、.....N-1)とすると、このデータに対しても同様にフーリエ変換が成り立ちます。フーリエ展開は、「時間波形 x (n) にある波形 e-j2πft を掛けて、その1周期分を積分すると、ある波形の振幅を求めることが出来る」ことから、式 3-9b を参考にこの離散的データを式に当てはめると;
 |
より、第 k 次高調波のフーリエ変換式は;
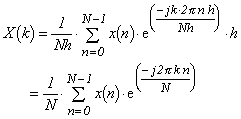 |
(式3-16) |
で表され、この式 3-16 を離散的フーリエ変換(DFT: Discrete Fourier Transform)といいます。また、この式は式 3-7b と同じように式 3-11 の関係式が成立します。同様に、離散的逆フーリエ変換(IDFT: Inverse Discrete Fourier Transform)は:
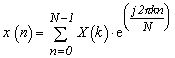 |
(式3-17) |
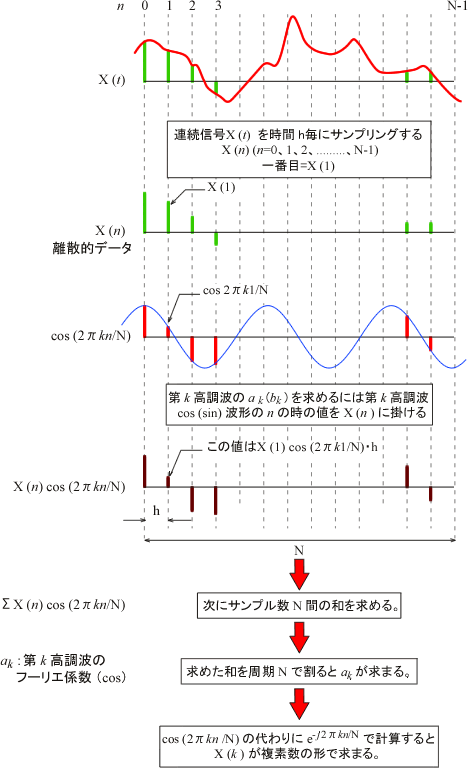
で表されます。なお、DFTの式3-16を概念的に下図 3-5に示しましたので参考としてください。
3.5 サンプリング定理
では、高調波kは何処まで計算できるのでしょうか。
元の波形が解るには、その波形の周波数の2倍以上の周波数でサンプリングする必要があります。これをサンプリング定理といいます。 今、周期 T の波形でサンプリング数が N 個の場合を考えてみます。この時、サンプリング時間 h とその周波数 fs は;
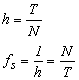 |
(式3-18) |
ですので、サンプリング定理より分析できる周波数 fm は;
|
|
(式3-19) |
すなわち、第 N/2 高調波までとなります。
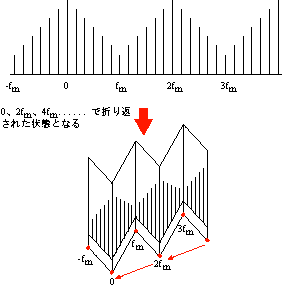
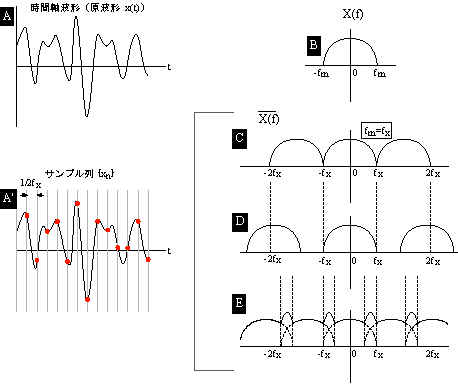
0〜fm 迄に帯域制限された波形を fs でサンプルし、DFT の計算をすると、周波数 -∞ 〜 +∞ のスペクトルが得られます。図 3-6 に周波数 -fm 〜 4fm 迄のスペクトルを模式的に図示します。
図3-6 |
この図に見られるように、得られるスペクトルは丁度 fm の整数倍で手紙を折り返したように同じ値が繰り返されます。また、fm 〜 2fm 迄に帯域制限された波形を同じ fs でサンプルし DFT しても、同様に図 3-6 のようになり、実際には存在しない 0 〜 fm の成分が計算上求められてしまいます。これをエリアジング現象(折り返し歪み)といい、この時の fm をナイキスト周波数と呼びます。得られたスペクトルの 0 〜 fm だけを見ると、原波形が 0 〜 fm なのか fm 〜 2fm なのかの判断が出来ません。そこでFFTアナライザーでは、予め fm 迄に制限するローパスフィルター(エリアジングフィルターという)を通し、fm 以下の信号に確定してサンプリング定理を満足させるようにしています。また、このローパスフィルターが充分減衰する周波数を得るのに fm + α の周波数まで考慮する必要があることから、FFT アナライザーでは fm の 1/1.28 迄のスペクトルしか表示しないようにしています(図3-7)。
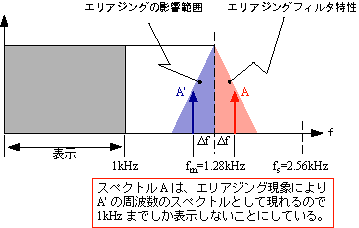
図3-7
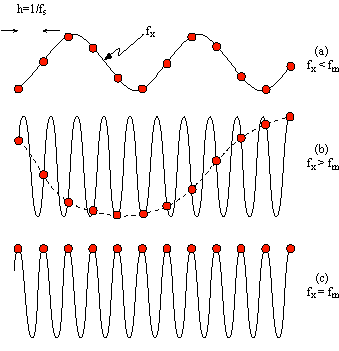
なお、サンプリング定理を時間波形から考えてみたものを図 3-8 に、エリアジングフィルターの ON/OFF によるFFTアナライザーでの表示波形を図 3-9a、bに示します。
図3-8 |
|
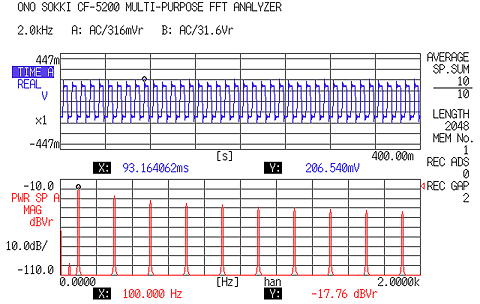
エリアジングフィルターの効果により、エリアジング現象が発生していない。ただし、時間波形の矩形波は、このエリアジングフィルターにより高周波成分がカットされるため波形が影響を受け、完全な矩形波にはならない。 図3-9a |
|
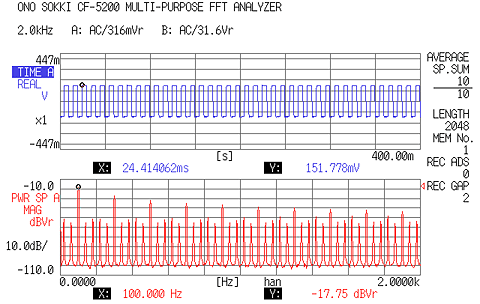
エリアジングフィルターが掛かっていないため、時間波形は本来の矩形波だが、FFT の結果は、エリアジングが発生し、本来はない周波数成分が現れている。 図3-9b |
だいぶ話が複雑かつ数学的になってきましたが、ここまでの内容はお解りいただけましたでしょうか。
ここで、少しイメージ的な概念を交えてフーリエ級数・変換、DFT並びにサンプリングについてをFFTアナライザーの視点から整理してみたいと思います。城戸健一著「デジタル信号処理入門」より引用して、説明します。
図 3-10 をご覧ください。「A」波形は、ナイキスト周波数 fm 以下に帯域制限された無限に繰り返される時間波形であり、「A」の周波数スペクトルを求めると「B」になり、これは原点を中心として ±fm に分布し、その範囲外はゼロとなります。次に、「B」のスペクトル X (f) が周波数軸上で 2fx という周期で無限に並ぶものとし、これを X (f) とすると;
図3-10 |
-
fx = fm の時には、「C」のスペクトル波形
-
fx < fm の時には、「D」のスペクトル波形
-
fx > fm の時には、「E」のスペクトル波形
が考えられます。ここで、「E」のスペクトル波形は、各スペクトルが重なり、エリアジングが発生した状態です。また、「C」および「D」のスペクトル波形では -fm 〜 +fm の範囲では x (t) のスペクトル X (f) と同一となります。別の見方をして、x (t) を 2fx でサンプルしたサンプリング列 xn を考えます。この時の xn スペクトルは;
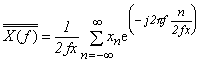 |
(式3-20) |
これは、「C」「D」「E」を式で表したものです。すなわち、fx に帯域制限された連続波形 x (t) を 2fx でサンプリングし、その無限のサンプル列 {xn} のデータより、スペクトル X (f) を求め、その -fx 〜 +fx の周波数範囲を見ると、それは x (t) の周波数スペクトル X (f) そのものとなります(「C」「D」)。
X (f) を逆フーリエ変換すると x (t) が得られますから 1/(2fx) 毎のサンプル値系列は連続波形 x (t) を表すのに充分な情報を持っています。サンプリング周波数より原波形の周波数の方が高いと、エリアジングにより「E」のように重なり合ったスペクトルになり、このスペクトルは X (f) と違ってしまい、従って x (t) も再現できなくなります。
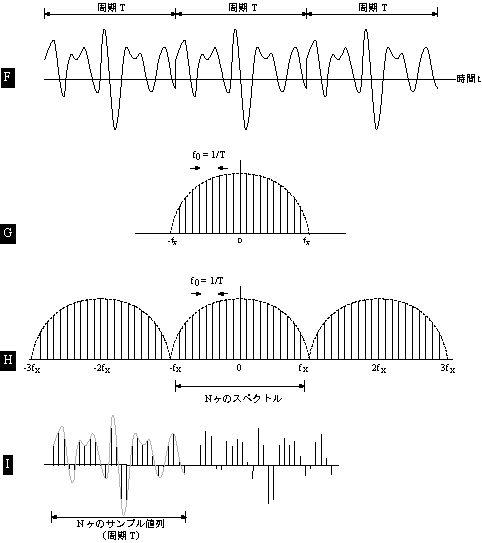
ここまではフーリエ変換に関しての話です。 次に、「A」の波形が、「F」のように周期 T で無限に繰り返されているとすると、その波形をフーリエ展開した周波数スペクトルは、周波数軸上に 1/T の間隔で並ぶ線スペクトルになります。この波形の周波数成分は fx 以下に制限されているので、「G」のようなスペクトルとなり、この線スペクトルの包絡線は「B」の連続スペクトルと一いたします。「G」のスペクトルを「C」「D」と同様に 2fx の周期で無限に繰り返されているスペクトル「H」を考え、「H」を逆フーリエ変換した時間波形は「I」のように、周期 T で無限に繰り返されるサンプル値系列になります。つまり、時間波形も、スペクトルも、周期的に無限に繰り返すサンプル値系列になります。この関係を表したものが式 3-16、3-17 の DFT および IDFT です。式 3-16、3-17 の;
|
は、Sin、Cos 波形と同様、ある周期で繰り返し同じ値を取る周期関数ですから、DFT、IDFT が図の「H」「I」を表していることがご理解できると思います。
また、0 〜 fx のスペクトルが正しく求まれば、情報として充分であることもお解りいただけることとことと思います。なお、参考用として、スペクトルから連続波形に戻す式を示します。サンプル列{xn}は;
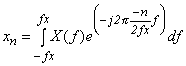 |
(式3-21) |
で表され、そのスペクトル X (f) の -n 項目のフーリエ係数が xn となります。また、サンプル値系列{xn}より、連続した原波形 x (t) は次式にて求めることが出来ます(図3-11参照)。
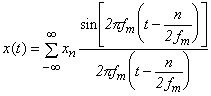 |
(式3-22) |
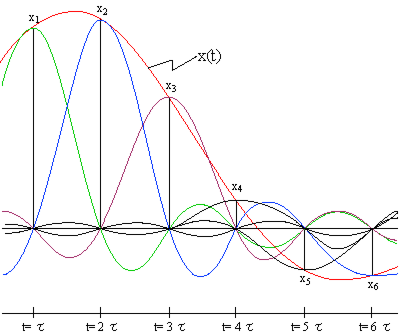
図3-11
では、最後に DFT についてをまとめて、今号のフーリエ級数・フーリエ変換の説明を終えることにします。
まとめ
周期 T で無限に繰り返す信号 x (t) がある周波数以下に帯域制限されているとすると、周期 T の信号をサンプリング定理に従った一定の間隔 h でサンプリングされた N 個の離散的サンプリング列{xn}から、1/T = 1/Nh 毎の DFT を行うことにより、離散的スペクトル(線スペクトル)X (f) を求めることが出来、また IDFT により、離散的サンプリング列{xn}を再生することが出来る。
FFT アナライザーは、時間領域では 0 〜 N-1 個のサンプリング列を時間波形として、また周波数領域では 0 〜 fm/1.28 までの周波数スペクトル(線スペクトル)を表示しています。