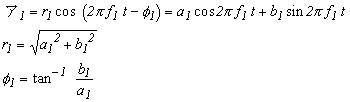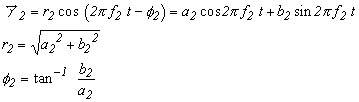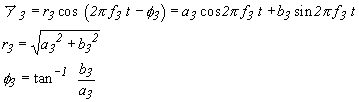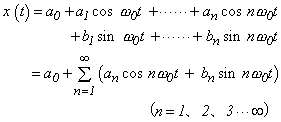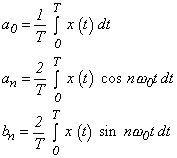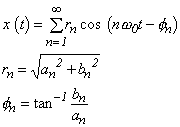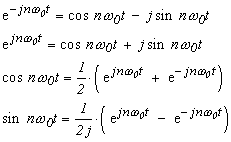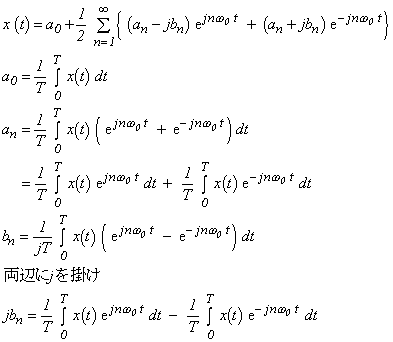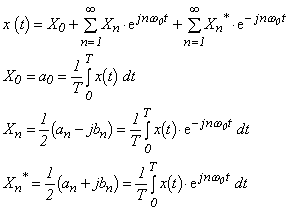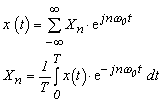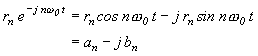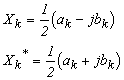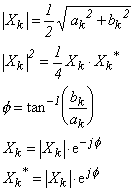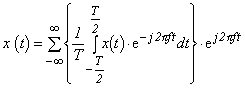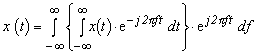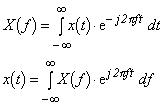3.フーリエ級数とフーリエ変換
時間領域で周期的に変化する波形は、フーリエ級数を使って表すことができることを前号で述べました。 本項では、実際にこうした周期波形をフーリエ級数・フーリエ変換を使用して表してみます。
3.1 フーリエ級数
まず初めに、前号図 1-1 の「ア」の音について考えてみることにしましょう。「ア」の声は「ア1」 、「ア2」、「ア3」...に分解できました。また、「ア1」の波形は位相差を持った Cos 波として前号で説明したように:
|
と表せます。同様に「ア2」「ア3」も:
|
|
となります。
「ア」の音 x (t) は「ア1」、「ア2」、「ア3」.....の合成波ですから:
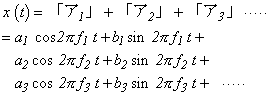 |
ここで、f1、f2、f3、..a1、a2、a3..b1、b2、b3、..をそれぞれfn、an、bn、(n = 1、2、3、...∞)として整理すると:
|
|
(式3-1) |
となります。
この「ア」の声を表す式 3-1 を、次に掲げるフーリエ級数の定義式 3-2 と比べて見ると非常によく似ていることに気づかれると思います。「ア」の成分 f1、f2、f3、..は、基本周波数を f0 とすると、f1 = f0、f2 = 2f0、f3 = 3f0、..となり、第1、第2、第3、..高調波( f0 の整数倍の周波数)に該当します。前号図 1-2「ア」の分析例では、T = 160 ms( f0 = 6.25 Hz)に取っていますので、図の f1 = 106.25 Hz = 17 f0(第17高調波)、f2 = 34 f0、f3 = 51 f0 になります。f1、f2、f3、..に該当しない高調波は暗騒音など、「ア」とは別の信号要素と考えることが出来ます。
ここからお解りのように、前号 2-2 項以降、これまで見てきた考え方が、フーリエ級数そのものなのです。 では、このフーリエ級数の定義式を見てみましょう。
時間領域で周期的に変化する波形は、波形の周期をTとおくと、
-
基本周波数 f0 = 1/T
-
基本角周波数 ω0 = 2<span style="font-family:'GFS Didot'">π</span>f0
となり、フーリエ級数として次のように表すことができます。
|
|
(式3-2) |
ここで、前号 2-6 項の Cos、Sin の掛け算と、その面積を使うと式 3-2 の各成分を求めることが出来ます。
|
|
(式3-3) |
a0 は直流成分、an と bn は角周波数が nω0 の Cos 波と Sin 波の振幅であり、フーリエ係数といい、また、an と bn を一組にして、フーリエ係数対といいます。
ここまでをまとめてみましょう。
上式3-2は、次のように解釈できます。
nω0 t(n =1,2,3,...∞)は基本角周波数 ω0 の1倍、2倍、3倍、......の高調波で、その nω0 t の成分の波形は
|
で表され、そのときのフーリエ係数 an、bn は式 3-3 で求められます。また、下図 3-1 に示した an と bn との関係から、式 3-3は次のように表すことが出来ます。
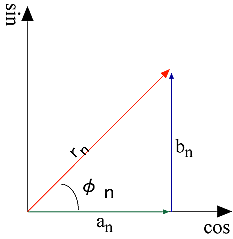 図3-1 |
|
|
(式3-4) |
ここで、rn、φn は、各々第 n 次高調波の振幅および位相です。
FFT アナライザーは、計算結果としてのフーリエ係数 an、bn をメモリーに記憶し、この an、bn から周波数 fn の振幅 rn と位相 φn を演算します。この演算の結果として、周波数 fn と振幅 rn との関係を表したのが、スペクトル表示であり、同様に周波数 fn と位相 φn との関係を表したものが位相スペクトルとなります。また、an、bn から式 3-2 を用いて時間波形に戻すことが出来ます。なお、スペクトルは大きさだけの量なので(位相情報<φ>を持っていない)、スペクトルデータだけでは元の波形に戻すことは出来ません。FFT アナライザーの機能の1つにフーリエ変換データから時間波形を求める(逆フーリエ変換)手法がありますが、これを行うには、位相情報を持つフーリエスペクトル(実数部と虚数部からなる)を記憶しておく必要があります。また、元波形を記憶しておくと、このデータから再度 FFT する機能も持っています。
*実数部・虚数部については次項で説明します。
3.2 フーリエ級数を複素指数関数で表す
FFTアナライザーにより演算・処理される各種関数の内、フーリエスペクトルや伝達関数等の表示の際に「リアルパート」、「イマジナリーパート」という表現が現れます。これは、フーリエ級数を複素平面(ガウス平面)で表現する際に現れるもので、関数表現の一手法であり、各々のパートはそれぞれ重要な意味を持っています。本項では、フーリエ級数をオイラーの公式を使って複素指数関数表示に変換し、この「リアルパート」「イマジナリーパート」の概念を説明します。
少し、難しくなりますが、下に載せた図 3-3 だけは理解しておいてください。なお、複素数・指数については、ここでは詳しくは説明しませんので、興味ある方は専門書を参照ください。
オイラーの公式は:
|
|
(式3-5) |
このオイラーの公式で、n、e、j はそれぞれ;
-
n : 円周率 3.141592....
-
e : 自然対数の底で、e = 2.71828..。e t は微分しても積分しても“e t ” d/dt (e t ) = e t
-
j : j 2 =−1 となる値
ご存じのように数には実数と虚数があり、j のつかない数を実数、j の付く数を虚数といいます。
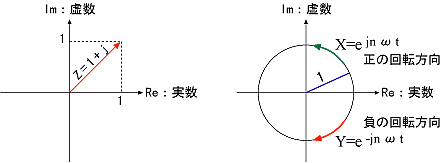
複素平面(ガウス平面)上で、複素数 Z = 1+1 j は図 3-2(a)のように表されます。
また、X = ejnωt は 図 3-2(b)のように複素平面上で半径 = 1 の円を表し、時間とともに反時計方向(正の方向)に毎秒 nω の速度(角速度)で回転しています。
これは、前号の式 2-7 および 8 でのボールの軌跡を表す Cos、Sin の両式を1つの式で表しているといえます。
同様に、Y = e-jnωt は時計方向(負の方向)で回転しています。
X および Y は、実数軸(Re 軸)に対して対称の関係があり、Y は X の、X は Y の共役複素数といいます。
共役複素数は、Z* のように「*」を付けて表示します。
|
|
上式 3-5 をフーリエ級数式 3-2、3-3 に代入し、整理すると:
|
|
(式3-6) |
となります。ここで、(an - jbn)と(an+jbn)に注目し、X0、Xn、Xn* をそれぞれ:
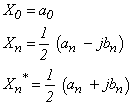 |
と置くと、式 3-6 は:
|
|
(式3−7) |
| (式3-7a) | |
| (式3-7b) | |
| (式3-7c) |
と書き換えることが出来ます。
上式 3-7b で n = 0 とした場合を考えると、e0 = 1 より、式 3-7b の右辺は式 3-7a の右辺と一致することから、n を n = 0〜∞ として、式 3-7を次のように書き換えることが出来ます。
|
|
(式3−8) |
また、式 3-7c の n を n =−1〜-∞ とすると、式 3-7b の右辺(n = 1〜∞)と一致することから、Xn* は Xn の n = -1〜-∞ の時として扱うことが出来ます。従って、以上をまとめると式 3-7、7a、7b、7cは:
|
|
(式3-9a) |
(式3-9b) |
となり、非常にすっきりした形で表すことが出来ます。
この式 3-9a を複素指数表示のフーリエ級数、式 3-9b を複素指数表示のフーリエ展開と呼びます。
オイラーの公式の ejnω0t、e-jnω0t は、Cos、Sin から成り立っているので、今まで見てきた Cos、Sin の周期性を引継いでいるとともに指数の性質を持っています。ejnω0t や e-jnω0t を、それぞれ Cos、Sin と置き換え、例えば、式 3-9b を Cos に置き換えると式 3-3 の an の式に相当し、また;
|
の関係式から、フーリエ係数の Cos 項と Sin 項は、複素数表示の実数部と虚数部になっていると考えるとフーリエ級数とその複素数表示との関係が理解し易くなります(図 3-1 と図 3-3 を比べてみてください)。
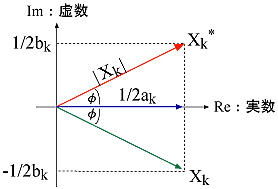 図3-3 |
さて、この時の第 k 高調波は次のように表されます。
|
|
(式3-10) |
Xk* は Xk の共役複素数となっており、横軸を実数部(Re)、縦軸を虚数部(Im)の複素座標で表すと、図 3-3 の様に、Re 軸に対し対称となります。
図 3-3 は、前号第 2-6 項図 2-9 と同様に考えることが出来るので、次式 3-11 が成り立ちます。
|
|
(式3-11) |
この時、Xk はフーリエスペクトル、1/2ak はフーリエスペクトルの実数部(Re:リアルパート)、1/2bk は同虚数部(Im:イマジナリーパート)といい、また |Xk|2 はパワースペクトルと呼ばれます。なお、FFT アナライザーでのフーリエスペクトルは、ak、bk を、パワースペクトルは 4|Xk|2 を表示します。 これは、図 3-1 の rn、an、bn で表すと便利であるからです。
3.3 フーリエ変換
式 3-9a は、フーリエ級数ですから、「ある波形が周期的に続く」時間波形を表す式です。この式に式 3-9b を代入すると次式 3-12 を得ます(なお、計算をやり易くするため、ここでは波形の 0 〜 T を -2/T 〜 2/T に置き換えています)。
|
|
(式3−12) |
ここで、周期性の無い波形でも扱えるように周期Tを -∞ 〜 +∞ に拡張することを考えてみます。式 3-12 で 1/T の T を大きくしていった極限の、非常に小さい周波数である df と置くと:
|
|
(式3-13) |
上式で{}内を X (f) と置くと:
|
|
(式3-14) |
(式3-15) |
式 3-14 はフーリエ変換を、式 3-15 は逆フーリエ変換を表します。フーリエ変換式 3-14 では 1/T が消えてしまいますが、式 3-15 の逆フーリエ変換側に移ったと見れば、このフーリエ変換・逆変換のペアは、先の式 3-9 でのフーリエ展開・級数のペアと対応していることが解ります。式 3-14 と式 3-15 は似ているので間違えないようにしてください。X (f) は周波数領域を、x (t) は時間領域を表しています。
なお、フーリエ級数では、スペクトルは飛び飛びの高調波として表されましたが、フーリエ変換では、周期を無限大に拡張していますので、基本周波数 f0 (= 1/T)は非常に小さな値となり、連続した周波数のスペクトルとなります。
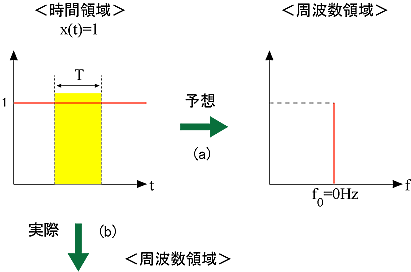
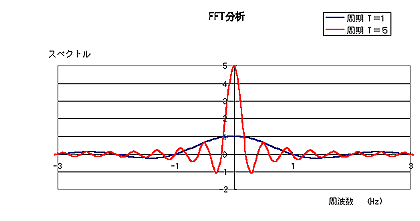
ここで、x (t) = 1 のフーリエ変換を考えてみましょう。 無限に続く 1 の値の内、ある時間分 T を切り取り、それ以外はゼロ(0)と見なしてフーリエ変換してみます。 図 3-4 に T = 1 の場合と、T = 5 の場合を示します。予想は図 3-4a ですが、図 3-4b と比べるとかなり異なります。しかし、T を大きく取った方が波形の幅が狭く、振幅値も大きくなり、図 3-4a に近づいています。この相違が生まれるのは、見えない部分を勝手に 0 としたためで、当然 T を大きく取った方が波形全体の特徴を明確に表します。ここからお解りになるように、フーリエ変換は波形を切り取る時間 T(時間分解能という)が大きいほど周波数分解能(= 1/T)が高くなり、詳細なスペクトルを知ることが出来ますが、逆に波形を切り取る時間が小さい(時間軸分解能が高い)と、周波数分解能は荒くなり、概略のスペクトルしか解りません。このように、フーリエ変換は、時間分解能と周波数分解能の間に不確定性といわれる性質を持っています。FFT アナライザーでは、この時間長 T はデータ長(サンプル数)として、目的に応じての変更が可能となっています。
|
図3-4 |