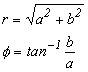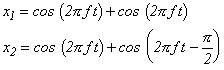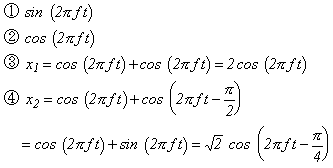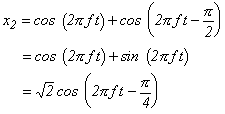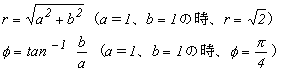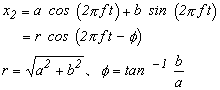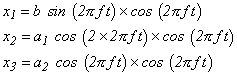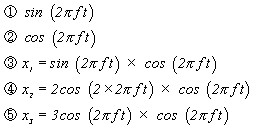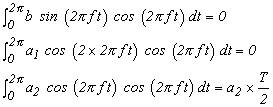2.2 波の軌跡
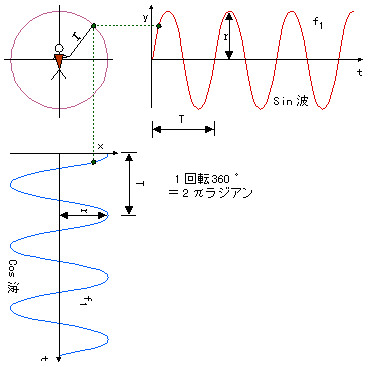
図2-4
|
(式2-2) |
また、1秒間に何回転したかを表す周波数fは次式 2-3 で与えられます。
|
(式2-3) |
では、t 時間後のそれぞれの影の軌跡を数式で表すとどうなるのでしょうか。
|
(式2-4) |
ここで、ボールが下図 2-5 のような角度 φ の位置にいる時を考えると、式 2-4より:
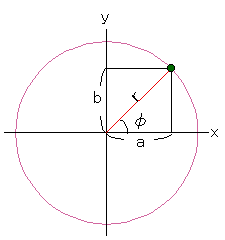
図2-5
|
(式2-5) |
となり、a、b、r は直角三角形の各辺なので次式 2-6 が成り立ちます。
|
(式2-6) |
このように考えてくると、ボールの位置は式 2-5 の(a、b)でも、式 2-6 での(r、φ)でも特定できることがわかります。ボールは円運動ですから、何回転しても φ の位置に来れば両式は成り立ちます。
物理現象は、波動現象と言い換えられるほど、周期性を持っています。sin と cos は、こうした周期性を持った物理現象を説明する数式に Tangent(=tan)とともに三角関数として使用されます。
ここで、φ の位置をスタート点(この時 φ を初期位相という)とした時を考えてみます。この時、式 2-4は:
|
|
(式2-7) |
|
|
(式2-8) |
と表すことが出来ます。
ボールの運動軌跡を表す式は、式 2-7、式 2-8 どちらでもよいのですが、Sin 波は π/2 だけ位相が遅れている Cos 波ととらえることができ、また、物理的背景もあり、Cos 波を基準とする式 2-7 が一般的に使われます。
次に、波形表現に関係して、FFT での波形解析の際よく出てくる重要な用語とその意味について解説します。
2.3 時間差と位相
山に向かって声を発すると、暫くして山彦のエコーが聞こえてきます。声を発してからエコーが戻ってくるまでの時間差を位相差で表すとどうなるか考えてみましょう。
波形の周期を T(周波数 f)、時間差を τ、位相を φ とすると:
|
|
(式2-9) |
例えば、先の「ア」の波形で「ア1」の周波数を 106 Hz として、エコーが戻ってくるまでの時間差 τ = 0.001 秒であるとき、位相はおおよそ 0.21 π = 38.1 度の遅れがあることになります。同じ時間差 τ = 0.001 秒でも「ア2」の場合には、周波数が 212 Hz とすると、76.3 度の遅れとなります。このように、時間差が同じでも周期 T(周波数)が違うと位相も違ってくることに注意が必要です。
2.4 電気角と機械角
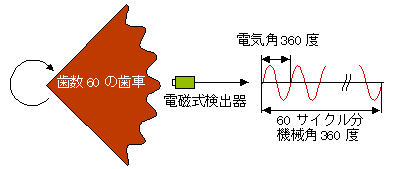
振幅、周波数、位相と関連して、電気角と機械角についての違いを理解しておくことも重要です。 今 60 枚の歯を持つ歯車に電磁式検出器を取り付け、歯車が毎分 600 回転(r/min)している場合を考えます。歯車が 1 回転すると、電磁式検出器からの信号は、正弦波 60 サイクル分が出力されます。ここで信号正弦波の1周期を 2π rad(360 度)にとって表現した位相を=電気角と言い、また歯車の1回転を 2π rad にとった位相を=機械角と言います。
|
図2-6 |
図2-6のように;
-
信号正弦波の周波数 f = 600 r/min /60s×60 ギヤー歯数 = 600(Hz)
-
歯車1回転の周波数 f0 = 600 r/min /60s = 10(Hz)
となります。信号正弦波と歯車の1周期は角度で表すと同じ 2π rad なのですが時間は:
-
検出器信号の周期 = 電気角表示の周期 = 2π = 1/600(秒)
-
歯車1回転の周期 = 機械角表示の周期 = 2π = 1/10(秒)
です。
電気角は電気信号の1周期を、機械角は物体の回転の1周期を基準にしています。回転体の現象を分析するときには、電気角と機械角の関係に注意して周波数分析データを評価する必要があります。 FFTアナライザーでは、電気角を使用します。
2.5 回転次数と高調波
回転次数という言葉は、回転数を基準に分析する場合によく使います。上述した歯車の回転を基準(基本周波数)に考えると信号正弦波は歯車の基本周波数の 60 倍の周波数になっています。これを「第 60 次高調波」といいます。特に回転機械では歯車の回転周波数 10 Hz を回転1次、信号正弦波 600 Hz を回転 60 次と「回転」の言葉をつけて言い表します。
高調波という言葉は、基本波の周波数に対し、その整数倍の周波数のことをいいます。例えば、「ア」の基本波「ア1」の周波数が 106 Hz の時、その第 2 高調波「ア2」の周波数は 212 Hz であるというように使います。最近、電源の高調波歪みの分析がなされていますが、これも 50 Hz あるいは 60 Hz を基本電源周波数として、その整数倍の高調波成分がどの程度か、周波数での振幅・位相を分析するものです。
2.6 波形表現 <波形の和(合成)>
次の波形の和(合成)を考えてみます。
|
|
(式2-10) |
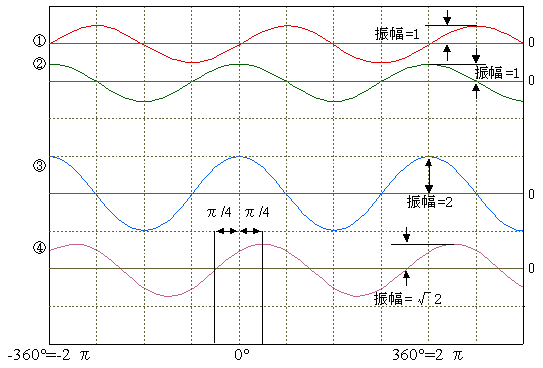
各々の合成波形は下図 2-7 の ③、④ように周波数は同じでも振幅、位相がそれぞれ異なる波形となります。
|
|
まず、x2 を考えます。x2 は三角関数の公式から;
|
|
(式2-11) |
となります。これは、周波数と位相が同じ cos 波と Sin 波を合成すると、振幅が √2 倍で位相が π/4 遅れた cos 波と同一となることを意味しています。これはまた、次のように拡張して考えることができます。
|
|
(式2-12) |
とし、cos 軸にその係数 a を sin 軸に b を取ると、図 2-8 のようになります。
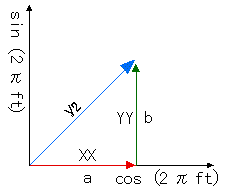
図2-8
これは、先の図 2-5 と同じですから、式 2-6 より;
|
|
(式2-13) |
となります。 すなわち;
|
|
(式2-14) |
が成立します。このように、単一周波数の波形(以後単純波形という)は、同じ周波数で係数を a、b とする ![]() 式で表すことができ、この時の係数
a、b が解ると、その合成振幅の大きさ r と位相差 φ を求めることが出来ることになります。 同様に、x1 の合成波形は、
式で表すことができ、この時の係数
a、b が解ると、その合成振幅の大きさ r と位相差 φ を求めることが出来ることになります。 同様に、x1 の合成波形は、![]() の係数
a = 2、b = 0 と見なすことが出来ますから、合成振幅の大きさ r = 2、位相差 φ = 0 となります。 「ア」の声を周波数分析した各成分「ア1」、「ア2」、「ア3」...は、単純波形なので、各波形は、
の係数
a = 2、b = 0 と見なすことが出来ますから、合成振幅の大きさ r = 2、位相差 φ = 0 となります。 「ア」の声を周波数分析した各成分「ア1」、「ア2」、「ア3」...は、単純波形なので、各波形は、![]() で表されることになります。なお、ここでの位相差
φ の基準は
で表されることになります。なお、ここでの位相差
φ の基準は![]() であることに注目してください。
であることに注目してください。
2.7 波形表現<波形の積>
単純な波形は![]() で表現できることを説明しました。本項では、この式の係数
a、b をどの様にして求めるかについて解説します。
で表現できることを説明しました。本項では、この式の係数
a、b をどの様にして求めるかについて解説します。
次の波形の積を考えてみます。
|
|
(式2-15) |
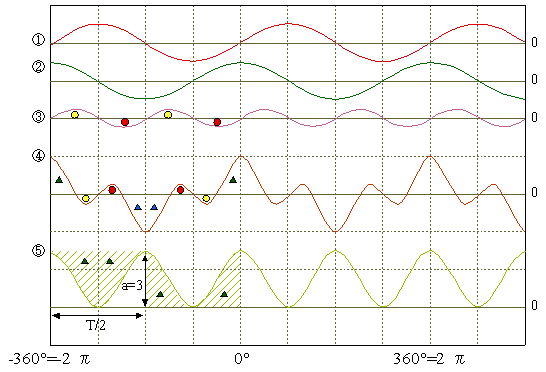
次図 2-9 に、a1 = 2、a2 = 3、b = 1 としたときの各波形を示します。
|
図2-9 |
この図のように、周期性を持った波形の積は、同様に周期性を持った波形となります。 x1 の波形の1周期分(0 から 2π まで)を積分してその面積を見てみましょう。 x1 の波形は、0 を対称にプラス側の面積 ●とマイナス側の面積 ●は同じなので、合計面積はゼロになります。x2 は、第2高調波成分との積を表していますが、この波形の面積合計も同様にゼロになります。しかし、x3 は、マイナス側がないので合計面積 = 振幅 a × T/2 となります。
すなわち:
|
|
(式2-16) |