1. FFTとは
フランスの数理学者 Fourier の発見したフーリエ変換は、理論的にはフーリエ級数をその源としています。 フーリエ級数は、どんな複雑な波形も同じ形を繰り返す周期性を持った波であれば、複数の単純な正弦波(Sin 波)と余弦波(Cos 波)の級数で表現することが出来るという理論です。 この理論を数式で表現したものをフーリエ級数いいます。さらにこの級数を −∞ ~ +∞ まで拡張し、発展させたものがフーリエ変換です。 実際測定しようとする信号はどこまで観測すれば周期性があるとわかるのか不明です。まして無限大時間まで測定するとなると気の遠くなる話になります。 そこで、一般的には観測される波形の内適当な時間分を切り取り、切り取った波形が無限に繰り返される信号と仮定し、この波形に対してフーリエ変換を行います。 当初、このフーリエ変換の計算は、膨大な回数の掛け算計算が必要でしたが、データ数を 2 の n 乗個にとることにより計算回数を少なくする方法が J.W.Cooley と J.W.Tukey により提案されました。 データ数を 1024 とすると、1024 × 1024 = 1048576 回の掛け算が 10240 回に短縮されます。この方法が、Fast Fourier Transform (高速フーリエ変換)といわれ、その頭文字を取って FFT と一般的に呼ばれるようになりました。
1.1 FFTアナライザー
FFT の計算は、具体的にはフーリエ級数の係数(フーリエ係数)を求めることを指します。 FFTアナライザーは、入力された信号波形をデジタル的(離散的)にサンプリングすることにより、データとして記憶し、このデータから FFT を使い、短時間でフーリエ係数を求め、その結果を表示する計測器と言えます。 また FFT の意味が信号を単純な周波数に分解することから周波数分析器、あるいは周波数成分の大きさ(スペクトル)を表しているのでスペクトルアナライザーとも言われています。 例えば、「ア」の声をFFTアナライザーで分析すると、 下図 1-1のように、X 軸に周波数 f、Y 軸にその振幅 r をとったスペクトル波形が表示されます。 このスペクトル波形は、「ア」の声が周波数が f1、f2、f3..... で、それぞれの振幅が r1、r2、r3、..... .の波によって成り立っていることを意味しています。 また、逆な見方をすると、周波数 f1、f2、f3..... 、その振幅が r1、r2、r3、..... の波を合成すると「ア」の音になることを表しています。 下図 1-2 に実際に測定した「ア」の時間波形とそのスペクトルを示します(下:時間軸波形、上:スペクトル波形)。 スペクトル波形の左側にピークとして現れている周波数が f1、f2、f3..... に相当します。 では次に、より具体的な例を元に見ていくこととしましょう。
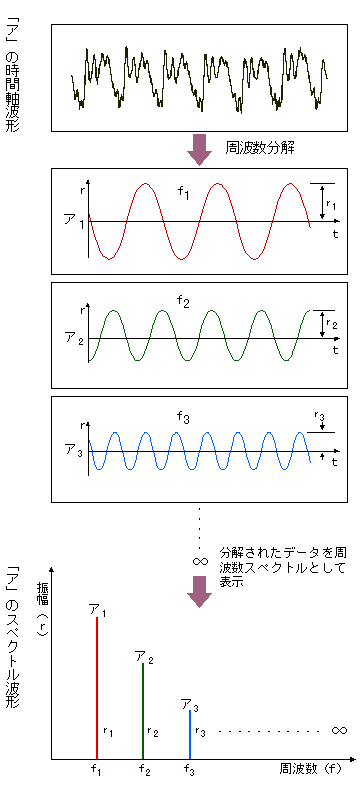
図1-1
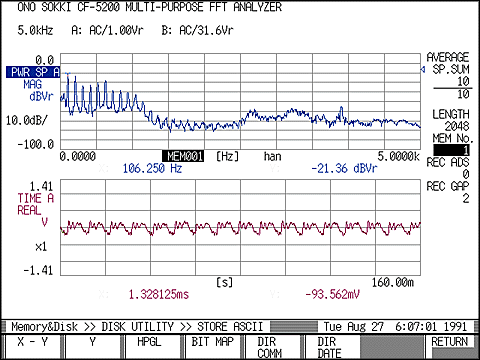
図1-2
1.2 何故FFTが必要か
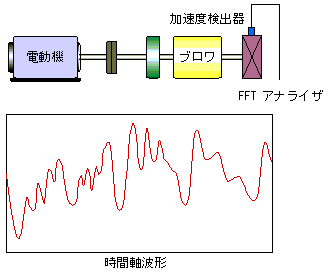
図1-3
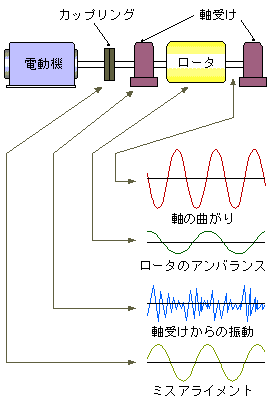
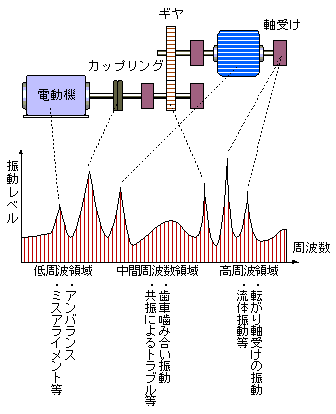
図 1-5
2.波形の表し方(Sin波とCos波)
2.1 振幅、位相、周波数
波形は、振幅と周波数(または周期)、位相(時間差)の3つのパラメーターで表すことが出来ます。
振幅
振幅は波形の大きさを表します。音で考えると、大きな音は大きな振幅を持っています。 物理的現象は、たとえば振動は振動計、音は騒音計、力は荷重計、圧力は圧力計というように、各種センサーで検出します。その信号は、物理量の大きさに比例した電圧の振幅値として出力されます。FFTアナライザーの時間軸波形表示やオシロスコープ、ペンレコーダによる測定は、この電圧出力の時間経過を観測していることになります。
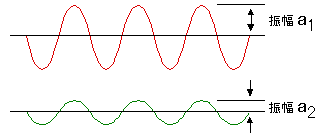
図2-1
周波数
周波数とは、1秒間に繰り返される波の回数を表し、単位は Hz です。周波数を f、周期を T とすると次の関係があります。
| (式2-1) |
音で考えた場合、周波数の高い波形は高音、周波数の低い波形は低音に相当します。
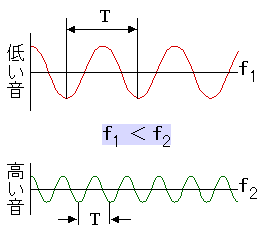
図2-2
位相
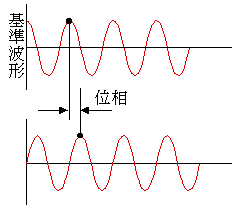
図2-3