6.畳込み積分
次章の窓関数を説明する前に、その基礎となる畳み込み積分と、その性質を見ておきましょう。前回の一般的なフーリエ変換、逆変換を参考にしてください。なお、同じ様な内容の繰り返しになっていることを理解してください。
6.1 畳込み積分
2つの時間関数 f1 (t)、f2 (t) が与えられているとき
|
(式6-1) |
で定義される関数 f (t) を f1 (t) と f2 (t) の畳み込み積分(合積:Convolution)と言います。式 6-1 を記号的に次式 6-2 のように表します。また、ここでは交換の法則が成り立ちます。
|
(式6-2) |
畳み込み積分のフーリエ変換は:
|
(式6-3) |
積分の順序を入れ替えて:
|
(式6-4) |
ここで、大括弧( )内の積分を考えてみます。f1 (t) ←→ F1 (ω)、f2 (t) ←→ F2 (ω) とし、t - τ = z と置くと、t = z + τ、dt = dz より;
|
(式6-5) |
よって;
|
(式6-6) |
すなわち時間領域の2つの関数 f1 (t)、f2 (t) の畳み込み積分はそれぞれの関数のフーリエ変換 F1 (ω)、F2 (ω) の積(周波数領域)になります。また、同様に f1 (t)、f2 (t) の積はそれぞれのフーリエ変換の F1 (ω)、F2 (ω) の周波数領域の畳み込み積分になります。フーリエ変換、逆変換を←→で表すと上記は次式 6-7 で表すことができます。
| (式6-7) |
6.2 移動平均と畳み込み積分
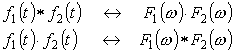
6-1 項の内容をサンプル値列で考えてみましょう。
サンプル値列 f (n) のある点を中心に、時間幅 b の間にあるデータの平均を求め、その平均値をある点の値とします。ある点を次々と次点に移動して同様に平均を取った新しい数値系列 fb (n) を考えます。このような方法を移動平均と言います。
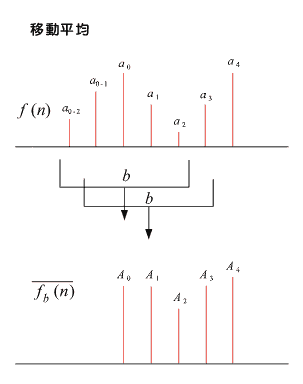
図6-1 |
例としてある点 a0 を中心に ±2 点の計 5 点をとり、その移動平均の様子を図 6-1 に示します。新しくできたデータ列 A0、A1・・・・・は;
|
(式6-8) |
上式はまとめて次のように表せます。
|
(式6-9) |
次に、図 6-2 のような幅 b、高さ 1/b、面積 = 1 の方形波 w (t) を考えてみます。
|
(式6-10) |
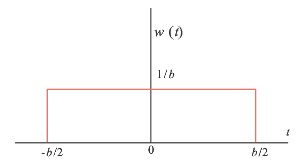
図6-2 |
式 6-10 を τ だけずらした場合を考えると;
|
(式6-11) |
これを式 6-9 の 1/b に代入すると、移動平均は;
|
(式6-12) |
と表され、畳み込み積分の式となります。
6.3 窓関数の概念
先の図 6-1 を考えてみると、これは同図 6-2 のような窓があり、それ以外は何も見えない、すなわち、窓から見えるもの全部を平均して窓の中心の値としながら、ちょうど列車の窓のように次々と移動していく様子にたとえられます。この様にデータの並びをみるという意味からこの W (t) を窓関数といいます。
また、図 6-2 の窓は平面ガラスのようにデータにひずみがなく、一様に平均化されています。このような窓をレクタンギュラウィンドウと呼びます。他に、ハニングウィンドウや、フラットトップウィンドウ等の窓関数がありますが、これらはいずれもデータに重み付け(weight)を持たせて平均化を行っています。図
6-2 のレクタンギュラウィンドウの窓関数 W (t) のフーリエ変換は:
|
(式6-13) |
この関数は次図 6-3 のようになり、FFT アナライザーでは b=T にとっていることになります。
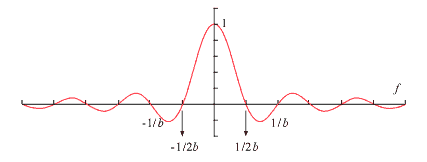
図6-3 |
6.4 スペクトルウィンドウ
次に周波数領域の移動平均を考えます。ある波形のスペクトルを G (f) とし、これに周波数関数 W (f) を乗じながら移動平均をとっていくと先の式 6-12 と同様にして、次式 6-14 が導かれます。
|
(式6-14) |
この式の中の W (f) をスペクトルウィンドウといいます。
平均化を行なうことにより元波形の持つパワーを変えないこと、ある点での平均を求めるときは左右対称性を保つ必要があります。
次に、 W (f) の例を考えてみましょう。
(a) 長方形パルス
図 6-2 と同じものを周波数領域で考えると、これは W (f) をある周波数域で切り取り、一定の重み付けで W (f) の移動平均を取ることの意味になります。
|
(式6-15) |
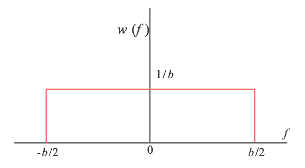
図6-4 |
この式の分散を求めます。分散 σ2 は標準偏差の2乗で次式として表されます。
|
(式6-16) |
(b) 長方形ウィンドウ
長方形ウィンドウは次式で表されます。
|
(式6-17) |
この関数の形は図 6-3 と同様な形になり、中心では大きく、中心から離れると重み付けが小さくなります。
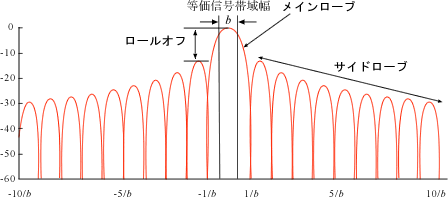
(a)の長方形パルスも(b)の長方形ウィンドウもある幅の間の周波数成分を通すと言う意味で帯域フィルター(バンドパスフィルター: Band Pass Filter)の作用をします。長方形パルスの場合は、バンド幅 b(-b/2 〜 b/2)ははっきりしていますが、この長方形ウィンドウではどこまでが帯域フィルターのバンド幅か明確ではありません。そこで、 1つの方法として、それぞれのウィンドウ関数の分散を計算し、それと等しい分散を持つ長方形パルスの幅を持って、そのウィンドウのバンド幅(等価信号帯域幅といいます)とすることが考えられます。
長方形ウィンドウの分散を計算すると;
|
(式6-18) |
長方形パルスと等しい分散を持つ長方形ウィンドウの幅は、式 6-16 と式 6-18 より;
|
(式6-19) |
この様子を次図 6-5 の中に青線で示しています。
一般的に表すと;
|
(式6-20) |
となります。
また、式 6-17 を逆フーリエ変換した関数 W (f) を求めると;
|
(式6-21) |
これは図 6-2 で u = b/2 と置き換えた同様な長方形となります。式 6-17、6-21 を図 6-5、6-6 に示します。
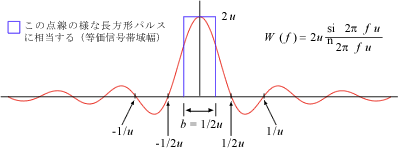
図6-5 |
|
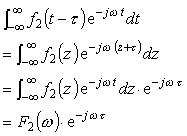
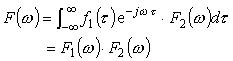
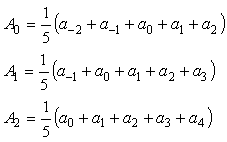
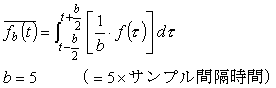
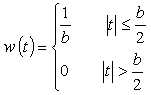
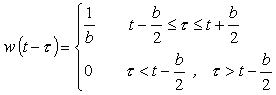
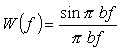
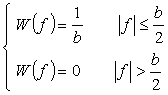
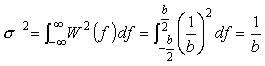
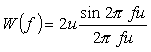
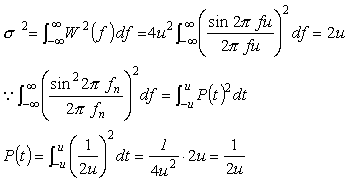
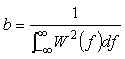
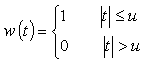
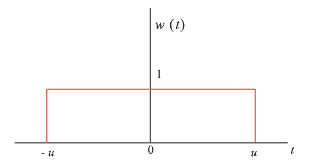 図6-6
図6-6