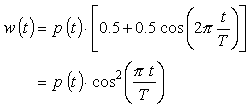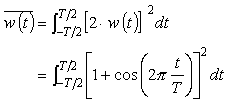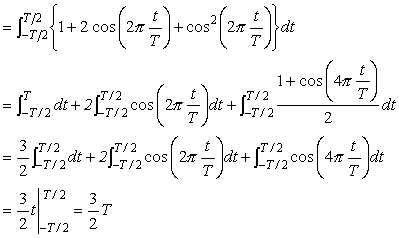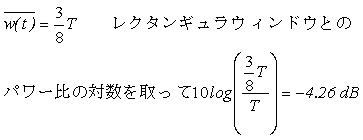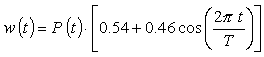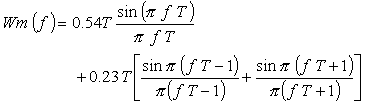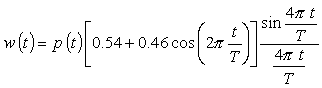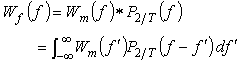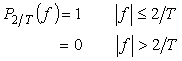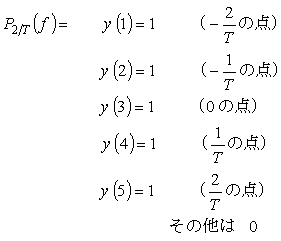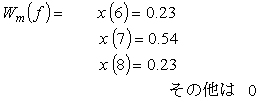7.2 ハニングウインドウ(Hanning window)
FFT と言えばハニングウインドウといわれるほど良く使用されている実用的な窓関数です。
ハニングウインドウは次式で与えられます:
|
|
(式7-8) |
このフーリエ変換は;
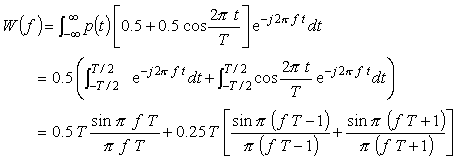
(式7-9)
W (f) を DFT で表すと;
n / T (n = 0)のとき: 0.5
n = ±1 のとき:0.25
n = その他のとき: 0
パワー減衰率 = -4.26 dB
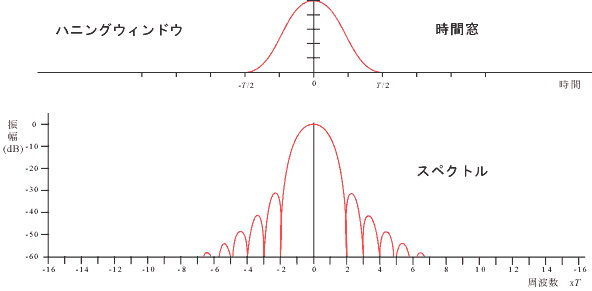
式 7-9を図 7-10 に示します。図を見ていただくとお分かりいただけるように、スペクトルの主部がレクタンギュラウィンドウに比べ約2倍に広がりますが、副部では急速に減衰しています。
|
図7-10 |
ハニングウインドウは、高周波側の漏れが少ないため方形波窓より f0 の分離がより明確になるという特長を有しています。先のレクタンギュラウィンドウと同じ周波数分解能を得るには、窓の長さを 2倍の 2T に取らなくてはなならいことになります。FFT アナライザーで窓の長さを 2T に取るには、周波数レンジを下げるか、あるいはデータ長変更機能で対応することになります。
レクタンギュラウィンドウでは、切り取られた波形には振幅のひずみはありませんが、ハニングウインドウを掛けると、波形の振幅がゆがめられるため、そのパワーが減少します。
f0 の振幅が直読にできるよう 1 / 0.5 T 倍した、正規化後のパワーは;
|
|
(式7-10) |
b = 3/2 T になり、ハニングウインドウはレクタンギュラウインドウのフィルター幅に比べ、3/2 倍広いことになります。
正規化前の w (t) のパワーは;
|
|
(式7-11) |
となり、レクタンギュラウィンドウに比べ -4.26 dB パワーが減少します。この値をパワー減少率としてそれぞれのウインドウ式の後に記します。
スペクトルのオーバーオール値を求めるとき、これではレクタンギュラウインドウに比べ 3/2 倍大きい値になってしまうため、FFT アナライザーでは、オーバオールの計算時にこの分のウィンドウ補正を行い、表示しています。
7.3 ハミングウインドウ(Hamming window)
ハニングウインドウ主部に隣接する副部のスペクトルを更に小さくするためのウインドウがハミングウインドウです。ハミングウィンドウでは、副部が主部の 1/100 以下になります。
ハミングウインドウとそのスペクトルは次式で与えられます:
|
|
(式7-12) |
|
|
(式7-13) |
Wm (f) の DFT では:
n / T の(n = 0)の時: 0.54
n = ±1 の時: 0.23
n = その他の時: 0
パワー減少率:−4.0 dB
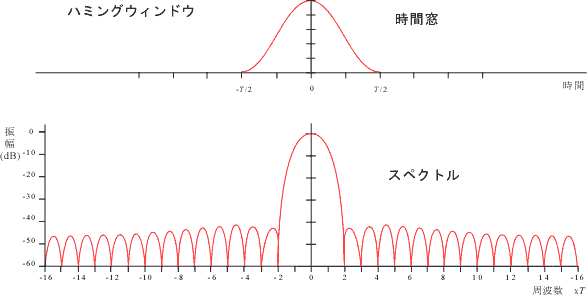
式 7-13 を図 7-11 に示します。
|
図7-11 |
7.4 フラットトップウインドウ(flat-top window)
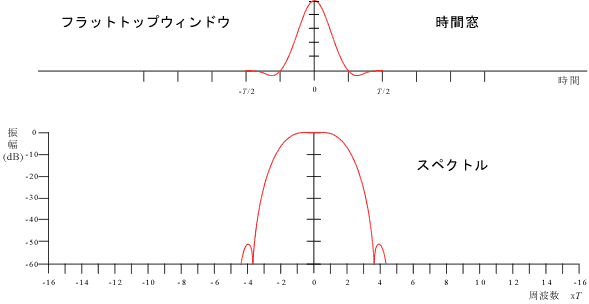
レクタンギュラやハニング、ハミングウインドウのスペクトルは頂上部が平ではありません。そのため、cos 波、sin 波、方形パルス波などの線スペクトルを持つ波形では、DFT すると、時間窓長が波の周期のちょうど整数倍にならない限り各周波数に相当するスペクトルの大きさは実際よりも小さい値で表現されてしまいます。そこで時間窓長が基本周期の整数倍でなくても周波数成分の大きさにあまり変化を生じない時間窓として、フラットトップウィンドウが考え出されました。フラットトップウィンドウは、ハミングウインドウに -2 / T 〜 +2 /T までフラットなスペクトルを持つ波形 sin (4π t / T) /4π t / T を掛けたもので、このスペクトルは図 7-12 の様に頂上部が平らになります。
フラットトップウィンドウは、この解説の参考書として利用させていただいている「デジタル信号処理入門」の著者城戸健一氏が考案された窓関数です。
フラットトップウィンドウを式で表すと:
|
|
(式7-14) |
また、このフーリエ変換は、式 7-13 と式 7-16 の畳み込み積分として次式で与えられます。
|
|
(式7-15) |
ここで:
|
|
(式7-16) |
パワー減少率:-7.0 dB
式 7-14、式 7-15 を図 7-12 に示します。
|
図7-12 |
7.5 フラットトップウィンドウの近似計算
DFT での表現は簡単ではありませんので、ここでは、畳み込み積分の練習として、ハニングウインドウの主部および式 7-13 と式 7-16 の離散的スペクトル値を採用し、式 7-15 の畳み込み積分をしてみましょう。
|
|
(式7-17) |
|
|
(式7-18) |
畳み込み積分は、先に述べたように移動平均ですから、Wm (f) が x (1) 〜 x (12) の駅で、P2/T (f) が先頭から y (1) 〜 y (5) の列車とし、列車が駅を通過するように考えて Wf (n) を計算してみます。この計算の様子を表1に、また求めた Wf (f) の簡略図を図7-13に示します。
|
X(1) |
X(2) |
X(3) |
X(4) |
X(5) |
X(6) |
X(7) |
X(8) |
X(9) |
X(10) |
X(11) |
X(12) |
||
|
0 |
0 |
0 |
0 |
0 |
0.23 |
0.54 |
0.23 |
0 |
0 |
0 |
0 |
||
|
W(1) |
0 |
1 y5 |
1 y4 |
1 y3 |
1 y2 |
1 y1 |
|
|
|
|
|
|
|
|
W(2) |
0.23 |
|
1 |
1 |
1 |
1 |
1 y1 |
|
|
|
|
|
|
|
W(3) |
0.77 |
|
|
1 |
1 |
1 |
1 |
1 y1 |
|
|
|
|
|
|
W(4) |
1 |
|
|
|
1 |
1 |
1 |
1 |
1 y1 |
|
|
|
|
|
W(5) |
1 |
|
|
|
|
1 |
1 |
1 |
1 |
1 y1 |
|
|
|
|
W(6) |
1 |
|
|
|
|
|
1 |
1 |
1 |
1 |
1 y1 |
|
|
|
W(7) |
0.77 |
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 y1 |
|
|
W(8) |
0.23 |
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 y1 |
|
W(9) |
0 |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 y2 |
表1 フラットトップウィンドウの近似計算(畳み込み積分)
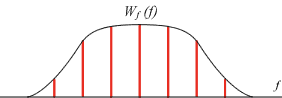
図7-13 表1より求めたフラットトップウィンドウの DFT |
例えば、Wf (4)、Wf (5) を求める式を、0 との掛け算分を省略して示すと;
W (4) = x (8) y (1) + x (7) y (2) + x (6) y (3) + x (5) y (4) + x (4) y (5)
W (5) = x (9) y (1) + x (8) y (2) + x (7) y (3) + x (6) y (4) + x (5) y (5)
となります。
フラットトップウインドウは接近した線スペクトルを分離するには向きませんが、その線スペクトルの振幅を正しく求めるには非常に有効な窓関数です。
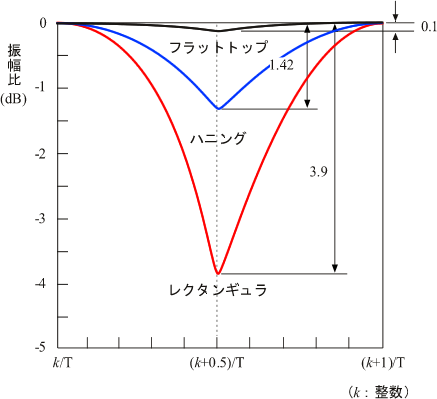
図 7-14 はそれぞれのウィンドウの主部の片側を重ねて表示したもので、ウインドウ(フィルター)による違いが良くわかると思います。
|
図7-14 ウィンドウによるフィルターの形のレベル確度 |
一般的に、周期性を持った信号やランダム信号の分析で、周波数を重視するときにはハニングウインドウを、振幅を重視するときにはフラットトップウインドウを使用し、打撃試験で伝達関数を測定するときはレクタンギュラウインドウを使うといわれていますが、このことは、それぞれのウインドウの特徴からきていることがお分かりいただけると思います。また、時間長 T を長く取れば取るほど、 リーケッジエラーのパワーが小さくなり、影響は軽減されます。なお、その他にもいろいろな窓関数が提案されていますが、ここでは割愛させていただきます。
これまでに取り上げたウインドウの特長を表2に示しますので参考としてください。
| ウィンドウ名 | -3dBの帯域幅 |
最大サイドロープ (dB) |
ロールオフ (サイドロープの減衰特性) dB/OCT |
等価信号帯域幅 (b) |
パワー低下率 (dB) |
レベル確度
(1.5/Tの点の減衰量) (dB) |
|---|---|---|---|---|---|---|
| レクタンギュラ | 0.89/T | 13 | -6 | 1.00/T | 0 | -3.9 |
| ハニング | 1.44/T | -32 | -18 | 1.50/T | 4.26 | -1.42 |
| ハミング | 1.30/T | -43 | -6 | 1.36/T | 4.01 | |
| フラットトップ | 3.67/T | 7.0 | -0.1 |
表2 ウィンドウの特徴