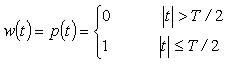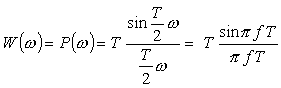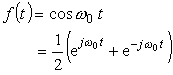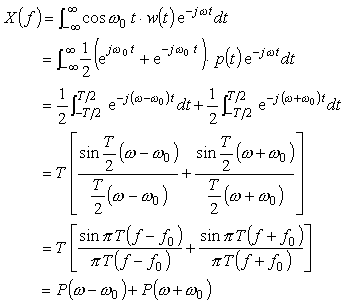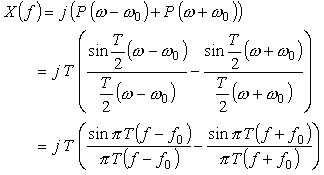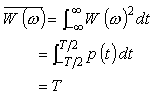7.1 レクタンギュラウィンドウ(rectangular window)
|
|
(式7-2) |
で定義される方形パルス p (t) をレクタンギュラウィンドウ(方形波窓関数)といいます。これは単に時間長 T で切り取ったそのままのデータと同じです。このフーリエ変換は前項より;
|
|
(式7-3) |
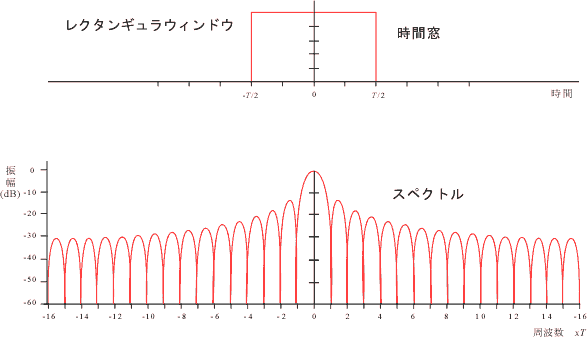
P (ω) を図で表すと次図 7-5 のようになります。図の上側は時間窓の形、下側はスペクトルの絶対値の対数表示で周波数軸の目盛りの単位は時間窓長の逆数となります。
|
図7-5 |
なお、図 7-5 は f0 の時1になるよう正規化して表示しています。これにより、f0 の時の振幅が直読になります。以後の図示は全て正規化して表示していますので注意ください。
◆ f (t) = cos ω0 t への適応
f (t) として cos ω0 t を考えて見ます。cos 2π f0 t・w (t) は周波数 f0 の cos 波形が w (t) 倍に振幅が変えられた(振幅変調された)波形になります。
方形波窓で切り取った波形のフーリエ変換は;
|
|
(式7-4) |
より;
|
|
(式7-5) |
◆ f (t) = sin ω0 t への適応
cos 波形の代わりに sin 波形を考えると同様に:
|
|
(式7-6) |
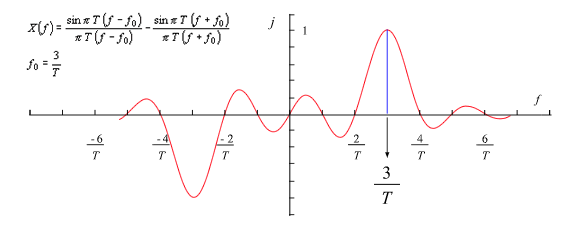
式 7-5、式 7-6 の第1項と第2項は、 P (ω) の中心 0 を±f0 に移動させた波形となり、また、式 7-5 はその和を、式 7-6 はその差を取ったものとなります。f0 = 3 /T に取ったときの式 7-6 の波形を図 7-6 に示します。さて、図 7-6 での DFT の値は、周波数 1/T の高調波の点を取るので、その点の値を見ると:
f0(n = 0)のとき:W (f0) =1
f0 ± n /T(n = 1、2、.....)のとき:W (f) = 0
となり、すなわち sin ω0 t は周波数 f0 であることを良く表わしています。
これは先の図 7-1 のように sin 波形の周期に一致して切り取られているため、始端と終端が連続になっているからです。
|
図7-6 |
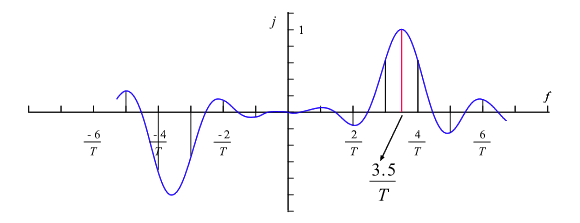
次に周期に一致しないで切り取られる f1 = 3.5 / T の場合を考えると図 7-7 で縦線で示したように;
f1 (n = 0)のとき:≠ 0
f1 ± n / T (n = 1, 2, 3, ..... )のとき:≠ 0
と、f1 ± n / T で値を持ちます。DFT では f1 の点を持たないので図 7-5 と違い、f0 の高調波スペクトルを持つことになります。これは切り取りの始点と終点が不連続であることに起因する誤差で、 リーケッジエラー(leakage error)と言われます。 f0 の他に fn のスペクトルを持つ信号を分析する場合は、 fn の成分が小さすぎると f0 のリーケッジエラーに埋もれてしまうこととなります。(図 8-3 のレクタンギュラウィンドウを参照ください。)
|
図7-7 |
図 7-8 に図 7-6 と 7-7 を重ねて書いたものを示します。この図からわかるように f0 = 3 / T の時の 3.5 / T の点のY軸の値Cと、f1 = 3.5 / T の時の 3 / T の値 B は同じになります。図 7-7 の B 以外のスペクトルも同様になることを考えると、f1 = 3.5 / T の波形がバンドパスフィルターである P (ω)(図 7-5 を f0 にシフトした形)を通過したものと考えることができます。
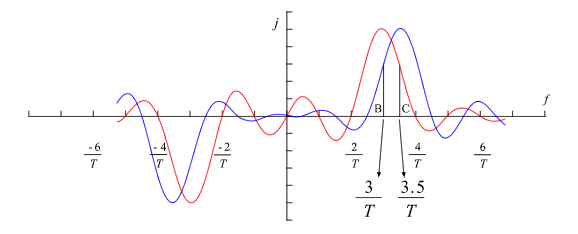
図7-8
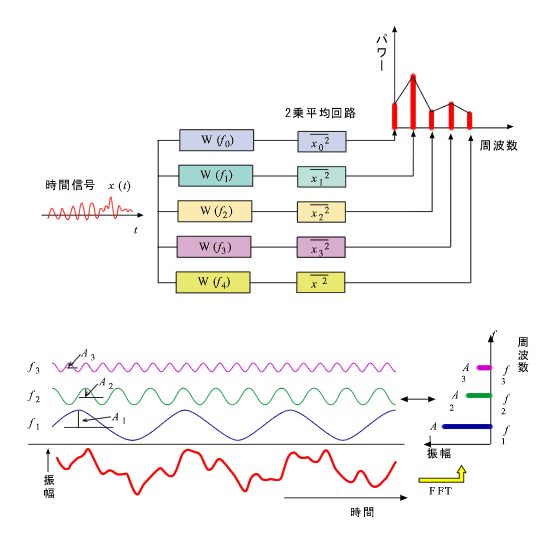
上述のことから、FFT アナライザーの概念として、f0 を基本周波数とする n 次高調波のスペクトルを求める DFT は、バンドパスフィルターの形が W (f) の形を持ち、このバンドパスフィルターの中心周波数を f0 だけずらしながら n 個ならんだ多数のバンドパスフィルターに置き換えて考えることができます。この様子を図 7-9 に示します。
|
図7-9 |
レクタンギュラウィンドウは f (t) が打撃波形のように始点と終点がゼロとなる信号では合理的な窓となりますが、連続信号の場合には リーケッジエラーにより周波数分離性が良くありません。
これまで見てきたように窓関数によるパワースペクトルの変化は、窓関数のフーリエ変換の特性に依存するので W (f) の性質を調べれば良いことになります。
このパワー平均はパーシバルの定理より周波数領域、時間領域どちらも同じなので:
|
|
(式7-7) |
正規化して対数で表すと 0dB となり、またこの逆数は分散 b の式に一いたします。これは同じパワーを持つと仮定したときの帯域幅を表し、ウィンドウの特徴を表すパラメーターの1つとなります。