8.FFTアナライザーによる窓関数解析例
窓関数による違いをFFTアナライザーでの解析例としてここに揚げておきますので、参考としてください。FFTアナライザーで信号を解析する際、求めたい値がスペクトルの周波数なのかあるいは振幅なのかによって窓関数を使い分ける必要があることや、 リーケッジエラーを低減し精度良く解析するためにはサンプリング点数を適切に設定しなければならないことがここでの例からお分かりいただけると思います。
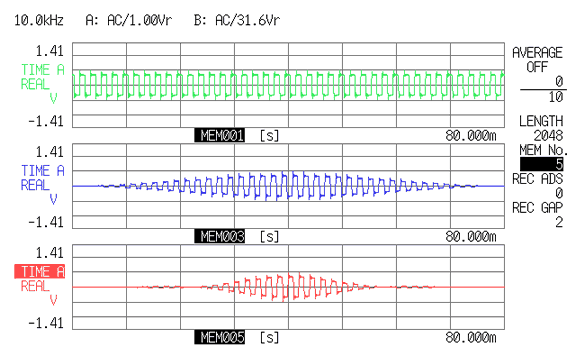
図8-1
上図 8-1 は、方形波形をある時間長で切り取り、窓関数を適用した結果表示です。上から、レクタンギュラウィンドウ、ハニングウィンドウ、フラットトップウィンドウが同じ波形に適用されています。
|
図8-2 |
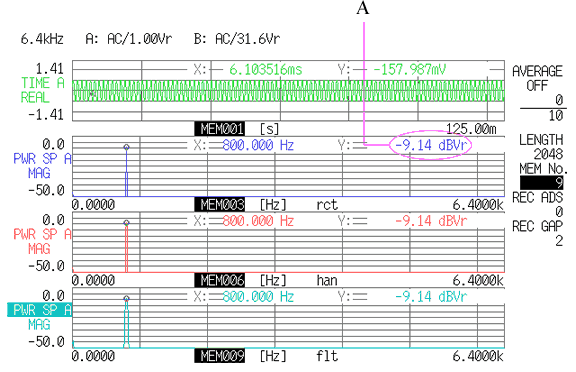
上図 8-2 の一番上は、800 Hz の正弦波形を 6.4 kHz レンジで、2048 点サンプリングした時間軸波形で、2番目以降が、その波形にレクタンギュラ、ハニング、フラットトップの各ウィンドウを適用した際のスペクトル波形です。時間長 T = 125 ms は、800 Hz の 100 周期分(0.125 ×800 = 100)として切り取ることができるため、各スペクトルの 800 Hz にピークが現れています。
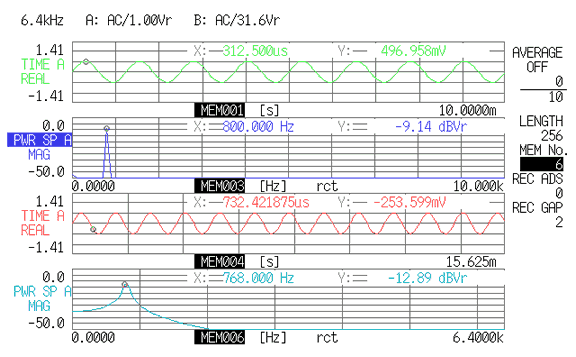
図8-3
上図 8-3 は、サンプリング点数を 256 点(時間長 T = 15.625 ms)にとり、レクタンギュラウィンドウを適用して FFT 分析した結果表示です。上から、10 kHz レンジでの時間軸波形、次がその FFT、3番目が 6.4 kHz レンジでの時間軸波形、4番目がその FFT です。10 kHz レンジでは 800 Hz に同期して切り取りが行われているため 800 Hz にピークが表れていますが、6.4 kHz レンジではうまく同期して切り取りができず不連続点による リーケッジエラーが発生するため、スペクトルの漏れが波形の裾の広がりとして現れています。また、分解能 = 6400/100 = 64 Hz のため、800 Hz という周波数は無く、768 Hz(= 64 Hz×120 line)と 832 Hz(= 64 Hz×121 line)に分かれてスペクトルのピークが現れ、かつ 768 Hz の Y 軸の値は 10 kHz レンジに比べて小さくなっています。その減衰分は、先の図 7-14 でのウィンドウ減衰となります。
|
図8-4 |
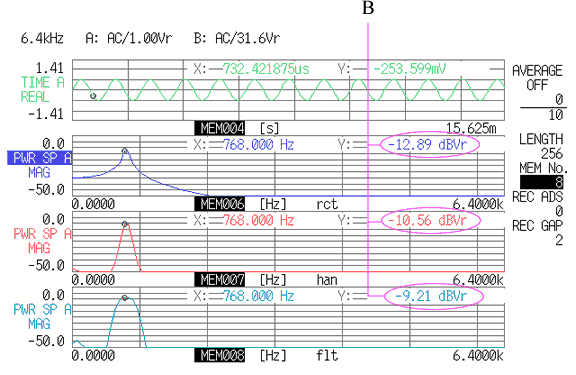
上図 8-4 は、6.8 kHz レンジ、サンプリング点数 256 点で、窓関数を変えて FFT 分析した結果表示です。一番上が時間軸波形で、2番目以降がレクタンギュラ、ハニング、フラットトップの各ウィンドウを適用したスペクトル波形を示しています。各スペクトル波形の 800 Hz の振幅値(図中の B の値)を見ると、フラットトップウィンドウを適用した場合の値が最もよくその振幅を現しています。しかし、このフラットトップウィンドウでは、ピーク周波数の幅が広がっているため、ピーク周波数が 800 Hz とは判断しづらいところです。図8-2の A とここでの B を比較してみてください。