1. Introduction
Vibration is unavoidable phenomenon when the machine is working. Vibration is not only unpleasant, but also cause of fault, and leads to breakdown of the machine. It is important to thoroughly consider vibration in advance when designing machine, and take measures not to generate or reduce vibration since it take time and cost to take measures once having vibration. The measures of vibration are indispensable for buildings and bridge.
There are 4 major measures:
1. Interrupt the source of vibration
2. Design the structure that does not vibrate easily
3. Add damping
4. Counteract vibration
This article focuses on “damping” and explains how to obtain the coefficients such as damping ratio, logarithmic decrement and Q factor and the effect of the coefficients in the phenomenon of vibration.
2. Coefficients that represent damping characteristics
Coefficients that represent damping characteristics such as damping vibration and damping materials include damping ratio (damping factor), logarithmic decrement, loss factor, and Q factor. The definition and physical meaning of each coefficient will be explained later, and then we will explain how to obtain these coefficients first.
2-1 Logarithmic decrement δ
In general, the amplitude of damped free vibration waveform exponentially attenuates as shown in Figure 1. Taking the logarithm of the adjacent amplitude ratio, it is always a constant value. The natural logarithm of this the adjacent amplitude ratio is called the logarithmic decrement, which is widely used as a simple coefficient that represents damping characteristics. The damping ratio, loss factor which are characteristic value in terms of physics are calculated by the logarithmic decrement.
Fig.1 The logarithmic decrement |
Assuming that the n th amplitude at time tn is an, and n + 1, ... n + m th amplitude is an + 1, ... an + m, the logarithmic decrement δ is defined as the following equation.
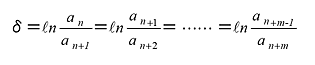 |
(1) |
If the accuracy is not enough in one cycle, calculate with m cycle.
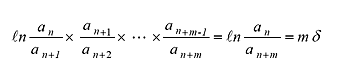 |
(2) |
then
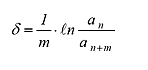 |
(3) |
The damping ratio ζ and loss factor η are calculated by δ.
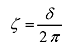 |
(4) |
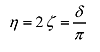 |
(5) |
2-2 Calculation of the logarithmic decrement and damping ratio by Hilbert transformation
The logarithmic decrement and damping ratio are obtained by the Hilbert transformation function of FFT Analyzer. The attenuation waveform of Fig. 1 is taken into the FFT analyzer as time-axis waveform, converted to an envelope curve of amplitude by performing Hilbert transform, and the Y axis is displayed as dB, a straight line with a downward slope as shown in Fig. 2 is obtained.
Fig.2 The calculation by Hilbert transformation |
Using the Δ cursor, ΔX and ΔY between the two points in this straight line are obtained, and you can calculate the logarithmic decrement δ and damping ratio ζ using the following equation. If the vibration frequency is fd,
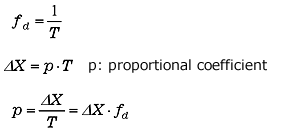 |
|
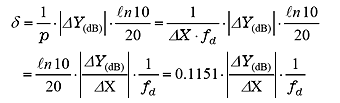 |
(6) |
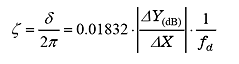 |
(7) |
(fd, is obtained from frequency spectrum. The damping ratio ζ is able to be automatically calculated by some Analyzers.)
2-3 Calculation of damping ratio by half band width method
To be mentioned later, the vibration system shows resonance characteristics when the damping ratio ζ is small. The damping ratio, loss factor, and Q value can be calculated from the frequency/ amplitude characteristics near the resonance frequency.
Fig.3 Half band width method |
In the frequency/ amplitude characteristics shown in Fig. 3, using the peak frequency f0 of the amplitude and the frequency width Δf at 3 dB below from the peak value, the Q value, loss factor η, and damping ratio ζ are obtained by the following equations.
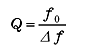 |
(8) |
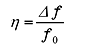 |
(9) |
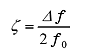 |
(10) |
Since -3 dB in amplitude, that is![]() , is equivalent to 1/2 of energy, this calculation method is called as half band width method.
, is equivalent to 1/2 of energy, this calculation method is called as half band width method.
Notes The damping ratio can be obtained by the half band width method only when the value of ζ is small (at most 0.1 or less). In other words, when the frequency/ amplitude characteristics show a clear single peak characteristic as in Fig. 3, the damping ratio and damping coefficient can be obtained by the half band width method. (Please refer to (Supplement) “Calculation derivation of half band width method”.) |
The damping ratio and logarithmic decrement are used as evaluation indexes and design parameters for vibration characteristics of machines and structures. Loss factor is used as evaluation index for the damping materials. Q value is used for the evaluation of electrical and mechanical resonance characteristics. When obtaining the damping coefficient of the material with large loss factor, the damping rate method obtained from the attenuation per second or impedance method are used. The performance measurement of damping material is explained in detail below.
“Damping materials and their performance” - Ono Sokki, Technical report
http://www.onosokki.co.jp/HP-WK/c_support/newreport/damp/damp_index.htm