4. Summary of relational expression
5. Conclusion
It is important for mechanical design to keep vibration within allowable level as vibration is unavoidable phenomenon during machine operation. Especially it is careful to pay attention to resonance since it may cause large vibration with even small external force. It is ideal not to have natural resonance frequency (natural frequency) and forced vibration frequency at the same time. However, realistically there is natural frequency within operational area, it is difficult problem for engineers to solve this phenomenon.
As explained in this article, resonance behavior varies greatly with damping. Therefore, it is reasonable to design to take appropriate damping to keep vibration within allowable level. Adding damping element like damper is often used to reduce vibration generated from machinery or structure. In that case, basic knowledge about damping which we explained is required. Although we explain simple model which has 1 freedom degree system and external force is sin-wave, actual machinery and structure have more complicated systems, external force is irregular waveform. It is not easy to analyze vibration as damping rate varies with amplitude or state. The basic theory of mechanical vibration is 1 freedom degree system model and most of vibration behavior will be explained by the knowledge we explained in this article. Hope this article will give a clue to do vibration analysis and to take measures for vibration.
We have briefly explained about the meaning of coefficients that represent damping characteristic, mainly damping rate. It would be greatly appreciated that this article is useful for the person who is not expert in vibration when taking countermeasures.
⟨Supplemental⟩ Calculation method of half band width method
Equation of the maximum amplitude (22) will be obtained by substituting equation of resonance frequency into equation of amplitude magnification (21).
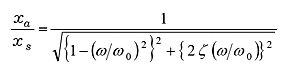 |
(21) |
Substituting equation of resonance frequency ![]() into
into ![]() of equation (21)
of equation (21)
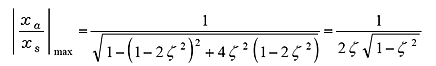 |
(22) |
Obtaining frequency with the maximum amplitude ![]() from equation (21) and (22).
from equation (21) and (22).
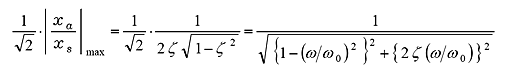 |
(28) |
Re-arranging;
(29) |
Solving this;
(30) |
|
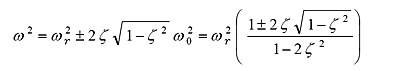 |
(31) |
When ζ ≪ 1, ζ 2 ≒ 0. Then;
(32) |
|
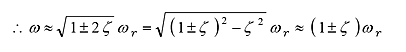 |
(33) |
If![]()
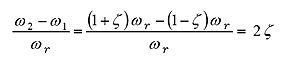 |
(34) |
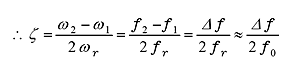 |
(35) |
As shown above, accurate calculation will be performed when ζ is 0.05 or less or up to the upmost 0.1 or less as the equation which obtains damping rate from half band width method is close to the equation when ζ ≪ 1 .
⟨Reference⟩ Damping rate for structure and machinery
The actual damping rate for structure and machinery are as follow:
| Steel frame building | 0.003 to 0.04 |
| Medium low storied building(10 floor or less) | 0.005 to 0.12 |
| Multistory building | 0.02 to 0.1 |
| Steel tower | 0.002 to 0.03 |
| Concrete tower | 0.01 to 0.02 |
| Highway bridge | 0.02 to 0.05 |
| Suspension bridge | 0.002 to 0.08 |
| Suspension for large size automobile | 0.1 to 0.3 |
| Suspension for small size automobile | 0.2 to 0.5 |
| Suspension for motorcycle | 0.35 to 0.45 |
⟨Reference materials⟩
“Control of vibration” written by Kohei Suzuki, Ohmsha (written in Japanese)
“Compendium of Automotive engineering 11”, Sankaido (written in Japanese)