24.Physical property of viscoelasticity materials
The polymer material exists in a state where the crystalline and non-crystalline are mixed while each molecular chain is entangled randomly, and temperature / frequency dependence depends on molecular viscoelasticity. The molecular chains of these materials have various modes of motion, and each mode releases energy at specific temperature and frequency. The damping performance becomes greatest in the transition state where this molecular motion becomes active. The local motion of the main chain of the material molecule in the glass state changes to the micro-brownian motion in the transition state, which gives the greatest loss. The temperature-frequency superposition , W.L.F. Equation(Williams, Landel, Ferry)is completed in this transition state. The important basic concept is that the same elastic modulus characteristics can be expressed for the frequency by switching the temperature and frequency (the temperature frequency superposition: Master Curve used) based on the temperature characteristics of the elastic modulus of the viscoelastic material shown in Fig. 1.
The temperature characteristics of viscoelasticity materials |
The complex elastic modulus (longitudinal, transverse elastic) of viscoelastic materials such as polymer and rubber used as damping materials expresses a functionality of temperature T and frequency f. It is known that when a certain temperature T0 is set as a reference temperature by taking the complex elastic modulus at vertical axis and the frequency at horizontal axis at temperature T1, and this is translated in the direction of the horizontal axis, it matches the complex elastic modulus at the reference temperature T0. It means that higher temperature corresponds to lower frequency (longer time), lower temperature corresponds to higher frequency (shorter time). The temperature- frequency superposition enables to convert temperature changes into frequency changes in this way. Since the damping characteristics (dynamic characteristics) of the damping material depend on both temperature and frequency, a three dimensional display is required to express the elastic modulus and loss factor for both parameters. Then, the temperature frequency superposition is effective. The temperature frequency superposition is very useful for viscoelastic materials (especially glass transition state). By replacing the change of temperature with frequency (reduced frequency), the dynamic characteristics of the damping material can be expressed in two dimensions. This means finding the temperature frequency superposition that satisfies both characteristic values of the elastic modulus and loss factor at the same time. In other words, the law that if the temperature changes by T, it is equivalent to changing the frequency by f is found in such a way that it can be applied to both elastic modulus and loss factor at the same time in a wide temperature and frequency range. The temperature frequency superposition has been researched in the field of the rheology of polymer materials, and the most famous is the WLF equation that shows the temperature dependence of the shift factor αT obtained for many polymer materials.
2. WLF equation
The relationship between the shift factor αT and the temperature T has been analyzed for various viscoelastic materials, and it is arranged as the Williams-Landel-Ferry (WLF) equation as follows:
Equation 1 |
■ Derivation of WLF equation
When an amorphous polymer (not crystalline) exhibits a relaxation phenomenon, the space where the segment can move, that is, the free volume, is considered to dominate the mobility and internal viscosity of the segment. From doolittles’s viscosity equation based on the free volume concept,
Equation 2 |
taking its natural logarithm,
Equation 3 |
The above represents the relationship between elastic modulus η and free volume in terms of molecular theory. f is free volume rate, B is almost 1. Then, doolittle equation is as follow:
Equation 4 |
Here’s comparison, the viscosity ηT at arbitrary temperature T with viscosity ηTg at glass transition point Tg. The elastic modulus of these temperatures is
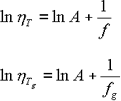 |
Equation 5 |
f 、fg is the free volume rate at T と Tg. When the temperature dependency of relaxation time T is also considered to be doolittle type, the following equation is true:
Equation 6 |
The next question is how to express the temperature dependency of the free volume fraction f. In terms of the relationship between specific volume and temperature, the thermal expansion coefficient in the glass state is not much different from the crystal one, but increases rapidly when Tg is exceeded. If the temperature dependency of f is almost the same as mentioned above,
Equation 7 |
αf is the coefficient of the difference of free volume fraction above Tg
Equation 8 |
converting to common logarithm,
Equation 9 |
The above equation has the same formula as the previous WLF equation (Equation 1). By comparing the coefficient parts, it can be seen that the coefficients C1 and C2 in WLF equation are as follows:
WLF equation |
(Equation 1) |
Equation 10 |
|
Equation 11 |
|
C1 、C2 : Constant |
The reduced frequency fr is expressed as the product of shift factor and measurement frequency.
Equation 12 |
The relationship between shift factor (αT : transfer coefficient) and WLF equation is shown in Figure 2, the relationship between temperature and shift factor by setting C1= 17.44、C2 = 51.6 in WLF equation, Tg as parameter is shown in Figure 3.
Fig.2 Comparison of Master curves |
Fig3. Shift parameter of WLF equation |