22.Window function for the measurement of loss factor
The frequency response function will be transformed when measuring loss factor by window function. The following figures show the lower limit for the measurement of loss factor when measuring by each window functions.
|
The above figures find it as follow:
The flat-top window function is not suitable for the measurement of loss factor.
The square window function is the best except the signal is input to the worst case resolution and the center position of the resolution.
It has been common the hanning window function is used as the window function when the signal is asynchronous. However, the square window function enables to measure the lowest of loss factor with accuracy only when measuring loss factor (in case of obtaining η greater than -13 dB from the peak).The taper window function is used when lowering coherence by the rectangular window.
The closer the resonance point is to the left side of the FFT screen, the greater the influence of the window function. For example, the measuring lower limit for the 10th line of FFT is η = 0. 15 without zooming but using hanning window.
The fact that the peak of waveform for the frequency response function is on the left side of the screen means that the low-frequency resonance / anti-resonance are measured by high frequency. Shifting the peak to the right means (1) lowering the frequency range, (2) performing zooming frequencies, therefore, it finds necessary to perform zooming analysis.
Another benefit of zoom analysis is that the protruding transformation of impulse response is reduced as the time frame is longer. Furthermore, as the frequency resolution is increased, the reduction in error can be expected. A similar effect can be expected by increasing the number of FFT points. There is the device which calculates the spectrum of 25,600 lines with 65,536 points of FFT recently. When the loss factor is large to some extent, it is easy to be used by the one without zooming analysis.
23. How to calculate Young's modulus
The calculation for Young’s modulus obtained from a measurement of pure material and the calculation which loss factor, Young’s modulus for single damping material is obtained from loss factor, Young’s modulus measured by the compound type (dual, three layers) with RKU (Ross, Kerwin, Unger) equation are shown as follow:
■ Pure material
The resonance frequency fn (Hz), half value width δ fn (Hz), length of specimen beam ![]() (m), thickness of specimen beam h (m), mean density of specimen beam ρ (kg/m3):
(m), thickness of specimen beam h (m), mean density of specimen beam ρ (kg/m3):
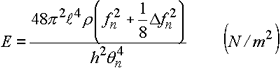 |
When the damping value is small, 1/8 δ fn2 is ignored
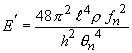
|
and loss factor η is
When using the cantilever and the central exciting method with anti-resonance:
| degree n |
θn | θn4 |
|---|---|---|
| 1 | 1.87510 | 12.36 |
| 2 | 4.69409 | 485.5 |
| 3 | 7.85476 | 3806.6 |
| 4 | 10.99554 | 14617.3 |
| 5 | 14.13717 | 39943.8 |
| 6 | 17.27876 | 89135.4 |
| 7 | 20.42035 | 173881.2 |
| 8 | 23.56194 | 308208.2 |
As follows + π |
||
In case of the cantilever method, input the full length except gripping margin as In case of the central exciting method with anti-resonance, input the half length of |
||
When using the central exciting method with resonance, obtain the resonance frequency and use the following value for θ n.
| degree n | θn | θn4 |
|---|---|---|
| 1 | 4.73004 | 500.56 |
| 2 | 10.99561 | 14617.6 |
| 3 | 17.27876 | 89135.4 |
| 4 | 23.56194 | 308208.2 |
| 5 | 29.84513 | 793403.1 |
| 6 | 36.12831 | 1703690.0 |
| 7 | 42.41150 | 3235448.8 |
| 8 | 48.69468 | 5622456.0 |
As follows + π |
||
Two points hanging method with free ends
| degree n | θn | θn4 |
|---|---|---|
| 1 | 4.73004 | 500.56 |
| 2 | 7.85320 | 3803.5 |
| 3 | 10.99561 | 14617.6 |
| 4 | 14.13717 | 33943.8 |
| 5 | 17.27876 | 89135.4 |
| 6 | 20.42035 | 173881.2 |
| 7 | 23.56194 | 308208.2 |
As follows + π |
||
At higher degree, the difference between θn+1 and θn is almost equal to π
The above calculation which degree factor θn and density ρ are eliminated is useful if you’re not sure about degree.
■ The laminated composite sheets
| Loss factor of composite plate: η c
Resonance frequency:fc[Hz] Free length: Loss factor of base material: η1 = 0 Resonance frequency:fi[Hz] Thickness:d1[m] density: ρ 1[kg/m3] Young’s modulus: E1[N/m2] Loss factor of single damping material: η 2 Thickness:d2[m] density: ρ 2[kg/m3] Young’s modulus: E2 [N/m2] |
|
The loss factor and Young's modulus of a single damping material can be calculated by the following calculation from the data of the base material itself and the composite specimen when inputting Young’s modulus rate E2 / E1 = M, thickness rate d2 / d1 = T, density rate ρ2 / ρ 1 = d.
|
in the above
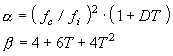 |
This is valid only whenα ≧ 1.1.
■ The composite sheets with base between the damping materials
| Loss factor of composite plate: η c
Resonance frequency:fc[Hz] Free length: Loss factor of base material: η1 = 0 Resonance frequency:fi[Hz] Thickness:d1[m] density: ρ 1[kg/m3] Young’s modulus:E1[N/m2] Loss factor of single damping material: η 2 Thickness:d2[m] density: ρ 2[kg/m3] Young’s modulus: E2 [N/m2] |
|
The loss factor and Young's modulus of a single damping material can be calculated by the following calculation when inputting thickness rate d2 / d1 = T, density rate ρ2 / ρ1 = d.
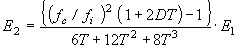 |
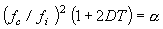
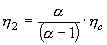 |
This is valid only when
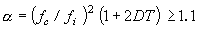 |
■ The shear modulus and loss factor for the composite sheets with the damping material between base and constrained layer
| Loss factor of composite plate: η c
Resonance frequency:fc[Hz] Free length: Loss factor of base material: η1 = 0 Resonance frequency:fi[Hz] Thickness: d1[m] density: ρ 1[kg/m3] Young’s modulus:E1[N/m2] Loss factor of single damping material: η 2 Thickness:d2[m] density: ρ 2[kg/m3] Shear modulus: G[N/m2] |
|
The loss factor and Young's modulus of a single damping material can be calculated by the following calculation when inputting thickness rate d2 / d1 = T, density rate ρ2 / ρ1 = d.
|
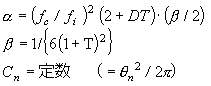 |
This is valid only when
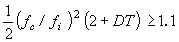 |