What is sound quality evaluation?

What is dB?
(page3)

5. Calculation of decibel value

As we have explained, there are relative level values and absolute level values for decibel values. How do we add or subtract these values?

Possible combinations are as follows.

Relative level value and relative level value
In this case, you can simply add or subtract the decibel value.

[e.g.]

The combined amplification factor of A dB amplifier and B dB amplifier is (A + B) dB.

Absolute level value and relative level value
Again, decibel values are able to be added and subtracted numerically.

[e.g.]

When measuring a sound pressure of 1 Pa (sound pressure level 94 dB) with a sensitivity of -30 dB (re. 1 V/Pa) microphone and an insertion loss of -2 dB preamplifier, a voltage of -32 dBV (approximately 25 mV) is output.

Absolute level value and absolute level value
In this case, numerical addition/ subtraction of decibel value can not be done simply. Regardless of electrical system/ acoustic vibration system, addition/ subtraction by power value is necessary. That is, return the decibel value to an antilogarithm, perform addition and subtraction with an antilogarithm, and then convert it to a decibel value. Such addition is called energy addition (power addition, decibel integration), etc.

For example, the addition value LdB (or subtraction value) of the absolute level value of L₁ dB and L₂ dB is calculated as follows.

Although the addition of absolute level values does not have much meaning, since subtraction is equivalent to the ratio of antilogarithm, the difference in absolute decibels with the same reference value is meaningful as a relative decibel value.
For example, the sound pressure level difference between rooms D, which is often used in the acoustic performance of buildings, is obtained as the difference in decibels as follows.

[e.g.]

The sound pressure level value of the composite of 60 dB and 63 dB is obtained by substituting into equation (5-1) as follows.

When measured under background noise of 40 dB, the sound pressure level was 45 dB. The sound pressure level corrected for background noise at this time can be obtained by assigning to equation (5-1).

When 1/3 octave band filter analysis at 72 dB at 800 Hz, 76 dB at 1 kHz, and 74 dB at 1.25 kHz, the level of 1/1 octave band filter analysis at the center frequency 1 kHz by band synthesis is the following.

Note

The method of adding and averaging on the antilogarithm is also used to obtain the average of the absolute level value.
Such an average is called an energy average (power average, decibel average). For example, the average sound pressure level L dB of the sound pressure levels L₁ dB, L₂ dB, L₃ dB is:

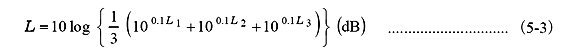For example, the average level of 80 dB, 82 dB, and 84 dB is obtained to be 82.3 dB by substituted into equation (5-3) .
However, depending on existing standards, it may be obtained by numerical average of decibel values.
This method is sometimes called the arithmetic average of decibel values.

In this example, it is 82 dB.
For calculation of decibel value, please refer to Ono Sokki website, "What is sound level meter?" Calculation of deci Bel (dB) "in Chapter 12".

<< Previous page MENU

Reference

1) Ito Kenichi, "Decibel story": Nikkan Kogyo Shinbun, Ltd. (written in Japanese)
2) Sakai Hiroshi, and Suzuki Shusaku "Decibels-How to handle transmission volume": Nikkkan Kogyo Shinbun, Ltd. (written in Japanese)
3) Kuno Kazuhiro "dB consideration": The Acoustical Society of Japan, Technical committees on Noise and Vibration (written in Japanese)
4) Matsuura Hiroyuki "Various dB": Nikkei Electronics (written in Japanese)
5) "What is sound level meter?" Ono Sokki website Technical Report