The damping materials and their performance measurement

Damping materials and their performance measurement
(page1)

1.Damping

“Damping” is reducing the level of vibration on the surface of solid to convert vibration energy into thermal energy, while “vibration isolation” is equivalent to vibration isolation to reduce vibration transmission rate between vibration source and vibration receiving device.
It is necessary to distinguish between damping and vibration isolation.
damping is able not only to reduce vibration itself but also to reduce noise and especially shows effectiveness to reduce vibration near the point of resonance.

damping technology has been studied for long time for the measurement of vibration, while damping materials have more actively studied and developed to apply the noise countermeasure technology.

2.Damping materials

Damping materials are stuck together base materials (steel, wood, concrete, plastics, etc) and viscoelastic materials (resin, rubber, metal, etc). There are unconstrained type (base + damping materials) and constrained type (base + damping materials + binding materials). damping materials (with adhesive tapes) are sold as unconstrained type. Vibration steel plates are sold as constrained type.

3.Loss factor

Loss factor η is one of performance index to measure damping materials. When vibration response attenuates, its stress/ deformation (or load/ displacement) represents hysteresis curve, which is calculated by the loss factor η = K₂ / K₁ by measuring f = K₁ X at the maximum displacement and f = K₂ Χ at the zero displacement. When K1 represents for real number, K₂ represents for imaginary number like fig. 2, K’ is complex elastic modulus, K₂ is storage modulus, K₂ is loss modulus.

Fig. 1

Fig. 2

Although there are various values to indicate damping performance according to electric, mechanical, physics area,
here’re relationships among each values.

	ζ	η	Κ	δ	d	δf	Q	Ψ
ζ	-	2 ζ	ω_Rζ	2 π ζ	aω _R ζ	ω _R ζ / π	ζ /2	4 π ζ
η	η/2	-	ω_R η /2	π η	aω_R η /2	ω_R η /2π	1/η	2 π η
Κ	K/ω_R	2K/ω_R	-	2 π K / ω_R	a K	K /π	ω_R/2K	4 π K / ω_R
δ	δ /2 π	δ / π	ω_N δ /2π	-	aω_N δ /2π	ω_N δ /2π	π /(δ - δ ²)	2 (δ - δ ²)
d	d/a ω_R	2d/a ω_R	d/a	2 π d /a ω_N	-	d /aπ	a ω_R/ 2d	4 π d /a ω_R
δf	π δf/ω_R	2 π δf/ω_R	π δf	2 π ² δf/ω_N	a π δf	-	ω_R2 π δf	4 π ² δf/ω_R
Q	1/2 Q	<1/ Q	ω_R/ 2 Q	π / Q	a ω_R/ 2 Q	ω_R/ 2 π Q	-	2 π / Q
Ψ	Ψ / 4 π	Ψ / 2 π	ω_R Ψ / 4 π	Ψ/2	a ω_R Ψ / 4 π	ω_R Ψ / 4 π²	2 π Ψ	-

Table 1

ζ :	damping ratio, ratio coefficient of viscosity : critical viscosity constant of damping=2 √km
η :	loss factor, k(1+iη) represents elastic items including spring and viscous resistance as complex notation
Κ :	constant of damping, vibration damping of
δ :	logarithm damping ratio, in case vibration amplitude attenuate, adjacent amplitude ratio against natural logarithm
d :	damping degree, vibration damping equivalent to damping value per 1 sec as dB reverberation time (time to reduce signal into 60 dB) T = 60/d
δf:	half band width, which represents frequency near resonance point frequency width represents 1 / √2 of the maximum resonance curve
Q :	the sharpness of resonance equivalent to 2 π times the energy of the vibration system and the energy per cycle given by the external to sustain the vibration
Ψ :	specific damping capacity, ratio loss energy per 1 cycle : gain energy on vibration system

4.Measurement method for damping performance

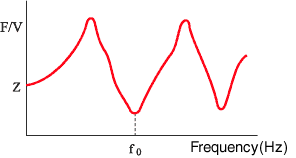
Loss factor, η is the most popular method for the performance index of damping. The classic methods (resonance methods) are the half width method, the damping method, and the mechanical impedance method, while there is non-resonance method as not common.

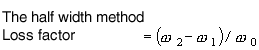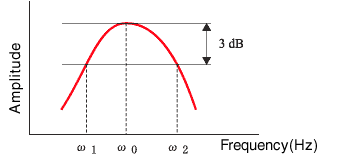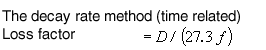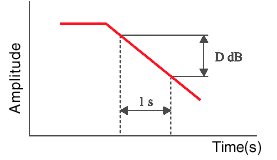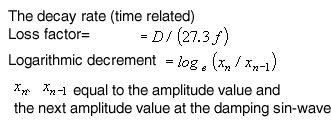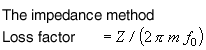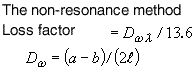<< Previous page MENU Next page >>