Time-Frequency Analysis Software
(Wigner/Wavelet /STFT)
DS-0230
The DS-0230 time-frequency analysis software is intended to perform short-time Fourier transform, Wavelet transform, the Wigner distribution analysis, and other data processing of the time-axis data (with a file extension of .dat or .prn) which is recorded using the software of the DS-2000 Series or FFT analyzers (CF-6400/CF-5000/CF-4200 Series, etc.) from Ono Sokki. Overview of each data processing and comparison is shown below.
Items |
Wigner distribution |
Wavelet transform |
STFT |
|---|---|---|---|
| Time resolution | High | High
frequency: High Low frequency: Low |
Constant |
| Frequency resolution | High | High
frequency: Low Low frequency: High |
Constant |
| Feature | High resolution up to the physical limit | Balanced time and frequency resolutions | Stable result through extended FFT |
| Problem | Existence of cross terms, negative energy |
Result for approximate number of frequencies | Neither time nor frequency resolutions are so high |
| Application | Abnormal vibration analysis of rotational drum of photo copy machine | Voice analysis, image communications | Usual time, frequency analysis |
Wigner Distribution
The Wigner distribution is a new analysis method which enables simultaneous analysis of temporal fluctuation and spatial transition of sudden or unsteady sound and vibration and other complicated waveforms. The Wigner distribution was advocated in quantum mechanics by Dr. E.Wigner in 1932. Then, it was applied to sound analysis by Dr. T.Classen and Dr. Q. Mecklenbraker. In recent year, it has been expected as an analysis method for unsteady state signals. The Wigner distribution with the energy dimension offers high time and frequency resolutions. Therefore, that makes it possible to capture characteristics of transient signals more efficiently than conventional methods. However, negative energy and cross terms appear in many cases which require expertise for interpretation. With the use of the time and frequency distributions of unsteady state signals provided by the Wigner distribution function, the Wigner distribution method is expected as an effective analysis tool for impact sound, abnormal sound, and transient characteristics of audio equipment
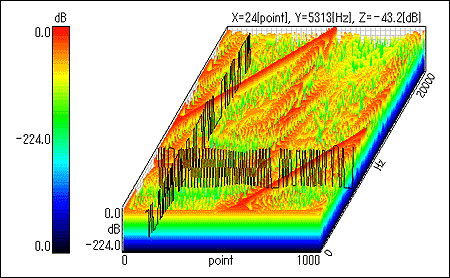
| Time-axis resolution | 200 points |
|---|---|
| Frequency resolution | 256 points (displayed 200 points out of them.) |
| Length of rag window | 1 to 257 points (odd number) can be setup arbitrarily. |
| Analysis time frame length | 16384 points max |
| 3D plot | 3D plot of amplitude (dB) in 64 colors |
| Data reading | By the search point |
| Cross section display | By the search cursor |
Wavelet transform
The Wavelet transform is a new analysis method which enables simultaneous analysis of temporal fluctuation and spatial transition of sudden or unsteady sound and vibration and other complicated waveforms. It is still evolving as a new analysis method. Since an engineer of oil exploration introduced the Wavelet transform as the analysis way of artificial earthquake wave, many academians such as physical scientists, mathematicians, and engineers have tried to apply the Wavelet transform analysis with mathematical basis to various fields With the Wavelet transform, as the term "wavelet" (small waves existing locally) implies, one function is prepared which is existing locally (practically) in terms of time and frequency, the scale transition and shift transition are applied to it, then an obtained set of functions is used as basis functions. The Wavelet transform is a natural analysis method which uses long temporal data in low frequencies (slow fluctuation) and short temporal data for high frequencies (quick variations). Therefore, it is expected as an analysis method for diverse transient phenomena. The distribution of the absolute square value of the Wavelet transform result is called scalogram. The Wavelet transform, DS-0230 time-frequency analysis software, makes it possible to display the signal spectrum as 2D or 3D color image on the time-frequency plane respectively.
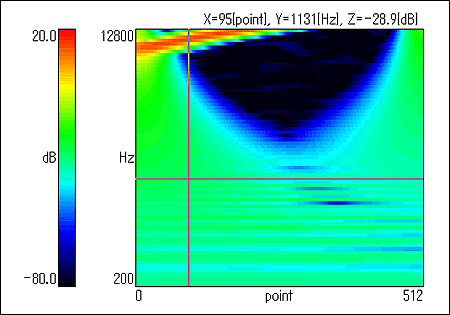
| Mother wavelet | Gabor function |
|---|---|
| Time-axis resolution | 200 points |
| Frequency resolution | 256 points (Displayed 200 points out of them.) |
| Length of rag window | 1 to 257 points (odd number) can be setup arbitrarily. |
| Analysis time frame length | 16384 points max. |
| 3D plot | 3D plot by amplitude (dB) in 64 colors. |
| Data reading | By search points |
| Cross section display | By search cursor |
STFT (Short-time Fourier Transform)
The short-time Fourier transform is an data processing which cuts out signal in short-time intervals and performs the Fourier Transform in order to capture time-depended fluctuation of frequency component of the unsteady state signal. The STFT method is the simplest and easy-to-use analysis method of unsteady state signals. However, in order to improve the accuracy with respect to time-dependent variation (time resolution), it is necessary to shorten the cut-out time period. The accuracy with respect to the frequency (frequency resolution) becomes worse with decreasing cut-out time period. Therefore, the DS-0230 time-frequency analysis software is provided with the function to improve the time resolution while maintaining the required frequency resolution by setting the cut-out time window length and the Fourier transform length separately. The distribution of the absolute square value of the short-time Fourier transform result is called spectrogram.
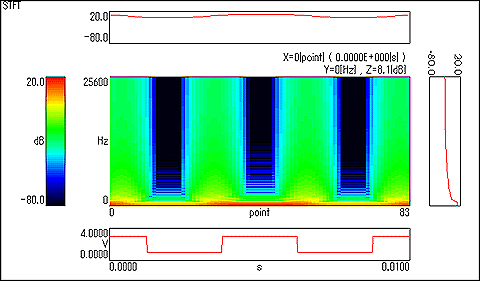
| Time resolution | 8192 points max. |
|---|---|
| Frequency resolution | 2048 points max. |
| Analysis time frame length | 16384 points |
| FFT frame length | 4096 points max. |
| 3D plot | 3D display by amplitude (dB) in 64 colors. |
| Data reading | By search points |
| Cross-section display | By search cursor |
Descriptions and specifications are subject to change without prior notice.
