論理学は、物事を筋道立てて解き明かそうとする学問で、その 1 つに論理代数(ブール代数)があります。 論理代数では、あらゆる事象を真と偽の2
つに分け、それらの組み合わせによって物事の本質を考えていきます。真、偽の対象となる事象を変数といい、A、B、C
といった文字で表します。また、この変数が取る値すなわち真を 1、偽を 0 で表します。
論理変数の組み合わせが論理式といわれ、この式を作るための基本関数として論理積(AND 演算)、論理和(OR 演算)、否定の3種類があります。AND
を取るとか OR を取るなど聞かれたことがあると思いますが、これが論理式のことです。 論理式の変数とその結果を 1 、0
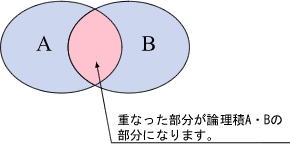
の形で表にしたものを真理値表といいます。 論理積の例で真理値表を説明しますとある領域に変数 A、B
がある時、その要素が「Aでありかつ(AND)Bである」時に、その要素を「A,Bの論理積である」といいます。
<表1>論理和の真値表
(注)AとBが真の時A・Bが1、それ以外の組み合わせでは0になります
デジタルIC回路では、1 つの信号または信号線は例えば 5 V の時 H レベル(High Level 以下 H と記す)、0 V の時を
L レベル(Low Level 以下Lと記す)として考えます。 言い換えると 1 つの信号(変数)は H、Lのうちどちらか
1つのレベルとして出力されますので、例えば1(真)を H、0(偽)をLに意味付けて考えることができます。
先の表1をデジタルIC回路の信号レベルで表すと表2、表3 になります。
<表2>AND 回路の真値表(正論理)
<表3>AND 回路の真値表(負論理)
表2の様に H を 1(真)、L を 0(偽)にとった場合を「正論理」、その逆に表3の様に L を 1(真)、H を
0(偽)に取った場合を「負論理」と言います。
BCD 出力信号は 0 ~ 9 の 10 進数を、2 進化 10 進数(BCD:Binary Coded Decimal) と言われる 4
本の信号線の H、Lの組み合わせで表現します。4 本の線はそれぞれ 2 進数 4 桁として下位の桁から 20 (=1) 、21(=2)、22 (=4)、23 (=8) の各桁に割り当てられています。 1、2、4、8 と一般的に言われる由縁がここに有ります。 例えば 2 進数で 1001
と表された数値は 10 進数では 1×23 + 0×22 + 0×21 + 1×20 =9 になります。BCD コードの真値表を表4に示します。
<表4> BCD コード(2 進化 10 進数)真値表
注)2 進数の組み合わせでは 1111 という数値が考えられますが 2 進化 10 進数では 9 以上の値は有りませんのでエラーとなります
(9 以上は A, B,--- Fなどの文字に割り当ててあるものも有ります)
表4は 1 桁分ですから、10 進 4 桁を BCD で表す場合は 4 桁 × 4 信号= 信号(
本の信号線)で表されることになります。
BCD 出力のカタログ仕様を見ると正論理、負論理の表記があります。正論理と記されている場合は上記(2)項の様に真値の時をH(ハイレベル例えば
5 V)に取っています。また、負論理と記されている場合は真値をL(ローレベル例えば 0 V)に取って出力していることを示します。また、BCD
出力の回路ではオープンコレクタ出力回路が採用されることがあり、オープンコレクタでは最終出力回路にトランジスタが
使用され、そのトランジスタが動作する(ON)、しない(OFF)ことからオン、オフという言葉を使うことがあり、オンは L、オフは H
になります。よってオープンコレクタではオン(L)、オフ(H)と正負論理の関係に注意を払い信号のやり取りする必要が有ります。
次の表は 5 桁の BCD コードを、オープンコレクタ出力負論理の真値表をオン( ON 表示)、オフ( --
表示)で表してみました。ご参考ください。
下欄テキストボックスに表示値を小数点は無視して半角数値で入力の上、[変換]ボタンを押してください。
下の表に出力されるビットが表れます。
再入力は[リセット]ボタンを押してから、入力してください。