Decibels (dB) are used in various fields such as electricity, communication, optics, sound, vibration and so on. Here, we summarize the basic definition of decibel (dB), significance of using it, its convenience, how it is used in various fields, and so on.
The logarithm is used for the definition of decibel (dB). Since understanding the nature of the logarithm is to understand db, we start with a logarithmic explanation.
Note This chapter is intended for a person with liberal arts background. Please skip this chapter if you have a science background. |
When expressing a large number, since the number of digits increases, a power expressions is often used.
For example, a number of 1 million will be expressed as 1 million = 1,000,000 = 10 6.
When expressed by a power of 10, the number of digits is decreased and calculation is simplified.
Generally, when a certain number N is represented by a power of an arbitrary positive number a;
Where, we say that N= am( a>0, a≠1) is an exponential representation of N, a is the base and m is the exponent.
Making this more generalized and extending m to real number as well as integer, the exponential function is obtained.
Important formulas relating to the exponent;
|
Next, you define the logarithm. In equation (2-1), we consider the number of times powers of a that will be N. We call m (the number of powers) the logarithm of N and it is expressed by the following expression.
|
Here, we call m as logarithm, a as base and N as anti-logarithm. It is important to note that m is expressed sometimes different depending on the representation method. The m in expression (2-1) and expression (2-4) are different even if they both are "m". The exponential function is represented centered on N, and the notation represented centered on m is a logarithmic function. They are inverse functions of each other. Speaking in English grammar, it corresponds to a relationship like active and passive.
Substituting m in equation (2-4) into equation (2-1), we obtain the relational expression below.
|
Furthermore, as with the exponential formula, we can obtain an important formula for logarithms.

|
It is said that the logarithm was discovered by John Napier and others in the sixteenth century in order to simplify multiplication and exponentiation calculation. It seemed to be a very useful calculation method in the time without a calculator or a computer.
2-3 Various logarithms due to base difference
What kind of value is appropriate for the base a in equation (2-4) ?
Depending on the base, the following logarithms are used.
Table 1 Various logarithms due to differences in base |
| Base a | Type of logarithm | Field of application |
| 10 | Common logarithm | General technical computing |
| e (Napier's constant) | Natural logarithm | Mathematical analysis |
| 2 | Binary logarithm | Communication theory |
Since common logarithm is mainly used for decibel (dB), main theme in here, logarithm means as common logarithm in this report. In addition, the base a = 10 in Eq. (2-4) is omitted.
[e.g.] The logarithm of 1 million is 6 ⇒ log (1,000,000) = log (106) = 6 |
2-4 Specific logarithmic value
Table 3 in the lower right shows logarithmic values for real numbers from 1 to 10. Although now it is easy to calculate with a calculator, some can be calculated from other values as Table 2 below.
Table 2 "Example of logarithm value"(excerpt) |
|
Figure 1 shows the graph example of common logarithmic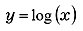 . A numeric example when the antilogarithm x is an integer is shown in Table 3. By the value of antilogarithm x;
. A numeric example when the antilogarithm x is an integer is shown in Table 3. By the value of antilogarithm x;
y< 0 when x < 1
y= 0 when x = 1
y> 0 when x > 1
This means that a decibel value, which is described hereafter, can also be negative.
|
|
The decibel was first used to represent the degree of power transmission attenuation (i. e., ratio) in an electrical system. Now, assume that 2 electric powers are P1 and P2, and ratio of the common logarithmic is x, which is

|
This x is referred to as bell (B). This is due to the fact that the United States Alexander Graham Bell first used it as a representation of the transmission attenuation of power in the phone. Also, since bell (B) itself is too large, decibel (dB), which is 1 tenth of its value, is commonly used.
Note The "Bell (B) itself is too large" means that the quantitative value of 1 bell is large, but it is numerically small. For example, 7 B will be the same amount as 70 dB. This is easier to understand when compared to a length of 1 m and a length of 1 mm. |
Decibel L is defined as 10 times the logarithm of the electric power ratio between two points (P1, P2).
 |
In this way, although the definition of dB is originally the electric power ratio, it is also commonly used for voltage ratio (or current ratio). Since the power is proportional to the square of the voltage (or current), so it becomes
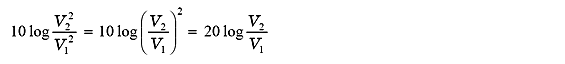 |
Therefore, a decibel [L] at voltage ratio is defined as 20 times the logarithm of the voltage ratio between 2 points (V1, V2).
 |
In this way, the same decibel value is obtained regardless it is the ratio of electric power (power) or the ratio of voltage (effective value or linear value).
Note Physical signals such as electricity and sound (vibration) are usually AC signals. In this document, the physical quantity used in the decibel calculation is its effective value.
In the transmission circuit theory calculation, sometimes Nepa (Np) is used that uses natural logarithmic. When the natural logarithm is represented as ln, it can be converted to;
1 Np is equivalent to 8.686 dB. Napa is taken from Napier, who invented the logarithm as it is described in the previous chapter 2. |
Table 4 shows the relationship between the commonly used decibel value and the antilogarithm (power ratio and voltage ratio). By using this table, it is easy to obtain the decibel value (approximate value) for the magnification of the voltage
Table 4 Frequently used decibel value and its converted value |
| dB value | -20 | -6.02 | 0 | 3.01 | 6.02 | 10 | 20 | 30 | 40 |
| Electric power ratio | 0.01 | 0.25 | 1 | 2 | 4 | 10 | 100 | 1,000 | 10,000 |
| Voltage ratio | 0.1 | 0.5 | 1 | 1.41 | 2 | 3.16 | 10 | 31.6 | 100 |
[e.g.] How about 5 times? |
Note As shown in Table 4 above, when the antilogarithm value is greater than 1, the dB value is a positive value. When the antilogarithm value is less than 1, the dB value is negative. This is the logarithmic property itself as described above. That is, even if the decibel value is negative, the antilogarithm value itself is not a negative number, but only the electric power ratio (or voltage ratio) is smaller than 1. |
3-3 Decibel representing absolute value
Decibel, as also defined, represents the ratio of the two quantities, which simply means the relative level value. If the reference value (the denominator of the ratio) is defined as a fixed physical quantity, the decibel value in that case can be easily converted as the absolute value of the physical quantity, so it can be regarded as an absolute level value.
Generally, the magnitude of the physical quantity expressed in decibels in the field of electricity and sound (vibration) is called "level (unit dB)". From here, the level and decibel are explained as almost the same meaning.
Considering an example of expressing a voltage value is shown below.
When the reference value of voltage ratio is defined as 1 V , an arbitrary voltage value can be expressed by a decibel value.
The unit in this case is dBV.
For example, if x (V) is y (dBV);
 |
You can omit reference value 1 during calculation.
Note Hereafter, if the absolute standard value is 1, then the value 1 is omitted in the definition formula of the absolute level value. That is, the value of the voltage ratio in table 4 above can be considered as the voltage value.
This absolute level value is used to express the voltage range value of the input part in the FFT Analyzer (see Table 5). |
The exact same can be said for other physical quantity. Consider, for example, an example of vibration acceleration. If the reference value is defined as 1 m/s2, then 5 m/s2 means about 14 dBm/s2.
In the example so far, the reference value was 1, so calculation was simple. However, the reference value defined by the sound pressure level often used in the acoustics field is not 1. Even in this case, the decibel value expresses the absolute value (sound pressure value) in the same way.
This will be described later. The decibel itself is not a unit of SI unit systems, but in the acoustics field decibel is used as a quantity conforming to the unit.
In summary, it can be said that the absolute level value represents the physical quantity itself, considering dB as a unit. So, there are many cases that it is written as "dB ○ ○" instead of simply "dB".
As you can see in the explanations so far, there are many advantages of using decibels. The following is a typical reason.•When expressing large numbers such as the gain of the amplifier, using decibels can express it with fewer digits.
Forexample, 50,000 times is 94 dB.
•When characteristic evaluation is performed, such as a multistage amplifier or a plurality of transmission systems,
the calculation can be easily performed because multiplication and division can be replaced by addition and subtraction.
•Weber-Fechner law " The perceived intensity is proportional to the logarithm of the stimulus. ", which is suitable for evaluation of sensory
values (especially acoustics).
3-5 Decibel (dB) and percent (%)
Decibels and percentages (percent,%) also represent ratios, mutual conversion of numbers is possible. The decibel in this case is usually considered as voltage ratio. For example, 10 % is -20 dB from 20 log (10/100) = - 20.
When expressing the resistance tolerance error and the tolerance of the frequency characteristic range of the sensor, it may be expressed as a ratio from a reference value such as ±5 %. This number can also be converted to decibel value.
For example, +10 % is (1 + 10/100) times, so it corresponds to 0.83 dB, from 20 log (1.1) = 0.83. Similarly, -10 % is equivalent to 20 log (0.9) = -0.92, and -0.92 dB.
Here, note that % is linear and dB is logarithmic.
+1 dB ⇒ +12.2 %
-1 dB ⇒ -10.9 %
Equations such as the above are established. When it is logarithmically equally spaced, the linear interval is wider on the + side. In a very rough way of saying, ±1 dB is about ±10 %.