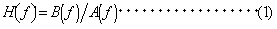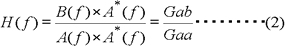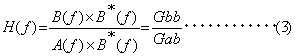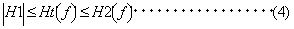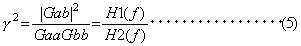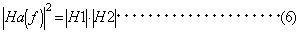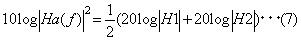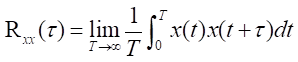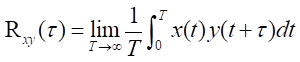FFT解析に関する 基礎用語集

周波数応答関数（伝達関数）は、電気系や、構造物の振動伝達系などの入力と出力との関係を表したもので、入力のフーリエスペクトル   と出力のフーリエスペクトル   の比で表されます。

すなわち、周波数応答関数 は

本器では、上式右辺の分母、分子に   の複素共役 をかけて、次式のように計算をしています。

分母の は のパワースペクトル、分子の は と   のクロススペクトルです。このことから周波数応答関数   は入出力のクロススペクトルを入力のパワースペクトルで割算して求めることができます。

次の計算方法でも、周波数応答関数を推定することができます。

(2)式で推定される伝達関数を Ｈ1、(3)式で推定される伝達関数を Ｈ2 と呼びます。

いま、真の伝達関数を   とすると、入力と出力の両方に雑音が多い場合は、

の関係になります。（ただし、系は線形系であるとします。）　また、位相に関しては、 とも同じくクロススペクトル の位相と等しくなります。

コヒレンス関数との関係は

となります。 は と との比となります。入出力のパワースペクトルの比（伝達特性）を とすると

ですから、

あるいは対数をとって

となります。すなわち、ととのゲインの対数値の平均は、周波数応答特性の対数値と等しくなります。

周波数応答関数は、ゲイン特性と位相特性で表されます。ゲイン特性は、系を信号が通過することによって振幅がどう変化するかを表すもので、Ｘ軸は周波数、Ｙ軸は のデシベル（入力に対する出力の振幅比）で表示されます。また、位相特性は入力信号と出力信号との間での位相の進み、遅れを表すもので、Ｘ軸は周波数、Ｙ軸は度またはラジアンで表示されます。

周波数軸での微分演算は、パワースペクトルでは(ω)ⁿ、周波数応答関数では(jω)ⁿを乗算することにより行われます。
(j は虚数単位、ω＝2πｆ)

(注意1)パワースペクトルで、一階微分がωの2乗で二階微分がωの4乗なのは、パワー値だからです。

(注意2)周波数応答関数は複素数演算だから虚数単位jも乗算されます。

周波数軸での積分演算は、パワースペクトルでは(ω)ⁿ、周波数応答関数では(jω)ⁿで除算することにより行われます。
(j は虚数単位、ω＝2πｆ)

(注意1)パワースペクトルで、一重積分がωの2乗で二重積分がωの4乗なのは、パワー値だからです。

(注意2)周波数応答関数は複素数演算だから虚数単位jも除算されます。

周波数分解能は、その時の周波数レンジを分析ライン数（解析データ長 ÷ 2.56)で割った値になります。例えば、周波数レンジが10 kHzでサンプル点数（解析データ長）が4096の時は、分析ライン数が1600ラインとなりますから、周波数分解能Δfは、6.25 Hz（＝10000/1600）となります。

ズーム解析時での周波数分解能は、（周波数スパン）÷分析ライン数となります。

変動する時間軸信号の瞬時値がある振幅レベル以下にある確率を表します。振幅確率分布関数は振幅確率密度関数を積分することにより求められます。

振幅確率密度関数は、変動する信号が特定の振幅レベルに存在する確率を求めるもので、横軸は振幅（Ｖ）、縦軸は０から１で正規化されます。本ソフトでは振幅を電圧レンジの 1／512 に分解します。振幅確率密度関数から入力信号がどの振幅付近でどの程度の変動を起こしているかが解析でき、その形状による合否判定等に利用することができます。

通常のFFT 解析では、０から周波数レンジまでの範囲をライン数分（例えば 800ライン）解析しますが、任意の中心周波数で、ある周波数スパンで分析する機能がズーム機能です。この機能を使うことにより、高い周波数帯域でも、高周波数分解能（Δfが小さい）の分析が可能となります。このときデータの取り込み点数はズーム倍率分必要になるので、時間がかかります。

自己相関関数と相互相関関数があります。

自己相関関数は、波形 ｘ (ｔ )とそれを τ だけずらした波形 ｘ (ｔ＋τ )を用いたずらし量 τ の関数で、次式のように定義されます。

自己相関関数は波形の周期を調べるのに有効です。自己相関関数は τ＝０ すなわち自身の積をとったときに最大値となり、波形が周期的ならば、自己相関関数も同じ周期でピークを示します。また、不規則信号では、変動がゆっくりならば τ が大きいところで高い値となり、細かく変動するときはτが小さいところで高い値を示して、τ は変動の時間的な目安となります。

パワースペクトルの逆フーリエ変換により自己相関関数を求めています。

相互相関関数は２つの信号のうち一方の波形をτだけ遅延させたときのずらし量 τ の関数で、次式のように定義されます。

相互相関関数は２信号間の類似度や時間遅れの測定に利用されます。もし、２信号が完全に異なっているならば、τ に関わらず相互相関関数は０に近づきます。２つの信号が、ある系の入力、出力に対応するものであるときに、その系の持つ時間遅れの推定や、外部雑音に埋もれた信号の存在の検出および信号の伝播径路の決定などに用いられます。

クロススペクトルの逆フーリエ変換により求めています。