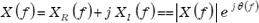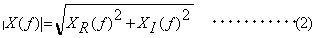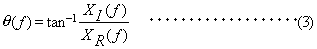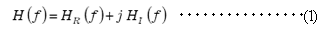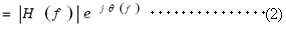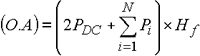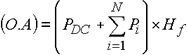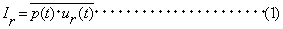FFT解析に関する 基礎用語集
ウィグナー分布 |
|---|
ウィグナー分布は量子力学の分野において、E. Wigner により提唱されたものであり、非定常信号に対して拡張されたパワースペクトルというような性質をもつものです。従来のFFTでは時間分解能―周波数分解能が相補的な性質(周波数分解能を上がるとサンプル時間が長くなる。)を有しているため、非定常的な信号の瞬時的なスペクトルを良好な分解能で求めることは困難でしたが、これに対しウィグナー分布では時間分解能―周波数分解能の相補的な制約を直接受けないため、周波数―時間平面上でパワースペクトルの良好な時間―周波数分解能を得ることができます。しかしながら、計算点数がFFTと比較して非常に多いことから、実用的ではありませんでした。Oscope 時系列データ解析ツール(ソフト)のオプション OS-0263 時間-周波数解析ソフトを使用することで、ウィグナー分布の解析ができます。 |
エイリアシング(折返しひずみ) |
|---|
| サンプリング定理では信号の最高周波数成分に対し2倍以上の速度でサンプリングすることが必要であり、サンプル周波数の1/2の周波数をナイキスト周波数といい、ナイキスト周波数以上の成分が信号に含まれていると、エイリアシング(折返しひずみ)が生じます。 |
エネルギースペクトル密度(Energy Spectral Density) |
|---|
| 打撃法などによるインパルス状の有限なエネルギーに対し、これをエネルギーで規格化して表示します。 これは、パワースペクトル密度にさらに取り込み時間(ウィンドウ長、T=1/⊿f)をかけることにより求めます。 |
オーバーラップ処理 |
|---|
リアルタイム解析周波数以下の場合ウィンドウをオーバーラップして、FFT 解析を実行できます。 例えば1024点ごとのデータをFFT 処理しますが、このとき、新しくサンプリングされたデータと以前のデータと重ねて(オーバーラップして)FFT 解析を 実行します。オーバーラップ量が大きいということは、それだけ信号時間の変化をより細かく計測できることになります。 |
オービット(リサジュー) |
|---|
2つの信号を直交するx,y軸上で合成した図形をオービットまたはリサジューといい、2信号の振幅、周波数比、位相差の組合せによって視覚的な特長を示します。また、周波数比が整数のときには描かれる図形の軌跡は一定の周期で元に戻ります。 |
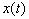 のフーリエ変換は;
のフーリエ変換は;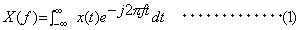
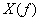 を本器では特に(複素)フーリエスペクトルと呼びます。
を本器では特に(複素)フーリエスペクトルと呼びます。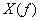 は複素関数であるので、実数部と虚数部より、振幅と位相として表すことができます。
は複素関数であるので、実数部と虚数部より、振幅と位相として表すことができます。