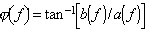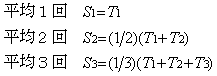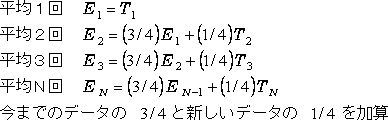FFT解析に関する 基礎用語集
ナイキスト線図 |
|---|
|
周波数応答関数(伝達関数)の実数部を横軸に、虚数部を縦軸にとり、周波数に関して描かれたものをナイキスト線図といい、主に制御系の安定性の判別に利用します。 |
ニコルス線図 |
|---|
|
縦軸をゲイン、横軸を位相として、周波数応答関数(伝達関数)を表示します。 |
波高率(クレストファクター: Crest Factor) |
|---|
波形のピーク値と実効値の比(ピーク値/実効値)で定義されています。DC の波高率(クレストファクター)は”1”、正弦波のクレストファクターは、√2 = 1.414 となります。 例えば、ピーク値や実効値では、ベアリングの大きさによって振動値も相対的に変化しますが(大きなベアリングは振動の実効値も大きく、異常状態の場合のピーク値もさらに大きくなります)、クレストファクタ値はピーク値と実効値の比を求めているためベアリングの大小に振動値が左右されず、傷等の異常度合いをより正確に判断することが可能となります。計測されたクレストファクタの値が大きいと異常度合いが大きいと判断します。 |
パワースペクトル |
|---|
|
信号のパワーを一定の周波数帯域毎に分割し、その帯域毎のパワーを周波数の関数として表したものをパワースペクトルといいます。単位は振幅の2乗(V2 rms)となります。 FFT アナライザーでは、フーリエ変換によって、時間軸波形から周波数軸波形を求めています。時間関数 x (t )のフーリエ変換対は次式で表されます。
複素関数 X (f )は、時間関数 x (t ) フーリエスペクトルです。また、上の関係式で示されるように、フーリエスペクトルがわかっていれば、元の時間軸波形を再生することができます。 実際には、有限のサンプル値から数値計算を行うため、離散フーリエ変換(Discrete Fourier Transform)を行っています。FFT アナライザーでは、高速フーリエ変換(Fast Fourier Transform)を用いていますが、これはDFTを高速演算する算法です。 パワースペクトルの次元は(V2 rms)ですが、本機では、リニアスケールのとき√(V2 rms)としています。したがって、その周波数の時間波形の実効値と一いたします。メニューにより(V2 rms)の表示も可能です。 初期状態では、X軸は周波数、Y軸は1(V2 rms)を0(dBV rms)とする対数スケールで表示されます。 |
パワースペクトルのリニア/ログ換算 |
|---|
|
下欄ボックスに半角数値を入れて、元の単位ボタンを押してください。 下の段にそれぞれの単位に換算した値が出ます。
V rms : パワースペクトルのリニア表示時の実効値 計算は; V0-p = √2×V rms dBVr = 10 LOG{Vrms /(基準)}2 = 20 LOG (Vrms) [基準は実効値 1 Vrms] で行なってます。 なお、計算値は有効桁の関係から真値と完全には一致しない場合があります。 |
パワースペクトル密度(Power Spectral Density) |
||||||
|---|---|---|---|---|---|---|
|
デジタルFFT アナライザーでは分析周波数レンジによりバンド幅(⊿f )が異なります。たとえば 1/800 分解能のとき、20 kHzレンジでは 20 kHz/800=25 Hzがバンド幅に相当します。 ここで、ホワイトノイズなどの広帯域にわたる(分布する)信号を周波数分析すると、そのパワーは、バンド幅ごとの積分値として得られます。したがって、分析レンジを変更すると、この値が変化し比較できません。そこで、以下の方法により単位周波数(1 Hz)あたりのパワースペクトルを求め、これをパワースペクトル密度(略してPSD)といいます。ただし、ラインスペクトルの信号では意味はありません。 パワースペクトル密度は、以下で計算されます。
ここで
すなわち、各ウィンドウに対応したバンド幅で得られたパワーを規格化しています。また、このパワースペクトル密度を求める場合はなるべくハニングウィンドウまたはレクタンギュラウィンドウにて測定してください。 |
ヒルベルト変換 |
|---|
|
実関数 f (t ) のヒルベルト変換 g (t) は(1)式で定義され、逆ヒルベルト変換は(2)式のよう定義されます。
ここで、*は畳み込みを表す。 ここで、実関数 f (t ) より、ヒルベルト変換を用いて(3)式の解析信号(複素数) Z (t ) を定義します。
Z (t ) は複素数であるから、ベクトル表示すると
ここで
r (t )は、f (t ) の振幅(エンベロープ)、θ (t ) は瞬時位相と呼ばれます。すなわち任意の実関数 f (t ) は
と表すことができます。 このように、ヒルベルト変換を利用することにより、 f (t ) のエンベロープを求めて、それより対数減衰率(さらには減衰比)を計算することができます。 エンベロープはシステムの瞬時のエネルギーの時間変化を表します。さらに、 f (t ) を単に振幅だけではなく、瞬時位相というもう一つのパラメーターから観測することができます。 θ (t ) を微分して
瞬時周波数とする見方も可能です。 軸は周波数、Y軸は1(V^2 rms)を0(dBV rms)とする対数スケールで表示されます。 |
フーリエ変換 Fourier Transform |
|---|
|
変域
一方、時間関数 x (t ) を定義する時間区間長Tを無限に長くしたときの(1)、(2)式の極限を求めるために、(3)式のような変換を両式に施すと、(2)式の積和は積分に置き換わり、(4)、(5)式のような変換対が得られる。
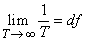 , ,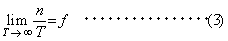
(4)式は、x (t ) のフーリエ変換、(5)式は X (f ) の逆フーリエ変換と呼ばれ、この一対の式はフーリエ変換対、またはフーリエ積分対といわれる。なお、周波数 f の関数である X (f ) は複素振幅(またはフーリエスペクトル)とも呼ばれる。(4)、(5)式から明らかなように、フーリエ変換は、時間関数からそれに対応する周波数関数を求め、逆フーリエ変換は、周波数関数から時間関数を求めるものである。 また、時間関数 x (t ) の始点を時間軸の原点として、 x (t ) がt<0の区間では0であるとして、フーリエ変換の積分区間を半無限区間とした次のような変換対が使われることもある。
いま、(4)式で定義される周波数の複素関数 X (f ) を、(8)式のように表すと、時間関数 x (t ) を形成する周波数fの成分は、(5)式の定義から(9)式となる。
すなわち、周波数 f の成分の振幅は2|X (f )|、位相は X (f ) の偏角 ∠X (f ) となる。このように、時間関数 x (t ) の周波数fの成分の振幅と位相は、複素数 X (f ) から求められることから、X (f ) は x (t ) の周波数スペクトルと呼ばれる。 また、(1)式で求められるフーリエ係数は、周波数n/Tだけで値をもち、他の周波数では常に0になることから、線スペクトルといわれる。これに対して、(4)式の X (f ) は周波数の連続関数であるから、連続スペクトルといわれる。 |
平均化処理 |
||
|---|---|---|
|
平均化処理の種類 ・加算平均、ノーマライズ加算平均
N回の加算平均
・指数平均 指数平均の場合、回数の設定ではなく最新データの重みづけの数値を設定します。 この数はアナログのRCフィルターの時定数に相当します。 N=4のとき
・ピークホールド パワースペクトルのピークホールドを行います。ピークホールドスタートからポーズまでの各周波数ラインごとの最大値をホールド(記憶)します。 また、このピークホールドに連動して、マックスオーバーオール機能があります。これは、オーバーオールのピークホールド機能と考え、オーバーオールが最大値であったときの瞬時のパワースペクトルを記憶する機能です。 このピークホールドモードには、平均化回数設定はありません。したがって、平均化モードにおいてスタートおよびポーズ(ストップ)の操作を必要とします。すでに平均化回数が設定されていてもピークホールドには関係ありません。また、このピークホールド実行時も、CRTの実行回数が増えていきます。これは、FFT 演算の回数を示しています。
・減算平均 減算平均は、加算平均後のパワースペクトルからパワースペクトルを減算する機能です。 [計算式] 例)減算平均 N=20 Si:i 回目の減算平均結果(表示) S :減算されるパワースペクトル(以前に加算平均より求めたパワースペクトル) Pi:i 番目のパワースペクトル 減算平均スタート ↓
・スイープ平均 サイン信号を使用して、低い周波数から高い周波数までスイープして、その信号に応じてFFT 演算を行います。 スイープ平均では、1回の取り込みごとにマスタチャンネル側で最大のスペクトル(1ライン)を検出し、その1ラインについてのみ計算します。そのラインのみ更新します。 外部スイープ信号のスイープ速度が演算処理時間より速い場合、求められないスペクトルラインが生じます(歯ぬけ)のでご注意ください。
平均化処理できる領域と種類 ・時間領域平均 加算平均、指数化平均
・周波数領域平均 加算平均、指数化平均、ピークホールド、減算平均、スイープ平均
・振幅領域 加算平均 |
ボード線図 |
|---|
|
周波数応答関数 H(f) のゲイン特性と位相特性の2つを1組とする周波数特性表示をボード線図といいます。ゲインの縦軸は、20log10 (H(f)) のデシベル(dB)単位、位相は degree またはラジアンで表します。 |
モーダル解析 |
|---|
|
あらゆる構造物(機械、建物、自動車、自転車、家電製品 等)は、それぞれ固有振動数をもっています。そこで、固有振動数およびそれ以外の周波数の振動においても、構造物がどのように振動するかを知っておく必要があります。モーダル解析は、各種構造物に各周波数の振動を与えた場合の状態をシミュレーションするソフトですが、現在、FFT アナライザーと加振器、振動ピックアップを組み合わせることにより求めた各構造物上の伝達特性からパソコン等により、モーダル解析が簡単に行えます。これにより構造上の弱点を見つけ、防振、防音などの対策を効果的に行うことができます。 |
リアルタイム解析 |
|---|
|
リアルタイム解析とは、サンプリングされたデータに対して、ウィンドウとウィンドウの間があくことなく連続してFFT 演算が行われる解析状態のことです。 通常のFFT 解析では信号の解析データ長分(1024点または2048点)のサンプリングを行うと次にそのデータに対してFFT 演算を行いますが、その間に次のデータを取込んでおき、前の演算が終るとすぐに次の演算を行う方式となっています。サンプリングにかかる時間よりFFT 演算時間(表示時間までを含む)のほうが短ければリアルタイム解析が実行できます。これに対して演算時間がサンプリング時間より長くなると演算している間に1フレーム分以上の新しい信号がサンプリングされてしまい、信号の取りこぼしが出てきます。また逆に演算時間よりサンプリング時間の方が長いときには、ウィンドウの一部を前のウィンドウと重ねること(オーバーラップ処理)ができます。 |
リフタードエンベロープ |
|---|
|
ケプストラムの、短ケフレンシー部分を逆フーリエ変換することにより、対数パワースペクトルのエンベロープ(包絡線)が求まります。(リフタードエンベロープ)このエンベロープは系特有のもので、入力信号のスペクトルには依存しません。 応用として、音声波、生体波などからの基本周波数およびスペクトルエンベロープの抽出などがあります。 |
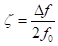
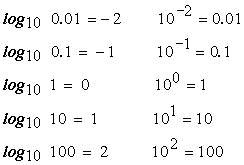
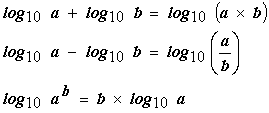
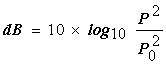
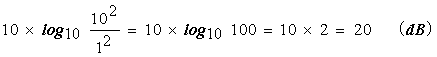
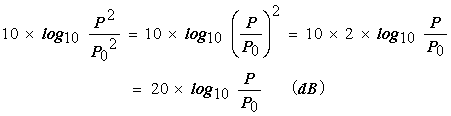
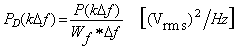
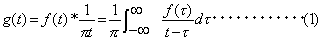
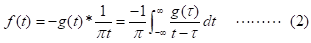
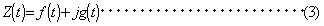
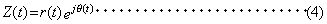
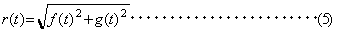
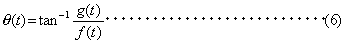
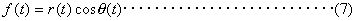
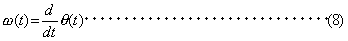
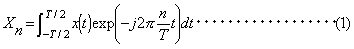
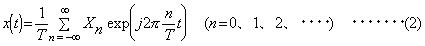
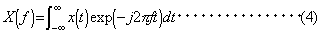
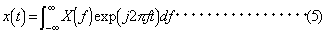
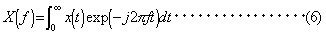
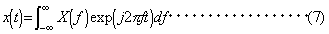
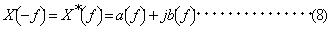
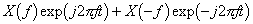
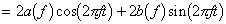
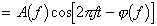
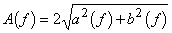 ..............(9)
..............(9)