3. Fourier Series and Fourier Transforms
As mentioned in the previous report, waveforms that periodically vary in the time domain can be expressed using a Fourier series. In this chapter we will actually try to express these periodical waveforms by using the Fourier series and Fourier transform.
Let us begin by considering the sound "A" (pronounced as "aah"), as introduced in Figure 1-1, Chapter 1, of the previous report.
As we noted, the sound "A" could be decomposed into three elements, "A1", "A2" and "A3". Moreover, the waveform of "A1" could be represented as cosine waves having a phase difference in the following manner:
|
Similarly, "A2" and "A3" are also expressed as follows:
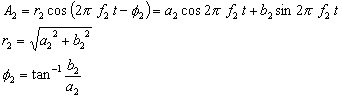
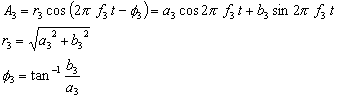
Since the sound x(t) of "A" is composed of the waves of "A1", "A2", "A3" ..., the following relation holds:
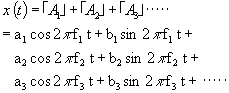
By rearranging f1, f2, f3, ..., a1, a2, a3 ..., and b1, b2, b3, ... , respectively, as fn, an, bn, (n = 1, 2, 3, ...) here, we have:
|
If we compare Equation 3-1 for the sound "A" with Definition Formula 3-2 for a Fourier series, shown below, we notice the two are strikingly alike. If the basic frequency is f0, components f1, f2, f3, --- of the sound "A" are f1 = f0, f2 = 2f0, f3 = 3f0, and correspond to the 1st harmonic, 2nd harmonic, 3rd harmonic, --- (frequencies in integer multiples of f0). Since the example analysis of the sound "A" in Figure 1-2 of the previous report adopted T = 160 ms (f0 = 6.25 Hz), these harmonics correspond to f1 = 106.25 Hz = 17f0 (17th harmonic), f2 = 34f0, and f3 = 51f0, in the figure. The harmonics that do not correspond to f1, f2, f3, --- can be considered other signal elements different from "A", such as background noise.
As can be gathered from the above, the concept we have discussed since Section 2-2 of the previous report is nothing other than the Fourier series.
So, let us take a look at the definition formula of this Fourier series.
If the period of a waveform periodically varying in the time domain is represented by T, we have:
Fundamental frequency f0 = 1/T
Fundamental angular frequency ![]() 0 = 2
0 = 2![]() f0
f0
Therefore, the waveform can be expressed in the form of a Fourier series as shown below:
|
Here, by making use of the multiplications of cosine and sine given in Section 2-6 of the previous report, and the appropriate area values, the components of Equation 3-2 can be found:
|
a0 is a DC component, and an and bn are the amplitudes of cosine waves and sine waves whose angular frequency is n![]() 0. These last two are called Fourier coefficients and are collectively referred to as a Fourier coefficient pair.
0. These last two are called Fourier coefficients and are collectively referred to as a Fourier coefficient pair.
Now, let us review the explanation thus far.
Equation 3-2 can be interpreted as follows:
n![]() 0t(n=1, 2, 3, ...) are 1x, 2x, 3x, ... harmonics of basic angular frequency
0t(n=1, 2, 3, ...) are 1x, 2x, 3x, ... harmonics of basic angular frequency ![]() 0, where the waveforms of the components of n
0, where the waveforms of the components of n![]() 0t are expressed by:
0t are expressed by:
|
The corresponding Fourier coefficients an and bn can be found by Equation 3-3. Furthermore, based on the relationship between an and bn shown in Figure 3-1 below, Equation 3-3 can be represented as follows:
Figure 3-1 |
|
Where rn and ![]() n are the amplitude and phase of the n-th harmonic, respectively.
n are the amplitude and phase of the n-th harmonic, respectively.
An FFT analyzer stores the calculated Fourier coefficients an and bn in memory, then uses them to calculate the amplitude rn and phase ![]() n of frequency fn. Based on this calculation, the analyzer produces a spectral display showing the relationship between frequency fn and amplitude rn. Likewise, it gives a phase spectrum showing the relationship between frequency fn and phase fn. The original time waveform can also be restored from an and bn using Equation 3-2. We should note that a spectrum is just a quantity of magnitude (i.e., does not have the phase information <
n of frequency fn. Based on this calculation, the analyzer produces a spectral display showing the relationship between frequency fn and amplitude rn. Likewise, it gives a phase spectrum showing the relationship between frequency fn and phase fn. The original time waveform can also be restored from an and bn using Equation 3-2. We should note that a spectrum is just a quantity of magnitude (i.e., does not have the phase information <![]() >) and, therefore, spectral data alone does not enable the original waveform to be restored. Among its functions, the FFT analyzer offers a technique to seek time waveforms from Fourier transform data (i.e., an inverse Fourier transform). To execute this function, it is necessary to store previously a Fourier spectrum with phase information (consisting of a real part and an imaginary part). In addition, if original waveforms are stored, the analyzer is also able to perform an FFT from this data again.
>) and, therefore, spectral data alone does not enable the original waveform to be restored. Among its functions, the FFT analyzer offers a technique to seek time waveforms from Fourier transform data (i.e., an inverse Fourier transform). To execute this function, it is necessary to store previously a Fourier spectrum with phase information (consisting of a real part and an imaginary part). In addition, if original waveforms are stored, the analyzer is also able to perform an FFT from this data again.
* The terms "real part" and "imaginary part" will be explained in the following section.
3-2 Representing the Fourier Series by Complex Exponential Function
An FFT analyzer will display the expressions "Real Part" and "Imaginary Part" when indicating Fourier spectra and transfer functions among the diverse types of functions it computes and processes. These expressions appear when a Fourier series is represented by a complex plane (Gauss plane) and are used in a technique for functional representation. Each part has an important meaning. In this section we will attempt to transform a Fourier series into an indication of complex exponential function by using Euler's formula and will, in this way, explain the concepts of "Real Part" and "Imaginary Part."
The explanation below may be a bit hard to understand, but let's start by gaining an understanding of Figure 3-3 below. Here, we will not go into details of the complex number and exponent; those who wish to know more about them should refer to the relevant specialized literature.
Euler's formula is:
|
In Euler's formula indicated above, ![]() , e and j are understood as follows:
, e and j are understood as follows:
![]() : Pi, 3.141592....
: Pi, 3.141592....
e : Base of Napierian logarithm, e = 2.71828.... et is "et", whether differentiated or integrated. d/dt (e t ) = e t
j : Value where j2 = -1.
As you are well aware, numbers consist of real numbers and imaginary numbers. Those without a j value are called real numbers, and those with a j value are termed imaginary numbers.
The complex number Z = 1+1j on a complex plane (Gauss plane) is expressed as shown in Figure 3-2(a). Meanwhile, X = ejn![]() t represents a circle having radius = 1 on a complex plane as indicated in Figure 3-2(b), which circle rotates counterclockwise (i.e., in a positive direction) at an angular speed of n
t represents a circle having radius = 1 on a complex plane as indicated in Figure 3-2(b), which circle rotates counterclockwise (i.e., in a positive direction) at an angular speed of n![]() per second. This means that the two equations of cosine and sine that represented the locus of a ball in Equations 2-7 and 2-8 (given in the previous report) are represented here by one single equation. Similarly, Y = e-jn
per second. This means that the two equations of cosine and sine that represented the locus of a ball in Equations 2-7 and 2-8 (given in the previous report) are represented here by one single equation. Similarly, Y = e-jn![]() t - indicates a clockwise (negative) rotation. X and Y relate to each other symmetrically with respect to the real-number axis (Re-axis), Y being called a conjugate complex number of X and X, a conjugate complex number of Y. Conjugate complex numbers are indicated with an "*", e.g., Z*.
t - indicates a clockwise (negative) rotation. X and Y relate to each other symmetrically with respect to the real-number axis (Re-axis), Y being called a conjugate complex number of X and X, a conjugate complex number of Y. Conjugate complex numbers are indicated with an "*", e.g., Z*.
Figure 3-2 |
We rearrange Equation 3-5 above by substituting it into Fourier-series Equations 3-2 and 3-3, as follows:
|
Multiplying both sides by j yields the following:
|
Noting (an-jbn) and (an+jbn) here, we express X0, Xn, Xn*, respectively, as follows:
|
(Equation 3-7) |
| (Equation 3-7a) | |
| (Equation 3-7b) | |
| (Equation 3-7c) |
Considering the case where n = 0 is adopted in Equation 3-7b above, the right side of Equation 3-7b matches that of Equation 3-7a, because e0 = 1. Therefore, Equation 3-7 can be rewritten as follows, assuming that n takes n = 0 to ![]() :
:
|
Moreover, if we assume that n in Equation 3-7c takes n = -1 to - ![]() , it matches the right side (n = 1 to
, it matches the right side (n = 1 to ![]() ) of Equation 3-7b. Therefore, Xn* can be handled as one that exists when n of Xn is n = -1 to -
) of Equation 3-7b. Therefore, Xn* can be handled as one that exists when n of Xn is n = -1 to -![]() . Accordingly, to recap the above, Equations 3-7, 7a, 7b and 7c can be represented in a very clear form as follows:
. Accordingly, to recap the above, Equations 3-7, 7a, 7b and 7c can be represented in a very clear form as follows:
|
|
Equation 3-9a above is termed the Fourier series of a complex exponential indication and Equation 3-9b, the Fourier expansion of a complex exponential indication.
Because ejn![]() 0t and e-jn
0t and e-jn![]() 0t in Euler's formula consist of a cosine and sine, this formulation replaces the periodicity of cosine and sine we have seen to this point, and has the nature of an exponent at the same time. If we replace ejn
0t in Euler's formula consist of a cosine and sine, this formulation replaces the periodicity of cosine and sine we have seen to this point, and has the nature of an exponent at the same time. If we replace ejn![]() 0t and e-jn
0t and e-jn![]() 0t with sine and cosine, respectively, for example, and replace Equation 3-9b with cosine, it corresponds to the equation for an in Equation 3-3. Furthermore, if we consider that the cosine term and sine term of a Fourier coefficient are the real part and imaginary part of a complex number indication, in light of the relation shown below, then it will be easier to understand the relationship between the Fourier series and its complex number indication. (To see this, compare Figure 3-1 and Figure 3-3 with each other.)
0t with sine and cosine, respectively, for example, and replace Equation 3-9b with cosine, it corresponds to the equation for an in Equation 3-3. Furthermore, if we consider that the cosine term and sine term of a Fourier coefficient are the real part and imaginary part of a complex number indication, in light of the relation shown below, then it will be easier to understand the relationship between the Fourier series and its complex number indication. (To see this, compare Figure 3-1 and Figure 3-3 with each other.)
|
Now, the k-th harmonic in this condition is represented as follows:
Figure 3-3 |
|
Xk* is a conjugate complex number of Xk. If the above is represented by complex coordinates with the real part (Re) plotted on the x-axis and the imaginary part (Im) on the y-axis, Xk* and Xk appear symmetrical to each other with respect to the Re-axis, as shown in Figure 3-3.
Since Figure 3-3 can be considered in the same way as was Figure 2-9 in Section 2-6 of the previous report, the following Equation 3-11 can be established:
|
Xk here is called a Fourier spectrum, 1/2ak the real part (Re) of the Fourier spectrum, and 1/2bk the imaginary part of the Fourier spectrum (Im). Moreover, |Xk|2 is termed a power spectrum. Incidentally, the Fourier spectrum in an FFT analyzer indicates ak and bk, and the power spectrum shows 4|Xk|2. This is because it is convenient to represent these terms with the rn, an, and bn used in Figure 3-1.
3-3 Fourier Transform
Since Equation 3-9a is a Fourier series, it represents a continuous, periodic time-dependent waveform. Substituting Equation 3-9b into this equation yields Equation 3-12 below. (For simplicity of calculation, the 0 to T section of the waveform was replaced with -2/T to 2/T.)
|
(Equation 3-12) |
Let us consider here extending period T to -![]() to +
to +![]() , so that waveforms without periodicity can also be handled. If, in Equation 3-12, we adopt for df a very small frequency ultimately reached as a result of enlarging T in 1/T, we have:
, so that waveforms without periodicity can also be handled. If, in Equation 3-12, we adopt for df a very small frequency ultimately reached as a result of enlarging T in 1/T, we have:
|
Substituting X(f) for the part in {} in the equation above, we obtain the following equations:
|
|
Equation 3-14 represents a Fourier transform and Equation 3-15, an inverse Fourier transform. Although 1/T disappears in Equation 3-14, the Fourier transform, it can be regarded to have moved to the inverse transform side of Equation 3-15. In this way, it can be understood that the pair of Fourier transform and inverse transform corresponds to the pair of Fourier expansion and series handled in Equations 3-9 above. However, be careful not to confuse Equations 3-14 and 3-15 with each other, as the two are very much alike.
X(f) represents the frequency domain and x(t), the time domain
While the spectrum was shown in the form of discontinuous harmonics in the Fourier series, it appears as a spectrum of continuous frequency in the Fourier transform, where the periodicity is expanded infinitely, causing the basic frequency f0(=1/T) to take on a very small value.
Now, let us consider the Fourier transform of x(t)=1.
We cut a certain time portion T out of an infinitely continuing value of 1 and we regard the rest as zero (0). Let us try to make a Fourier transform on this assumption.
Figure 3-4 illustrates two cases, T = 1 and T = 5. The conjecture is shown in Figure 3-4a, but it differs substantially from Figure 3-4b. However, if T is made larger, the waveform becomes narrower in width and the amplitude value also increases, creating a waveform closer to that in Figure 3-4a. This difference arises because we simply assumed the invisible portion as 0, and a larger T shows the characteristic of the whole waveform more clearly as a matter of course. As can be gathered, if we select a longer time T for which a waveform is cut out (called "time resolution") in a Fourier transform, the frequency resolution (= 1/T) will become higher, allowing us to view a more detailed spectrum. Conversely, if the time for which a waveform is cut out is set to be short (i.e., time base resolution is high), the frequency resolution will turn rough and indicate a spectrum only on a broad basis. In this way, the Fourier transform is possessed with a natural uncertainty, as it is called, between time resolution and frequency resolution. The FFT analyzer allows this time length T to be modified as a data length (number of samples), according to the intended application.
Figure 3-4 |
3-4 Discrete Fourier Transform
An FFT analyzer handles a time waveform x(t) as discontinuous data (discrete data) acquired at sampling interval h.
If the sampling value sequence of an N-number of finite data points sampled at sampling interval h is represented by x(n) (n = 0, ... N-1), the Fourier transform likewise holds true for that data. Since multiplying a time waveform x(n) by a given waveform e-j2pft and integrating one period of it provides the amplitude of the waveform, we apply this discrete data to the formula by using Equation 3-9b as a guide:
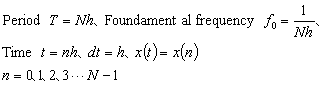 |
From the above, the Fourier transformation formula of the k-th harmonic is expressed as follows:
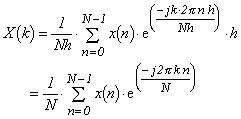 |
(Equation 3-16) |
Equation 3-16 is called a discrete Fourier transform (DFT). Moreover, the relation of Equation 3-11 also holds for this equation in the same way as for Equation 3-7b. Similarly, the inverse discrete Fourier transform (IDFT) is expressed by:
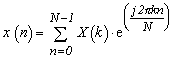 |
(Equation 3-17) |
Please refer to Figure 3-5 (click on it), where we have given a conceptual representation of Equation 3-16 for your reference.
So, to what extent can we calculate a harmonic k?
To know an original waveform, it is necessary to perform sampling at a frequency at least twice that of the waveform. This is called the sampling theorem.
Now, let us consider the case where an N-number of samples are taken for a waveform with period T. In this case, the sampling interval h and its frequency fs are expressed by:
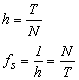 |
(Equation 3-18) |
Therefore, the frequency fm that can be analyzed using the sampling theorem is:
| (Equation 3-19) |
Namely, the analysis can be conducted up to the N/2-th harmonic.
If we sample a waveform with band limited from 0 to fm at fs and perform a DFT calculation, we obtain a spectrum of frequency - ![]() to +
to + ![]() Figure 3-6 illustrates a typical spectrum of frequencies from -fm to 4fm.
Figure 3-6 illustrates a typical spectrum of frequencies from -fm to 4fm.
Figure 3-6 |
As can be seen in the figure above, the spectrum obtained has the same value repeated, just like a paper folded at integer multiples of fm. A similar result to Figure 3-6 will also be obtained if we sample a waveform with band limited from fm to 2 fm at the same frequency fs and then perform the DFT calculation. This calculation will, however, provide us with the components of 0 to fm which do not exist in actuality. This is called an "aliasing" phenomenon (or "folding frequency") and a frequency fm in this condition is termed a Nyquist frequency. A simple look at just the 0 to fm range of the spectrum obtained will not enable you to tell whether the original waveform is from 0 to fm or from fm to 2 fm. For this reason, an FFT analyzer passes signals through a low-pass filter (dubbed an "aliasing filter") that previously limits them to fm and thus defines only signals below fm in order to meet the sampling theorem. Moreover, since frequencies up to fm, plus a, need to be considered in order to obtain frequencies that can fully be attenuated by the said low-pass filter, an FFT analyzer is designed to indicate spectra up to 1/1.28 of fm only (Figure 3-7).
Figure 3-7 |
Please note that Figure 3-8 shows the sampling theorem scrutinized from the standpoint of time waveforms, and Figures 3-9a and 3-9b (please click on them) exhibit the waveforms displayed by an FFT analyzer as the aliasing filter is turned on and off.
Figure 3-8 |
This discussion has assumed quite a complex and mathematical tone. We hope it has been clear to you up to this point.
At this time, we would like to review the Fourier series, Fourier transform, DFT, and sampling from the viewpoint of an FFT analyzer, with some imagery concepts mixed in. Part of this explanation will include quotations from the book "Introduction to Digital Signal Processing," written by Ken'ichi Kido.
Let's start by referring to Figure 3-10. Waveform "A" is a time waveform that is repeated infinitely with a band limited to less than a Nyquist frequency fm. "B" is the frequency spectrum obtained from "A", which is distributed over ± fm from its origin, and the part outside that range is zero (0). Then, assuming that spectrum X(f) of "B" is arranged infinitely on the frequency axis with period 2fx, the cases indicated below are likely:
Figure 3-10 |
When fx = fm, spectrum waveform of "C".
When fx < fm, spectrum waveform of "D".
When fx > fm, spectrum waveform of "E".
Here, the spectrum waveform of "E" represents the state in which the different spectra are overlapped on each other, causing aliasing to take place. The spectrum waveforms of "C" and "D" are identical to spectrum X(f) of x(t) in the range from -fm to +fm. Changing the angle of view, now let us consider sample train xn, where x(t) is sampled at 2fx. Spectrum xn in this condition is:
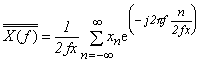 |
(Equation 3-20) |
This represents "C", "D" and "E" with an equation. In other words, if we sample a continuous waveform x(t) with band limited to fx at sampling frequency 2fx, seek spectrum X(f) from the data of its infinite sample train {xn}, and look at its frequency range from -fx to +fx, then we find that it is a frequency spectrum X(f) of x(t) in its own right ("C", "D").
Since application of inverse Fourier transform to X(f) yields x(t), the sampling value sequence at every 1/(2fx) has sufficient information to indicate a continuous waveform x(t). If the original waveform has a frequency that is higher than the sampling frequency, overlapped spectra (such as those shown in "E") will appear because of the aliasing effect, and the resultant spectrum will be different from X(f), making it impossible, therefore, to reproduce x(t).
The discussion up to this point has centered on the Fourier transform.
Next, suppose the waveform of "A" is repeated infinitely with period T like "F", such that the frequency spectrum resulting from the Fourier expansion of that waveform will present itself as a linear spectrum arranged on the frequency axis at interval 1/T. Since this waveform has its frequency component limited to less than fx, the spectrum will appear like "G", and the envelope of this linear spectrum will match the continuous spectrum of "B". If we assume here that the spectrum of "G" is identical to a spectrum "H" that is repeated infinitely with period 2fx, like "C" and "D", the time waveform obtained from applying an inverse Fourier transform to "H" will appear as a sampling value sequence that is repeated infinitely with period T, as shown in "I". That is, both the time waveform and the spectrum appear as a sampling value sequence repeated periodically and infinitely. These relationships are represented by DFT and IDFT of Equations 3-16 and 3-17. Since the following parts of Equations 3-16 and 3-17 are periodic functions that take the same values repetitively with a certain period, like the sine and cosine waveforms, it will be understood that DFT and IDFT represent "H" and "I" of the figure:
Furthermore, it will also be clear that they give sufficient information to the user, provided that the spectra of 0 to fx can be obtained correctly. Given below for reference purposes is an equation to restore a continuous waveform from a spectrum.
Sample train {xn} is expressed by:
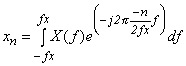 |
(Equation 3-21) |
And, the Fourier coefficient in the term of -n of its spectrum X(f) corresponds to xn. Moreover, a continuous original waveform x(t) can be obtained from sampling value sequence {xn} by the following equation (see Figure 3-11):
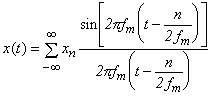 |
(Equation 3-22) |
Figure 3-11 |
Let's wrap up this explanation of Fourier series and Fourier transforms for now by giving a brief roundup of information on DFTs.
Summary
Suppose signal x(t) which is infinitely repeated with period T has its band limited to below a certain frequency, and that a discrete spectrum (linear spectrum) X(f) can be found performing DFT at every 1/T =1/Nh, based on a discrete sample train {xn} acquired from signals of period T in an N-number at constant interval h conforming to the sampling theorem. Likewise, a discrete sample train {xn} can be reproduced by performing an IDFT.