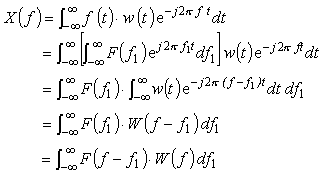7.FFTと時間窓(ウィンドウ)
ここまでの理論をベースに、FFT と窓関数について考えてみます。今、FFT アナライザーにより複雑な連続波形をサンプリングし、ある一部分 n = 1024 or 2048 点分のデータを切り取って、これを1周期 T とした領域を考えてみます。この周期 T の波形が無限に繰り返されていると仮定し、FFT の計算が行なわれます。この連続した波形は、切り取られる波形位置によって FFT の値が変わってきます。
この事を sin 波形で考えてみます。
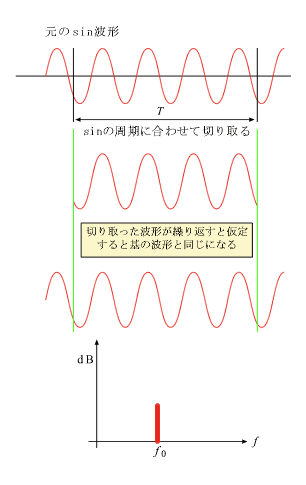
図 7-1 はちょうど sin 2π f0 波の周期に一致するように切り取られているため、仮定する波形も元の sin 波形と同じ連続した波形になり、そのスペクトルには周波数 f0 の成分しか現れません。
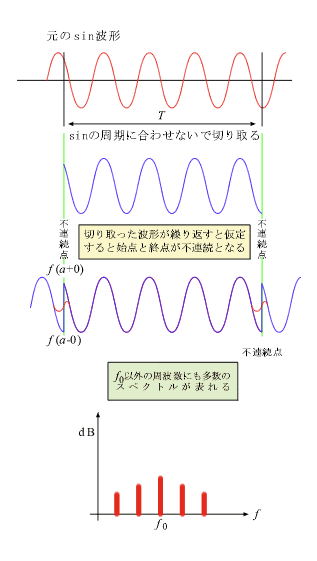
次に、その下の図 7-2 は sin 波形の周期に一致しないで切り取られた場合を示しています。この場合、仮定の波形は周期 T の点で f (a - 0) から f (a + 0) に急に変る不連続点を持った波形になります。
こうして短い時間で切り取られた波形は、sin 2π f0 の元波形ではなく、違う波形となってしまいます。そのためこの波形は図 7-2 のように f0 以外にも多数の周波数成分を持っていることが予想されます。
図 7-2 を、切り口を変えて見てみましょう。
n = 2048 点の有限サンプル列から有限近似スペクトルが求められます。この有限近似スペクトルを逆フーリエ変換した波形はどこまで元の波形を近似しているのでしょう。図 7-2 の切り取られた元の波形に対し、不連続であった始点と終点がどの点でつながる(収束する)かと言うと、f (a - 0) と f (a + 0) の中点で点線のように滑らかにつながることになります。これはフーリエ変換・逆変換の積分式に対し、積分の性質である次の定理によります。
| 『ある関数 f (t) が a で不連続点を持つとき、不連続点に対し左側から接近した時に収束する値を f (a - 0)、右側から接近したとき収束する値を f (a + 0) とすると、積分値はその平均値に収束する。』 |
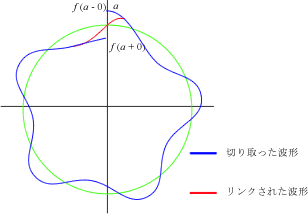
実線、点線を1周期を円にして描き直すと図 7-3 のようになり、フーリエ逆変換では周期 T で1回転し、その軌跡が同じ軌跡になります。
|
図7-1 |
|
図7-2 |
|
図7-3 |
この様に同じ sin 2π f0t の sin 波形の FFT であるのに切り取り方によって結果が違うと困ってしまいます。
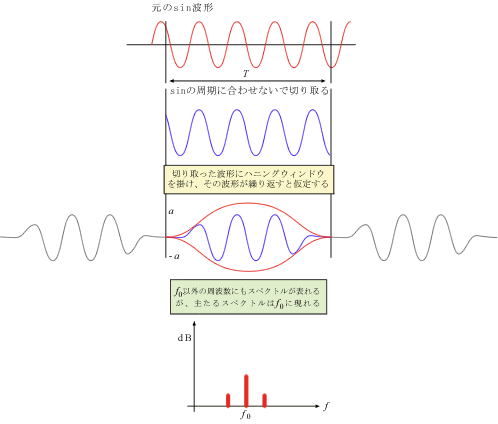
FFT アナライザーでは、周期 T は固定であり、また周期が不明の信号を FFT するのですから図 7-1 のように常にうまく切り取ることは不可能です。そのため、図 7-2 のように始点と終点が不連続にならない工夫が必要となります。工夫として、「切り取った波形の始端と終端とを徐々に小さくしていき始点・終点がゼロになるような重み関数を掛けてやる」とどうでしょう。このような関数の一つが、ハニングウィンドウと呼ばれる関数ですが、この重み関数を、切り取った sin 波形にかけてやると、図 7-4 のように、繰り返される連続波形が仮定されそのスペクトルも周波数 f0 を主にして現れます。ハニングウィンドウを掛けることにより切り取る位置による影響を小さくすることが出来ます。
|
図7-4 |
このような理由による重み関数を時間窓(time window、時間窓関数)と言います。
それでは次に、城戸健一著「デジタル信号処理入門」より引用しながら良く使用される時間窓をみていきましょう。
実際に使われている時間窓関数 w (t) を例に取りその特徴を見ていきます。それには、ある時間窓関数 w (t) を時間軸波形 x (t) にかけたとき、元の x (t) のスペクトルがどのように変化するか考えます。
f (t) ←→ F (f)、 w (t) ←→ W (f) とすると
f (t) と w (t) の積 x (t) のフーリエ変換 X (f) は:
|
|
(式7-1) |
この式 7-1 は、f (t)・w (t) 2つの関数のかけ算のフーリエ変換が周波数領域ではそれぞれの関数 F (f) * W (f) の畳み込み積分になっていることを表しています。周波数領域で W (f) が f = 0 で1、それ以外は 0 と言う理想的な窓関数は時間領域では t が −∞ 〜 +∞ で1の値を取る窓関数となり、実用的ではありません。FFT が有限長サンプル数と言うことから、使用する窓関数も有限長で、そのスペクトルは周波数の広がりが狭いものが望まれます。