O-Solution 時間周波数解析機能 OS-0527
FFT解析では捉えることが難しかった過渡現象を評価する事ができます。特徴量(周波数)を周波数分解能を維持したまま、周波数成分の時間変化を鮮明に表示する事がでます。短時間フーリエ変換とウェーブレット変換を搭載しています。
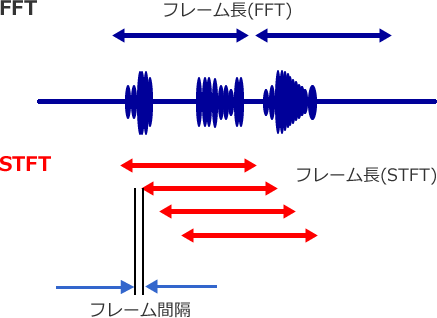
短時間フーリエ変換 STFT (Short Time Fourier Transform)
ユーザ任意のポイント(フレーム長および間隔)でフーリエ変換を実行できます。よってユーザが任意に切り出し時間長を設定できるので、非常に短時間のスペクトル変化を観察するときに有効な手法です。
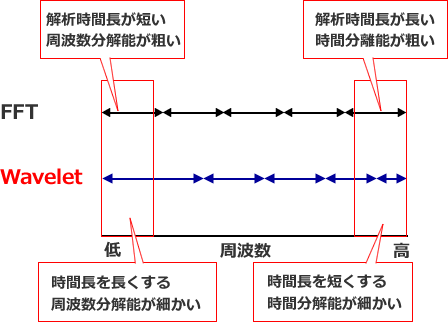
ウェーブレット変換 (Wavelet transform)
突発的なまたは非定常的な音響や振動などの複雑な波形の時間的変動と空間的推移を同時に解析することを可能とした解析手法です。この手法は、周波数によって解析時間長を変えています。時間・周波数のバランスが良いので、解析結果の全体を捉えるのに有効です。
| 項目 | 短時間フーリエ変換 | ウェーブレット変換 |
|---|---|---|
| 時間分解能 | 一定 | 高周波数:高い 低周波数:低い |
| 周波数分解能 | 一定 | 高周波数:低い 低周波数:高い |
| 特長 | FFT演算の拡張である。 安定した結果を得る事ができる。 |
時間分解能、周波分解能のバランスが良い |
| 弱点 | 時間分解能、周波分解能を高くすると、 計算時間、データ量が大きくなる |
おおよその周波数しか分からない。 |
時間周波数解析事例 衝撃信号の解析
過渡的な振動波形を解析したい。通常のFFT分析では時間分解能が粗く詳細な解析ができない。短時間フーリエ変変換を用いている事で高い周波数分解能と時間分解能の結果を得る事ができる。
| 型名 | 品名 | 数量 |
|---|---|---|
| OS-5100 | プラットフォーム | 1 |
| OS-0522 | FFT解析機能 | 1 |
| OS-0527 | 時間周波数解析機能 | 1 |
|
※音を収録する機器(高機能騒音計、FFTアナライザーなど)が必要です |
||
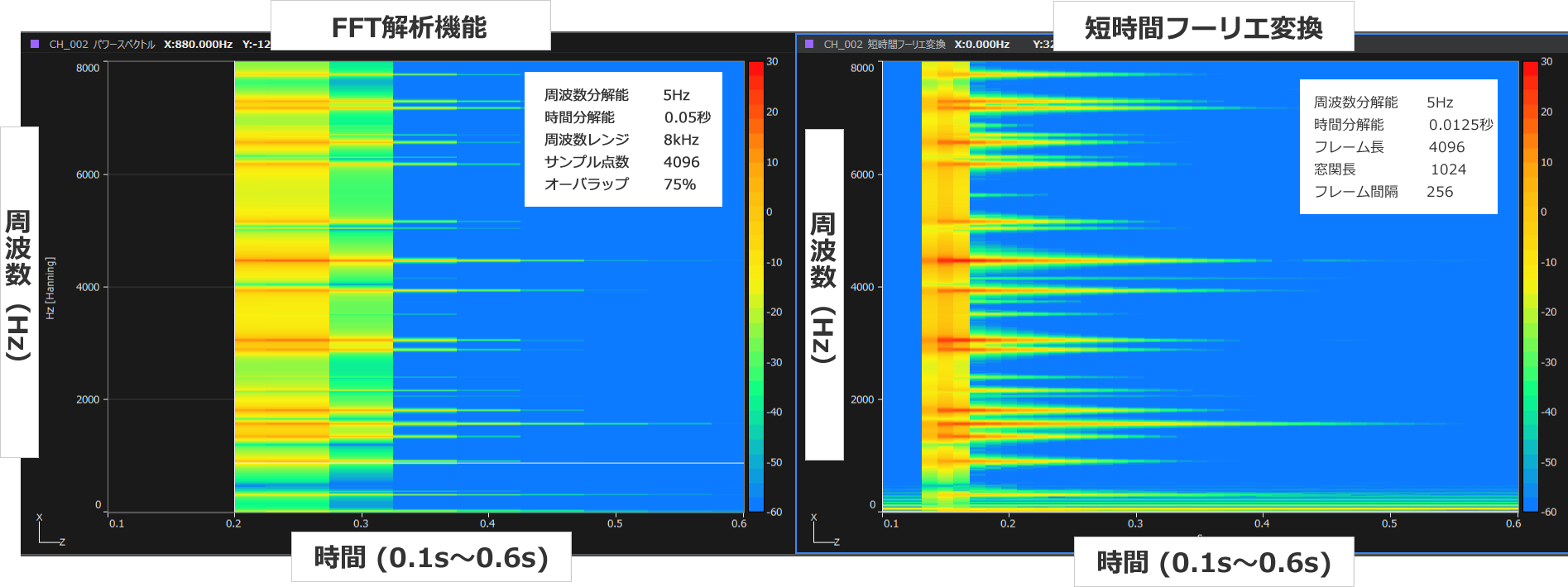
時間周波数解析事例 ゴルフクラブインパクト音の解析例
短時間に周波数が変化する、ゴルフクラブのインパクト音を解析した事例です。
対象信号の時間長が短いため、FFT解析では時間方向の細かいスペクトル変化はぼやけてしまいます(左図)。
STFTを用いれば、同じフレーム長であっても、フレーム間隔および窓関数長をユーザが任意に設定できるため、
周波数分解能を維持したまま、短時間に変化する周波数成分の時間変化を鮮明に表示することが可能になります(右図)。
| 型名 | 品名 | 数量 |
|---|---|---|
| OS-5100 | プラットフォーム | 1 |
| OS-0522 | FFT解析機能 | 1 |
| OS-0527 | 時間周波数解析機能 | 1 |
|
※音を収録する機器(高機能騒音計、FFTアナライザーなど)が必要です |
||

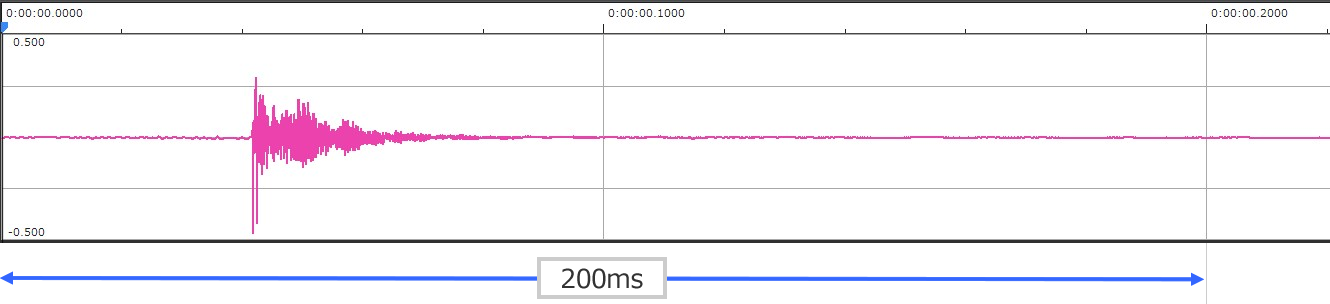
ゴルフグラフのインパクト音 時間波形
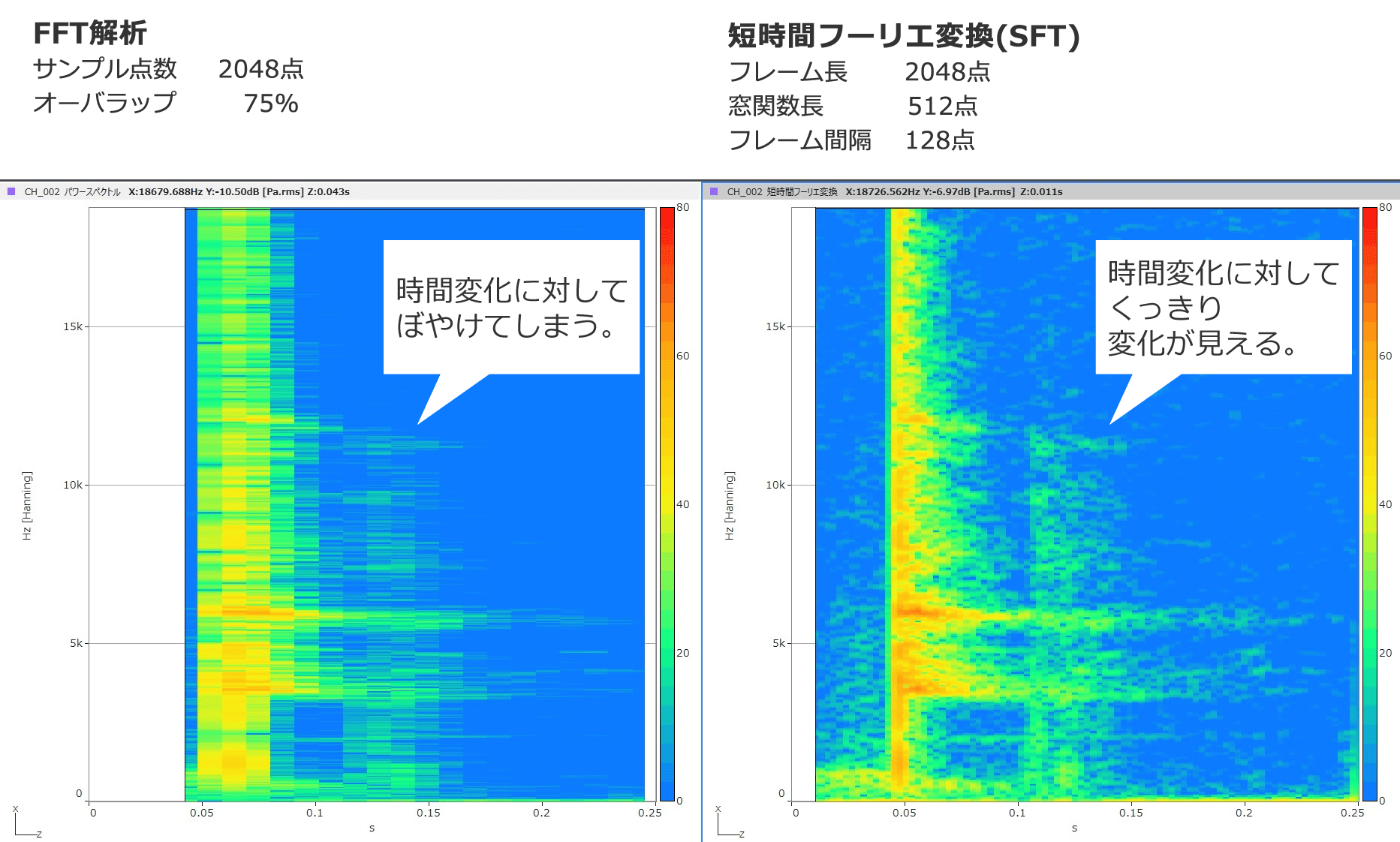
時間周波数解析事例 機械工作音の解析
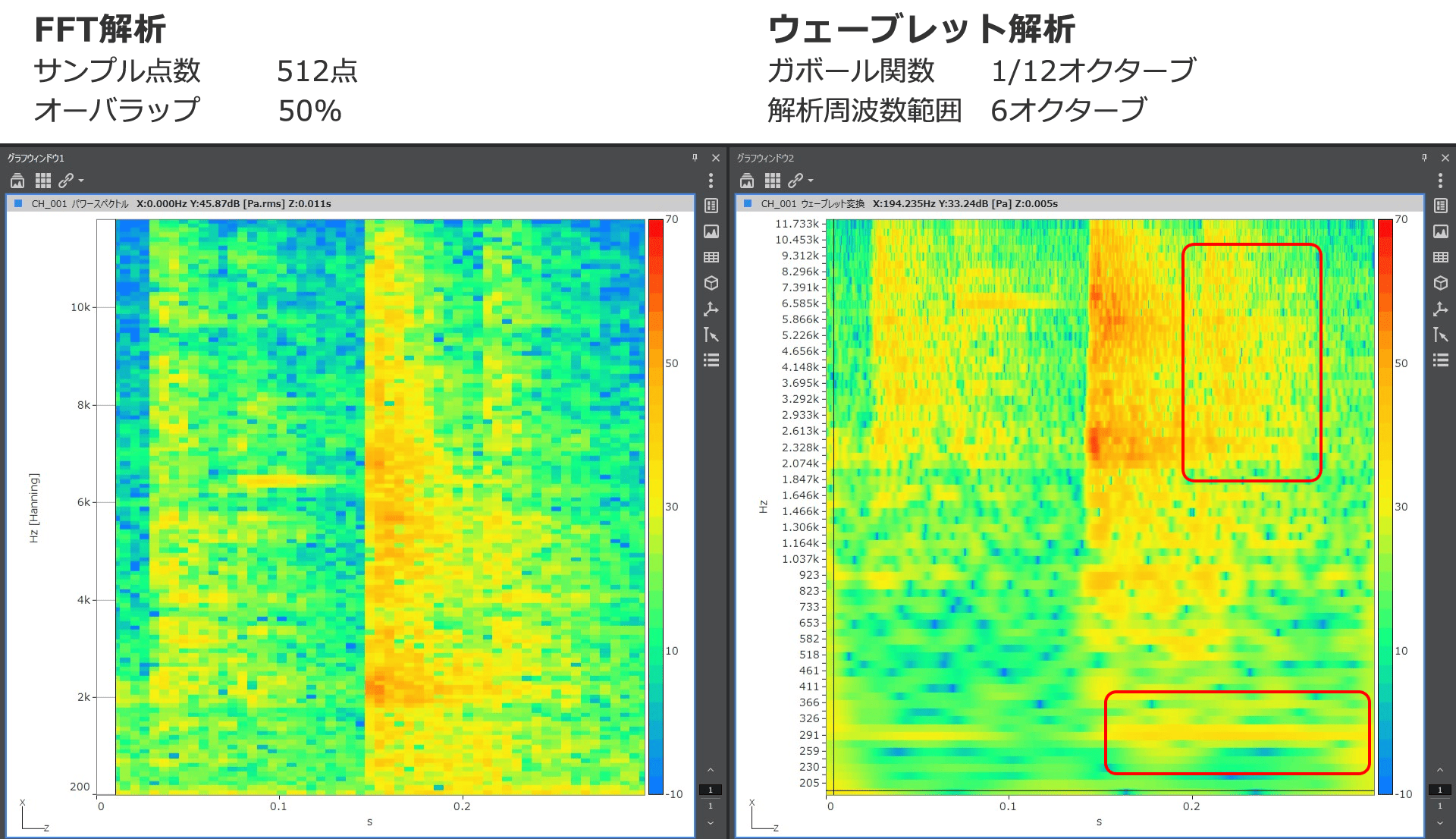
機械工作音に含まれる、非常に短い異音を解析した事例です。
異音の周波数成分が広範囲に渡るため、低い周波数成分の分解能を得るためにFFT解析では
フレーム長を十分大きく取る必要があります。
しかし、発生する異音の時間長が非常に短いため、フレーム長をできるだけ短くする必要もあり、
周波数分解能、時間分解能の両方とも十分に得られません(左図)。
この例では、FFT解析では見落としてしまう赤丸で囲った部分の成分(低い周波数成分)が見えてきます(右図)。
このようにウェーブレット変換は、(周波数分解能が十分な)高い周波数ほど周波数分解能を落として時間分解能を上げ、(時間変化が緩やかな)低い周波数分ほど時間分解を落として周波数分解能を高く解析します。
つまり、その分析手法は、音響分析によく使う1/Nオクターブバンド分析と同様な定比型フィルタバンクによる分析です。
| 型名 | 品名 | 数量 |
|---|---|---|
| OS-5100 | プラットフォーム | 1 |
| OS-0522 | FFT解析機能 | 1 |
| OS-0527 | 時間周波数解析機能 | 1 |
|
※音を収録する機器(高機能騒音計、FFTアナライザーなど)が必要です |
||