|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
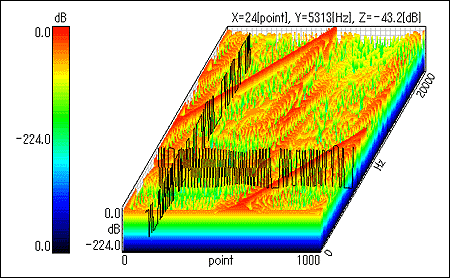
■ウィグナー分布ウィグナー分布 (Wigner distribution) とは、突発的または非定常的な音響や振動などの複雑な波形の、時間的変動と空間的推移を同時に解析することを可能とした解析手法です。 ウィグナー分布は、1932 年量子力学の分野において E.Wigner によって提唱され、その後 T.Classen や W.Mecklenbraker らによって音響分析に応用されてから、非定常信号の分析手段として注目されはじめました。 エネルギーの次元を持つウィグナー分布は、時間と周波数の分解能がともに最も高いので、過渡信号の特徴を従来の手法に比べよりよく捉えることができます。 ただし、負のエネルギーおよびクロス項が現れることが多く、その解釈には専門性が必要となります。 ウィグナー分布関数がもつ非定常信号の時間・周波数分布を利用することにより、衝撃音や異常音、音響機器の過渡特性などの解析に有効なツールになることが予想されています。
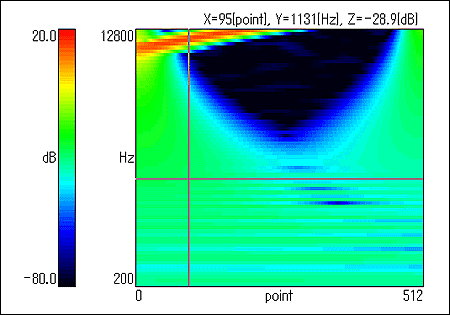
■ウェーブレット変換ウェーブレット変換 (Wavelet transform) とは、突発的または非定常的な音響や振動などの複雑な波形の、時間的変動と空間的推移を同時に解析することを可能とした、現在も発達を続けている新しい解析手法です。 当初ウェーブレット変換による解析は、石油探査技師により人工地震波解析の道具として最初に導入されて以来、物理学者や数学者、工学者らの努力により、数学的基礎付けからさまざまな分野への応用が試みられています。 ウェーブレット変換は、その名ウェーブレット (局在する小さな波) の示すとおり、時間的にも周波数的にも (実用上は) 局在した一つの関数を用意し、これにスケール変換とシフト変換を作用させて得られる関数の組を基底関数として用いる変換です。 低周波 (ゆっくりとした変動) では長い時間データを、また高周波 (はやい変動) では短い時間データをそれぞれ使用するという自然な分析手法であるため、さまざまな過渡現象の解析手段として注目を浴びている手法です。なお、ウェーブレット変換結果の絶対 2 乗値の分布をスケーログラムと呼びます。 DS-0230 時間-周波数解析ソフトウェアのウェーブレット変換は、時間-周波数の平面上に信号のスペクトルを、2 次元のカラーイメージまたは 3 次元のカラーイメージで、それぞれ表示させることができます。
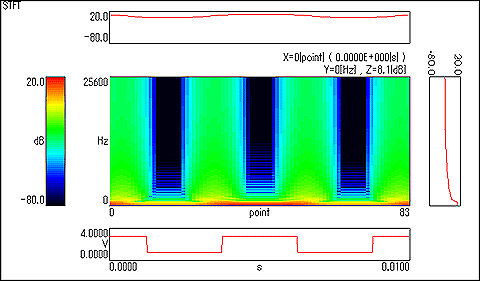
■STFT非定常信号の周波数成分の時間変化を捉えるために、短時間毎に信号を切り出しフーリエ変換したものが STFT (Short Time Fourier Transform) です。 短時間フーリエ変換は、非定常信号の解析としては最も単純で扱いやすい手法です。 一般的に FFT では、時間変動に対する精度 (時間分解能) を良くするためには取り出す時間長を短くする必要があり、それに応じて周波数に対する精度 (周波数分解能) は悪くなります。 そこで、STFTでは、切り出し時間窓とフーリエ変換の長さを別に設定することにより必要な周波数分解能を保ったまま時間分解能を良くする工夫がなされています。 なお、短時間フーリエ変換結果の絶対 2 乗値の分布を、スペクトログラムといいます。
|