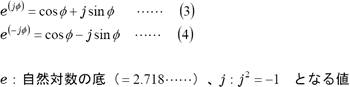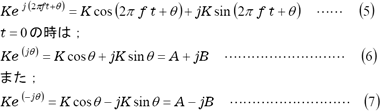メールマガジンバックナンバー & 計測コラム

メールマガジン66号補足

■円運動をしている球体の影の時間経過

　

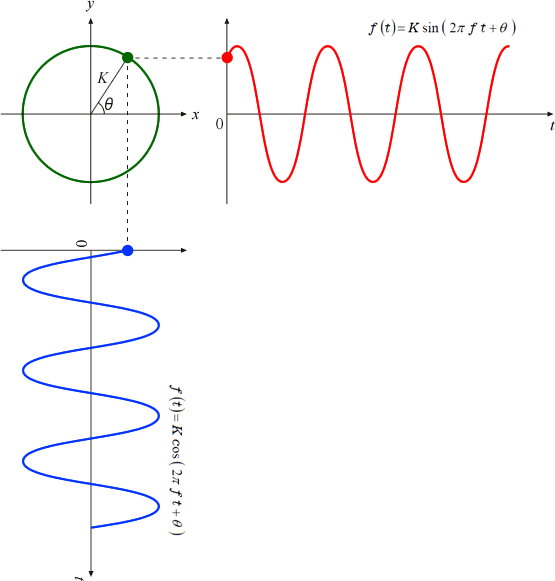
図１

■初期位相のあるcos波

　

　

図２

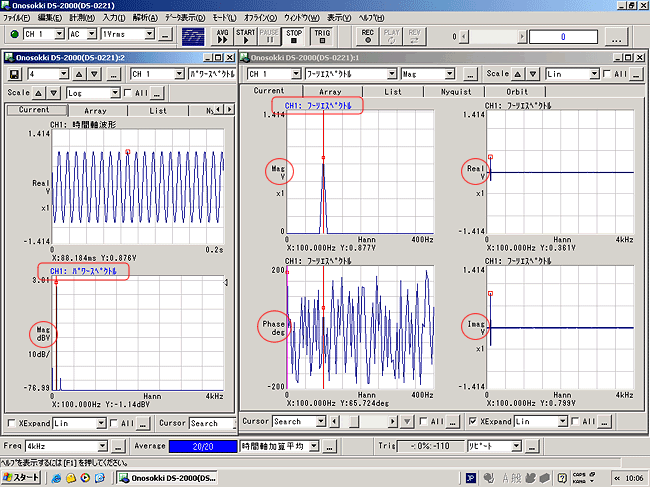
図３

任意の振幅で100Hzのcos波を入力し適当なレベルでトリガーをかけて測定しました。cos波なのでわかりやすくするため片振幅（0-P）表示としています。また、位相のX軸は拡大しみやすくしています。

測定データを読み取ると次のようになります。

このデータから、今回の話に沿ってデータの関連をみていきますと、次のようになります。

FFT（高速フーリエ変換）で求まるのは図３右上、右下のデータA、Bです。

A（実部）＝0.350V、B（虚部）=0.804V

これより入力波形の振幅K、初期位相θは；

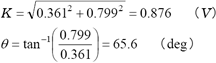
この値は図３の中上、中下データに表示されています。TIME波形は；

であることになります。パワースペクトルは；

　

＜補足説明＞　

実部、虚部について

実部、虚部は複素関数にでてくる用語です。オイラーの公式は；

オイラーの公式は指数関数も包含しているため複素指数関数といわれます。複素指数関数はcosとsinが複素数を表すｊで合体されて、cosとsinを同時に扱えて便利な記号です。ｊのつかない数Aは【実数】、ｊの付いた数jBは【虚数】といいます。また、ｊのつかない項Aを【実部】、ｊの付いた項Bを【虚部】といいます。FFTアナライザーの場合、実部はcosの項、虚部はsinの項と理解してしまっていいでしょう。

さて、式(2)に相当する複素関数式は；

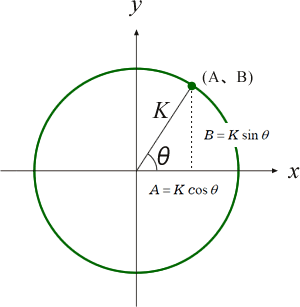
式(6)、式(7)は複素平面（ガウス平面：X軸は実部、Y軸は虚部）では実に対して対称の関係になり【共役複素数】といわれています。 下図４は式(6)(7)を複素平面（ガウス平面）で表わしたものです

　

　

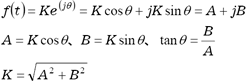
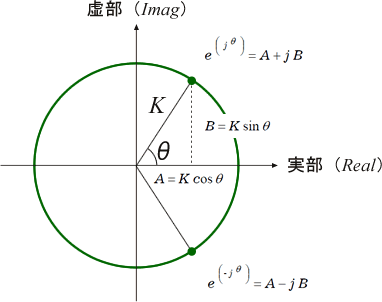
図４

　

式(2)と式(6)(7)を比べてみましょう。極性±を無視するとどちらもA、B、K、θの関係は同じ関係にあることがわかります。FFT（高速フーリエ変換）の演算は複素数の計算になりますが、cosの項A、sinの項Bを求めていると思えば、FFTアナライザーを理解したようなものです。