メールマガジンバックナンバー & 計測コラム
メールマガジンバックナンバー
メールマガジン58号補足
■ 図5:半値幅法とQ 値、減衰比 ζ
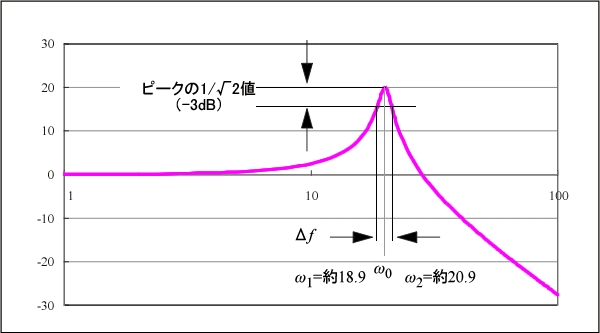
Q=1/(2ζ)=ω0/(ω2-ω1)
ω2、ω1を計算値から探すと、ω2=約20.9、ω1=約18.9
Δω=ω2−ω1= 約20.9 - 約18.9
ωo=20
Q=ωo/Δω=1/(2ζ)=20÷2=10
ζ=0.05 と、半値幅法の確認ができました。
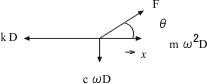
■ 図6:外力 F、慣性力 mω2D、減衰力 cωD、バネ力のつりあい
ω<ωoの場合
ωが小さい時は慣性力mω2Dは小さく、外力Fと慣性力でバネkDに対抗する形になる
 |
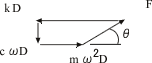 |
ω=ωoの場合
慣性力は外力より90度遅れ、慣性力とバネ力が対抗し、外力と減衰力が対抗する関係になる。xは最大(Dが最大)になり、慣性力、バネ力も最大となる。また、速度も最高になり減衰力も最大となる。
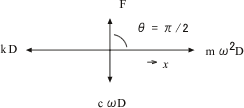 |
|
ω>ωoの場合
ωが大きくなると慣性力は外力より次第に180度遅れてくる。Dはωが大きくなると小さくなり、kD、cωDは小さい。慣性力はω2に比例するが、一定の大きさFにつりあうため、
x(D)は急減する。
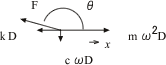 |
|