メールマガジンバックナンバー & 計測コラム
メールマガジンバックナンバー
メールマガジン51号補足
前号の手順に従い、フィールドバランシングキットを使ったバランシング測定とその修正を、FFT アナライザーを使って実験してみました。今回はこのデータを使いフィールドバランスのベクトルの作図からバランス修正の手順について話しをすすめます。三角関数を使った計算方法も参考ください。
(1)実験システムの構成
実験の構成は図1のようになります。
|
図1 |
(2)運転条件
ロータの回転数は 2480 r/min、この時のアンバランスを修正することとします。 ロータには、修正重りが取りつけられるように 22.5 度毎にねじが切ってあります。
実験のため、アンバランス用にロータの位置 0 度にねじを取りつけました。この様子を図 2 に示します。
|
図2 |
(3)測定条件
ロータの回転数 2480 r/minより、アンバランスの周波数 f(回転1次の周波数)は
f=2480÷60=41.3 (Hz)
FFTアナライザーの設定で、仮に周波数レンジを 1 kHz、サンプル数を 2048 点にすると
サンプル周波数 sf、周波数分解能 ⊿f は
sf=1000×2.56 (Hz)
⊿f=1000÷800=1.25 (Hz)位相分解能⊿θは
⊿θ=360(度)÷(1回転のサンプル数)=360÷(1000×2.56÷41.3)≒6 (度)
バランス修正の精度を上げるためには位相分解能は 5 度以内を目安にとります。この目安からすると周波数レンジは 2 kHz になりますが、修正重りの取りつけ角度が 22.5 度毎なので 1 kHz レンジとしました。
(4)トリガ
基準信号は HT-5200 型回転計を利用し、反射マークを検出したパルス出力を CF-3600 型 FFT アナライザーの ch 1 に入力しました。
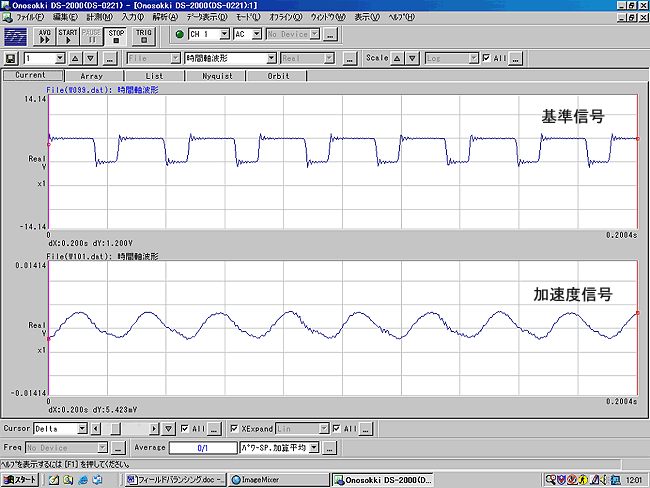
Ch 1 の波形を見ながらトリガレベルを調整し、ポジションは 0 とします。トリガをかけて取りこまれた加速度ピックアップの波形は図 3 のようになります。 見やすくするため X 軸を拡大して表示しています。
|
図3 |
フィールドバランシングソフトを使う場合は、基準信号は外部サンプル端子へ入力し、次数分析を行い、その回転 1 次成分に注目しますが、この実験では ch 1 の基準信号でトリガをかけ ch 2 の加速度波形のフーリエスペククトルから振幅、位相を測定することとします。 なお、トリガをかけることは基準位置を決めるために必要な操作です。
(5)データの平均
今回の実験では加速度の波形がきれいですので、平均化しなくてもアンバランス測定には問題はありませんが、いろいろな要素の振動波形が混在してノイズがのった波形では測定にばらつきが発生します。このようなノイズ除去のため時間軸平均をおこないます。時間軸平均は、波形を重ね書きし、その平均をするような処理になります。回転に同期したアンバランスの信号は、トリガ機能で測定ごとに波形が重なりあいますが、ノイズ成分は回転に非同期なため重なることが無く、そのため平均すると除去されます。
平均回数は波形が安定することを目安に決めます。今回は 50 回に取りました。
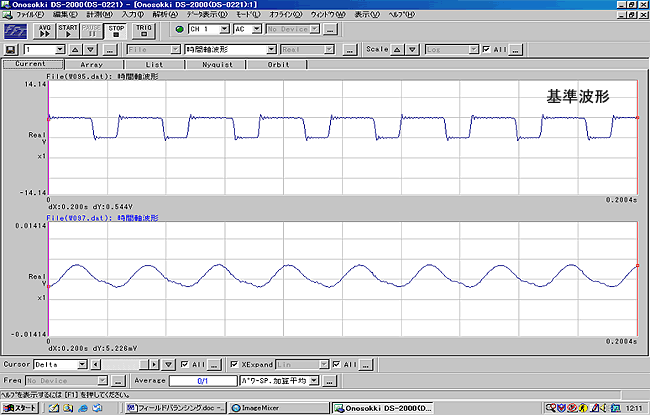
時間軸平均した波形を図 4 に示します。図 3 と同様 X 軸を拡大して表示しています。
|
図4 時間軸の平均 |
(6)イニシャル試験
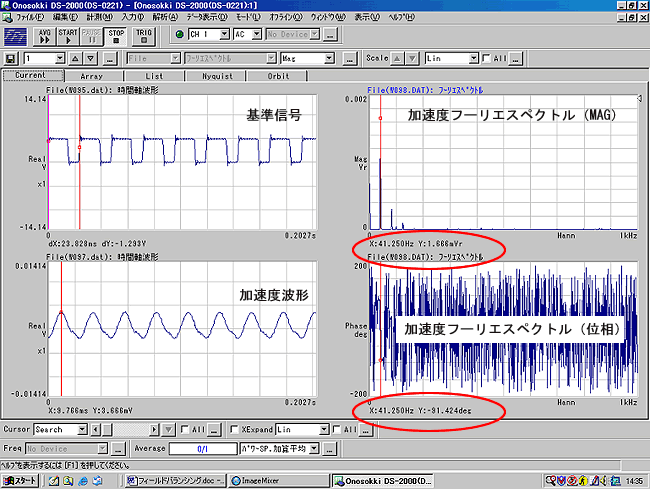
現状のアンバランスを測定します。2480 r/min で運転し、時間軸平均したパワースペクトルと位相スペクトルを図 5 に示します。
|
図5 |
この測定から回転 1 次の周波数 41.25 Hzの加速度電圧 1.666 mV、位相差−91 度が読み取れます。 位相差は cos(2π×41.25 Hz)の基準波形より 91 度遅れた波形を表します。特に極性と回転方向の関係が重要で、位相差が−極性の場合は、回転方向とは逆の方向にずれていること(遅れ)を、+の極性の場合は回転方向と同じ方向にずれていること(進み)を意味します。 また、振幅表示は一般的には変位としますが、加速度ピックアップの感度から電圧を加速度に変換し、さらに 2πf の自乗で除算すれば変位に換算ができること、修正重りは比例計算でできることから、ここでは変位への換算表示は省略します。
(7)試し重り
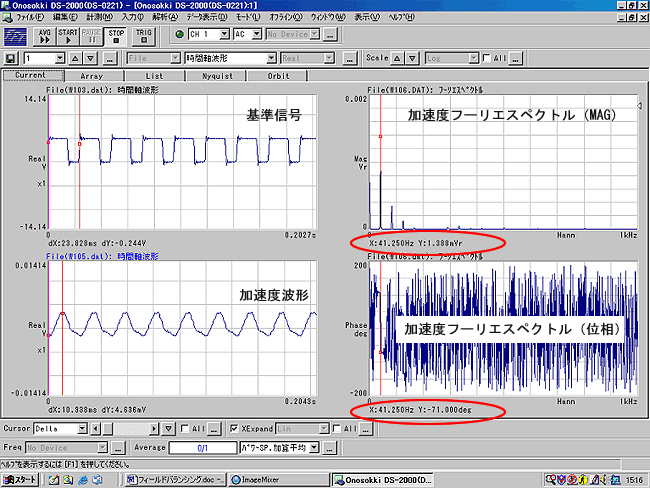
試し重り 2 g を軸の基準位置から 90 度の位置に取りつけました。(6)と同じ運転条件で測定した結果を図 6 に示します。
|
図6 |
この測定から回転 1 次の周波数 41.25 Hz の加速度電圧 1.388 mV、位相差 −70 度が読み取れます。
(8)ベクトル作図
測定データをまとめると表1になります。
| イニシャル試験 |
試し重り試験 |
||
| アンバランス量 | 1.666 (mV) | 1.388 (mV) | 試し重り2gを、ロータの位置90度に取り付け |
| 位相差 | -91(度) | -71 (度) | |
| X座標 | -0.0278 | 0.453 | |
| Y座標 | -1.670 | -1.314 | |
表1
表より X、Y 座標におきかえると、
イニシャル試験(
)
X: 1.666cos(-91)=-0.0278
Y: 1.666sin(-91)=-1.670試し重り試験(
)
X: 1.338cos(-71)=0.453
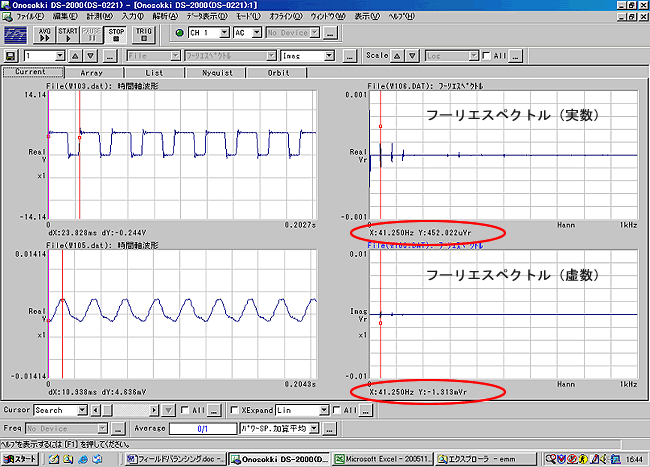
Y: 1.338sin(-71)=-1.314余談ですが、上記の X、Y の計算はフーリエスペクトルの実数、虚数と同じで、図 7 のように測定表示を実数、虚数にすると読み取ることができます。
|
図7 |
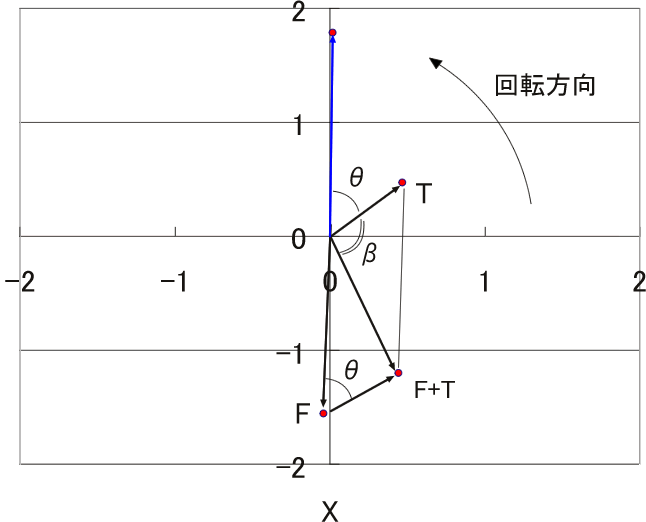
これよりベクトルとして作図をしたものを図 8 に示します。
|
図8 |
図 8 では位相差の極性そのままにして描きましたので、実際の回転方向と逆になっています。 回転方向はロータの右側から見るか、左側から見るかで回転方向は逆になりますから、注意しましょう。
さて、図 8 のように作図をすると T、θ はメジャーと分度器で測定できますが、次のように計算で求めることができます。
|
|
より、それぞれ X 軸と Y 軸の成分に分けて計算すると
は
X: 0.453−(-0.0278)=0.481
Y:(-1.314)−(-1.670)=0.356試し重りと修正位置の角度 θ は、
、
、
は平行四辺形なので、平行四辺形の内角の和は 360 度より
θ=(360−2β)÷2={360−2×(36.5+91)}÷2=52.5 (度)
修正重りの大きさWuは
Wu=(試し重りの重さ)×(
の大きさ)÷(
の大きさ)=2×1.670÷0.598=5.58 (g)
よって、試し重り 2 g を外し、修正重り 5.58 g を、修正重りをつけた位置から回転方向へ 52 度 の位置、軸の角度位置では 90 + 52 = 142 度の位置へ取りつけることでアンバランスの修正を行うことができます。
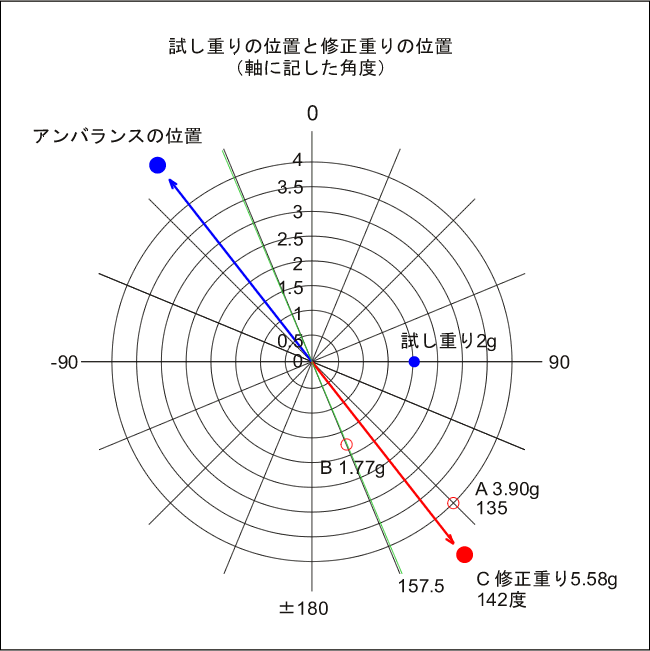
ここで問題が発生しました。図 2 のように 142 度の位置には修正重りを取り付けることができません。取り付け位置は 135 度か 157.5 度になります。試しに 135 度の位置に 5.58 g をつけて測定しようとしたら、振動が大きくなり危険で運転できませんでした。 アンバランス、試し重り、修正重りの位置関係を図9に示します。
|
図9 |
(9)分力の計算
5.58 g、142 度を 135 度と157.5 度に分力として計算してみましょう。
より
X: 5.58cos142=Bcos135+Ccos157.5
Y: 5.58sin142=Bcos135+Ccos157.5この連立方程式を解いて
B=3.90 (g)
C=1.78 (g)軸の位置で 135 度のところに 3.9 g、さらに 157.5 度のところに 1.77 g の修正重りをつけると、142 度に 5.58 g をつけたことと同じになります。図 9 にこの重りの位置A、Bを書いていますので参照ください。
(10)確認試験
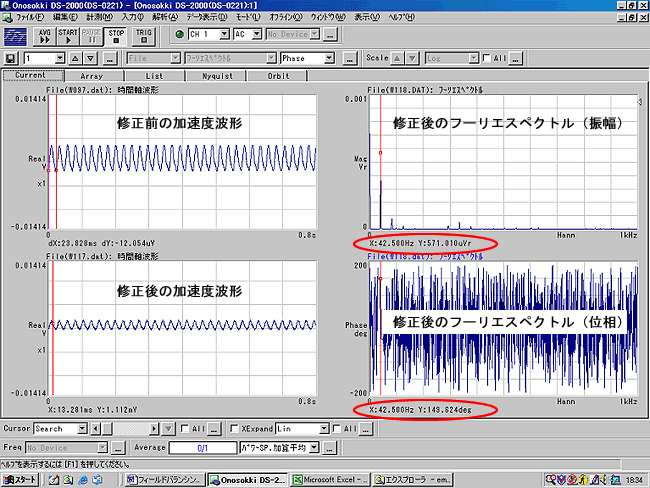
3.9 g の重りがありませんでしたので代わりに 3.5 g の修正重りを 135 度の位置につけて、確認試験を行いました。そのデータを図 10 に示します。なお、回転数が 2540 で試験したので回転 1 次の周波数は 42.5 Hz になります。
|
図10 |
今回は手元に適切な重りが無く、修正重りを 135 度の1箇所にしかつけませんでしたが、振幅は 0.571 mV、位相差 +149 になり、振動の低減効果が確認できました。アンバランスの位置も移動しています。ファン等修正重りの取り付け位置が決まっている場合、このような方法で分力計算し、2個所に適切な修正重りをつけてバランス修正を行います。 表 2 は以上の測定、計算した数値をまとめました。
|
イニシャル試験 |
試し重り試験 |
試し重り |
|
| アンバランス量 | 1.666 (mV) | 1.388 (mV) | 0.598(mV) |
| 位相差 | −91度 | −71 度 | +36.5度 |
| X座標 | −0.0278 | +0.453 | +0.481 |
| Y座標 | −1.670 | −1.314 | +0.356 |
| 重りの取り付け |
- |
試し重り2gを、ロータの90度位置に取り付ける。 |
修正重りを5.58gを142度に取り付けるか、代わりに3.9gを135度、1.77gを157.5度の2ヶ所に取り付ける。 |
表2
DS-0227バランシングソフトでは図 9 のような図示を自動で行ってくれて便利になっています。