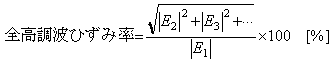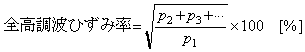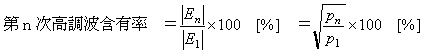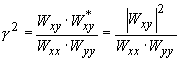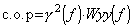FFT解析に関する 基礎用語集

機械などの構造物の動的特性の測定では、通常、構造物にハンマーでインパルスを加えて得られるインパルス応答を、FFTで処理して系の伝達関数を求めている。
しかし、FFTを用いた伝達関数は、有限の等間隔周波数分解能をもつ離散値データであるため、振幅曲線が急激に変化する固有振動数付近では測定点が非常に少ない。
そのため、これから求めたナイキスト線図は理想的な円軌跡とはならないので、正しいピーク値、固有振動数などのモーダル・パラメータを得るためには、この等間隔データ間を補間しながら計算する、曲線あてはめ（カーブ・フィット）が必要である。

カーブ・フィッティングと呼ばれる手法は、伝達関数の解析式を想定し、この式中の固有振動数、減衰比、振動モードなどのモーダル・パラメータを適当な値にすることにより、実測された伝達関数とモデルの伝達関数をできるだけ近似させるようにするものである。
これは、モーダル解析において、構造物の動的応答を理論的に決定づけるものである。

実際のカーブ・フィッティングでは、まず測定して得られた離散系の複素伝達関数の実数部と虚数部を用いて、複数個の点をナイキスト線上にプロットする。
次に、これらの点との誤差が最小になるような、理論上のナイキスト線図を算出し、このナイキスト線図から改めて伝達関数を計算して求め、測定した伝達関数にこれをフィットする。

測定された伝達関数のカーブ・フィッティングには、主として2つの方法が用いられる。
各振動モードのピークが離れていて、相互に影響を及ぼさない場合には、1自由度系のカーブ・フィット（SDOF:Single-Degree-of-Freedom curve fit）が使われる。
一方、隣接する振動モードの特性が互いに重なり合った場合には、多数の振動モードの影響を考慮する必要があり、伝達関数を解析的に表現している多数のモーダル・パラメータを、測定された伝達関数に同時に適合させる計算アルゴリズムが要求される。
この方法は、多自由度系カーブ・フィット（MDOF:Multi-Degree-of-Freedom curve fit）と呼ばれている。

FFTを行うための時間データは　２のべき乗の点数になります。この点数を小野測器のFFTアナライザーでは、サンプル点数（フレーム長）と呼んでいます。

64、128、256、512、1024、2048、4096 の時間データをFFT して25、50、100、200、400、800、1600 点の周波数データが得られます。

このように、周波数分解能はFFT のサンプル点数によります。

回転次数比分析とは、回転機械の振動や騒音の周波数分析を行う場合、回転体に取付けたパルス発生器のパルスを外部サンプリングクロックとして、信号のサンプリングを行う方法です。

周波数分析で、1 Hzは１秒間に１周期を完了する成分です。これに対して、回転次数比分析で回転１次とは、基準とする回転体の１回転について１周期を完了する成分をいいます。
回転２次は１回転について２周期を完了する成分で、回転１次の２倍となります。このように、１回転当りの変動を基準とする分析を行うためには、回転数に同期したサンプリングを行う必要があります。、
内部サンプリングクロックそのままでは、回転速度が変化すれば１回転当りのサンプリング点数は変わってしまいますが、回転パルスに同期したクロックをサンプリングクロックとした場合には、１回転当りのサンプリング点数は常に一定となります。

例えば、600 r/minで回転している回転体を考えると、回転１次は（600 r/min）／60 ＝10 Hz、回転２次は20 Hzとなります。
回転速度が上昇して700 r/minになると、回転１次は11.7 Hz、回転２次は23.3 Hzに上がります。このように、周波数は回転速度の変化に伴って変動してしまいますが、次数として正規化すれば、回転変動による影響を受けず、ある成分に着目することも容易となります。

回転次数比分析の応用として、回転トラッキング分析があります。

回転トラッキング分析は、ある次数成分の振幅の変化を回転速度を横軸のパラメータとしてトレースすることによって、ある回転速度に対して、回転機器のどのコンポーネントが共振しているのか、あるいは回転速度の何倍（何次）の成分が共振しているのかを見極めるものです。

測定した開ループおよび閉ループ伝達関数はそれぞれ演算により閉ループ、開ループ伝達関数にすることができます。

フィードバック要素がない場合

得られた開ループ伝達関数を とすると　閉ループ伝達関数 は

得られた閉ループ伝達関数を とすると　開ループ伝達関数 は

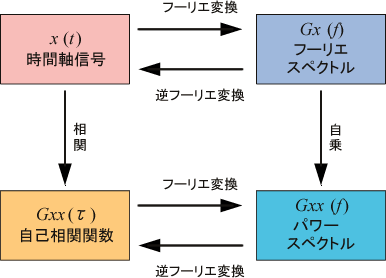
フーリエ変換と逆フーリエ変換は以下のような関係となっています。

　さらに、クロススペクトルの逆フーリエ変換は相互相関関数、周波数応答関数の逆フーリエ変換はインパルス応答となります。

フィルタに入力された信号は出力されるときに遅れを生じます。入力に対して出力信号の各周波数がどのくらいの遅れ時間をもっているのかを表したものを群遅延特性といいます。具体的には位相特性（入出力間の位相差）を角周波数で微分したもので、フィルタ回路の特性を評価する場合に用います。この特性はフィルタ回路および、周波数により値（遅延時間）が違ってきます。周波数により遅延時間が違うフィルタを用いる場合は、入力信号に対して出力信号に波形ひずみが生じてしまいます。

２つの信号 のフーリエ変換を X (f ) 、Y (f ) とし、 X (f ) の共役複素数をX^* (f ) とすれば、クロススペクトル W_xy (f ) は次式で定義されます。

クロススペクトルは２つの信号のスペクトルの、ある周波数成分どうしを掛合わせたうえで平均したもので、Ｘ軸は周波数、Ｙ軸は で表されます。クロススペクトルが、ある周波数で大きな値を示しているということは、その周波数においては２信号の周波数成分どうしの相関が大きい上に、両者の成分の大きさも大きいということを意味しています。また、クロススペクトルは、相互相関関数、伝達関数、コヒーレンス関数の計算に用いられます。

ケプストラムとは、フーリエ変換によって求められたパワースペクトルの対数値をさらにフーリエ変換したものです。ケプストラムの横軸は、ケフレンシーと呼ばれる時間の次元の値をとります。

ある系に入力される信号が周期性を持ち、その周期が長いとき、その周期が長ケフレンシー部の線ケプストラムになって現れ、基本周期として抽出することができます。また、短ケフレンシー部には、系の伝達特性を表す情報が集中し、この部分を逆フーリエ変換することにより、対数パワースペクトルのエンベロープ（包絡線）が求まります。（リフタードエンベロープ）このエンベロープは系特有のもので、入力信号のスペクトルには依存しません。

応用として、音声波、生体波などからの基本周波数およびスペクトルエンベロープの抽出などがあります。

機械振動系などで観測される振動波形には、通常、基本波成分の他に様々な高調波成分が含まれていて、伝送系に正弦波を加えると、伝送系の非線形特性などが原因で、出力信号にはひずみ成分と呼ばれる、加えた正弦波の高調波成分が現れます。そのために、このひずみに着目して、振動波形や出力信号の高調波成分を分析し、振動の特性や伝送系の忠実度などを検討することが行われます。

いま、観測波形、一般には出力波形が基本周波数 f₁ および第2高調波 f₂ 、第3高調波 f₃ 、…などの高調波成分で形成されているときのそれぞれの実効値が|Ｅ_１|、|Ｅ_２|、|Ｅ_３|、…とすれば、全体のひずみ率は

で定義されます。これを、それぞれの周波数のパワースペクトル p₁ 、p₂ 、p₃  … を用いて表すと、次のようになります。

なお、ある任意のn番目の高調波成分に注目するときには、

が使われます。

測定値は電圧値として読み取られますが、測定対象の加速度、圧力、音、などの信号の基準値が決まっていれば、電圧値を基準値に校正することにより物理量で読み取ることができます。

例１：加速度ピックアップの感度が のとき 100 mV なら 0.1 V/EU（得られた電圧値を10倍）単位を m/s² にします。

例２：マイクと音響校正器、騒音計のキャリブレートの場合は、パワースペクトルデータで、オーバーオール（ｄＢ値）を校正値になるようにします。

周波数応答関数の実数部と虚数部を周波数軸に対して別々にプロットし、これらを上下に並べて表示したものをコクアド線図といいます。固有振動数の推定等に使用できます。

コヒーレンス関数（関連度関数） は、系の入力と出力の因果関係の度合を示すもので、 は０から１の間の値をとります。 が１の場合は、その周波数において、系の出力がすべて測定入力に起因していることを示しており、 の場合、その周波数 については、系の出力は、測定入力にまったく関係ないということになります。 である場合は、測定とは無関係な信号、系内部で発生しているノイズ、系の非直線性または系の時間遅延などがあると考えられます。

はクロススペクトル、 はそれぞれｘ、ｙのパワースペクトルで、コヒーレンス関数 は平均クロススペクトルの絶対値の自乗を測定入力および系の出力の各々の平均パワースペクトルで割算したものです。

コヒーレンス関数は、その性質上平均化をしないと意味がありません。コヒーレンス関数を測定する場合は、必ず平均化を行ってください。

測定した２チャンネル間の結果のコヒーレンス関数 が小さいということは、測定結果が不正確であることを示しています。こうした不正確な部分は表示せず、 の大きい部分のみを表示する機能がコヒレンスブランキング機能です。 の値は任意に設定することができ、 の値がそれ以下の周波数では伝達関数が表示されません。

コヒーレンス関数と出力側のオートパワースペクトルとの積をコヒーレントアウトプットパワー（C.O.P.）と呼びます。

C.O.Pは、出力のオートパワースペクトルのうち測定入力に起因するオートパワースペクトルを表しています。